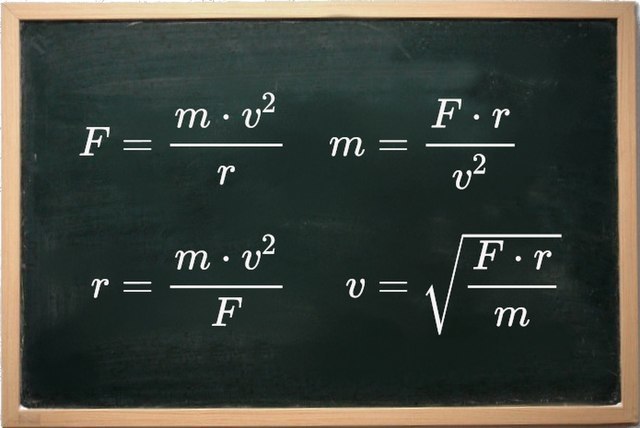B.1.1 Terme

Als Term (engl. expression) wird in der Mathematik jede Kombination aus

• Zahlen,
• Variablen (Platzhalter für Zahlen),
• Symbolen für mathematische Verknüpfungen (zum Beispiel Rechenoperationszeichen wie etwa \(+,-,\cdot,:\)) und
• Klammern

bezeichnet.

Bei der Berechnung (Auswertung) eines Terms gibt es genaue Vorrangregeln, welche Teilausdrücke zuerst zu berechnen sind („Punkt-vor-Strich-Regel“), zum Beispiel:

\[ 3+4\cdot 5^2 = 3+4\cdot 25 = 3+100 = 103 \]

Klammern haben dabei immer den höchsten Vorgang. Geklammerte Teilausdrücke sind also immer als Erstes auszuwerten. Hier ein Beispiel:

\[ 36-(4+7)\cdot 3 = 36-11\cdot 3 = 36-33 = 3 \]

Tipp: Ersetzt du eine Variable durch einen Term, verwende im Zweifelsfall immer eine Klammer!

B.1.2 Multiplizieren und Dividieren von Potenzen

Eine ganzzahlige Hochzahl (Exponent) ist eine Abkürzung für eine Multiplikation, zum Beispiel:

\[ a^5= a\cdot a\cdot a\cdot a\cdot a \]

Werden mehrere Potenzen mit gleicher Basis multipliziert, lassen sie sich zusammenfassen:

\[ a^5\cdot a^3 = a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a = a^8 \]

Der gemeinsame Exponent ist dann die Summe der einzelnen Exponenten. Allgemein gilt (\(r,s\in\mathbb{Z}\)):

\[\begin{equation} a^r\cdot a^s=a^{r+s} \tag{B.1} \end{equation}\]

Ähnliches gilt für die Division (Brüche) von Potenzen. Zum Beispiel:

\[ \frac{a^5}{a^3} = \frac{a\cdot a\cdot a\cdot a\cdot a}{a\cdot a\cdot a} = a^2 \]

Der gemeinsame Exponent ist dann die Differenz der einzelnen Exponenten. Allgemein gilt (\(r,s\in\mathbb{Z}\), \(a\ne0\)):

\[\begin{equation} \frac{a^r}{a^s}=a^{r-s} \tag{B.2} \end{equation}\]

Daraus lässt sich die Potenzdefinition um negative Potenzen erweitern:

\[\begin{equation} a^{-n} = \frac{1}{a^n} \tag{B.3} \end{equation}\]

B.1.3 Potenzieren von Produkten und Quotienten

Potenzieren wir zum Beispiel ein Produkt und wenden das Vertauschungsgesetz (Kommutativgesetz) der Multiplikation an, erhalten wir:

\[ \begin{aligned} (a\cdot b)^3 = {} & (a\cdot b)\cdot (a\cdot b)\cdot (a\cdot b) \\ = {} & (a\cdot a\cdot a)\cdot (b\cdot b\cdot b ) \\ = {} & a^3 \cdot b^3 \\ \end{aligned} \]

Allgemein gilt also:

\[\begin{equation} (a\cdot b)^n = a^n \cdot b^n \tag{B.4} \end{equation}\]

Dasselbe gilt für das Potenzieren von Quotienten (Division). Hier ein Beispiel:

\[ \left(\frac{a}{b}\right)^3 = \frac{a}{b}\cdot\frac{a}{b}\cdot\frac{a}{b} = \frac{a\cdot a\cdot a}{b\cdot b\cdot b} = \frac{a^3}{b^3} \]

Allgemein gilt also:

\[\begin{equation} \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}\qquad (\text{für }b\ne 0) \tag{B.5} \end{equation}\]

B.1.4 Potenzieren von Potenzen

Im folgenden Beispiel wird ein Ausdruck mit einer Potenz potenziert:

\[ \begin{aligned} (a^3)^2 = {} & (a^3)\cdot (a^3) \\ = {} & a\cdot a\cdot a\cdot a\cdot a\cdot a \\ = {} & a^6 \\ \end{aligned} \]

Wir können sie durch eine einzige Potenz, die der Multiplikation der beiden ursprünglichen Potenzen entspricht, ersetzen. Allgemein gilt:

\[\begin{equation} (a^m)^n = a^{m\cdot n} \tag{B.6} \end{equation}\]

B.1.5 Wurzelziehen (Radizieren) von Potenzen

Potenzieren und Wurzelziehen (Radizieren) heben einander auf, also zum Beispiel:

\[ \sqrt[2]{a^2} = a = a^1 = a^\frac{2}{2} = a^{2\cdot\frac{1}{2}} = \left(a^2\right)^\frac{1}{2} \]

Auf diese Weise lassen sich alle Wurzeln als Potenzen mit rationalen (gebrochenen) Exponenten darstellen. Allgemein gilt:

\[\begin{equation} \sqrt[n]{a^m} = a^\frac{m}{n} \tag{B.7} \end{equation}\]

Somit gelten die Potenzgesetze nicht nur für Exponenten aus den ganzen Zahlen \(\mathbb{Z}\), sondern für Exponenten aus den rationalen Zahlen \(\mathbb{Q}\). Das vereinfacht die Berechnung von Wurzelausdrücken wesentlich, da du alle schon bekannten Potenzgesetze verwenden kannst.

Hinweis: In unserem Beispiel haben wir ausdrücklich \(\sqrt[2]{\phantom{x}}\) für die Quadratwurzel geschrieben. Üblicherweise wird bei der Quadratwurzel die Zahl weggelassen, also nur \(\sqrt{\phantom{x}}\) geschrieben.

B.1.6 Multiplizieren von Termen

Sollen zwei (mehrgliedrige) Terme miteinander multipliziert werden, kommt das Distributivgesetz zum Einsatz. Jedes Glied des ersten Terms wird mit jedem Glied des zweiten Terms multipliziert. Für die Multiplikation von zwei Binomen mit den Zahlen \(a, b, c\) und \(d\) ist zum Beispiel das Ergebnis:

\[ (a+b)\cdot (c-d)=a\cdot c - a\cdot d + b\cdot c - b\cdot d \]

Achte dabei immer auf die Vorzeichen!

Fassen wir das Produkt aus zwei Zahlen als Flächeninhalt eines Rechtecks auf, lässt sich die Rechnung wie in Bild B.3 veranschaulichen.

B.1.7 Binomische Formeln

Das Quadrieren von Binomen ist ein Spezialfall des Multiplizierens von Termen. Die erste binomische Formel (Plus-Formel) lautet:

\[ \begin{aligned} (a+b)^{2}= {} & (a+b)\cdot (a+b) \\ = {} & a\cdot a+a\cdot b+b\cdot a+b\cdot b \\ = {} & a^{2}+2\cdot a\cdot b+b^{2} \\ \end{aligned} \]

Das lässt sich graphisch durch den Flächeninhalt von Rechtecken veranschaulichen (Bild B.4): Das mehrfarbige Quadrat hat die Seitenlänge \(( a + b )\). Der Flächeninhalt setzt sich aus den beiden Quadraten \(a^2\) und \(b^2\) sowie aus den zwei Rechtecken \(a\cdot b\) zusammen.

Die zweite binomische Formel (Minus-Formel) lautet:

\[ \begin{aligned} (a-b)^{2} = {} & (a-b)\cdot (a-b) \\ = {} & a\cdot a-a\cdot b-b\cdot a+b\cdot b \\ = {} & a^{2}-2\cdot a\cdot b+b^{2} \\ \end{aligned} \]

Die graphische Veranschaulichung siehst du in Bild B.5. Das weiße Quadrat mit der Seitenlänge \((a-b)\) soll aus einem großen Quadrat mit der Seitenlänge \(a\) (rot umrandetes Quadrat) entstehen. Ziehen wir zweimal das Rechteck \(a\cdot b\) (blau und grün schraffierte Flächen) von dem großen Quadrat ab, haben wir den Überlappungsbereich \(b^2\) doppelt (also einmal zu viel) abgezogen. Daher müssen wir den Flächeninhalt des kleinen gelben Quadrats (\(b^2\)) wieder einmal hinzuzählen.

Die dritte binomische Formel (Plus-Minus-Formel) schließlich ist:

\[ \begin{aligned} (a+b)\cdot (a-b) = {} & a\cdot a-a\cdot b+b\cdot a-b\cdot b \\ = {} & a^{2}-b^{2} \\ \end{aligned} \]

Die graphische Veranschaulichung siehst du in Bild B.6. Ziehst du den Flächeninhalt des Quadrats mit der Seitenlänge \(b\) von dem Flächeninhalt des Quadrats mit der Seitenlänge \(a\) ab, erhältst du die unregelmäßige Figur auf der linken Seite. Zerschneidest du die Fläche entlang der strichlierten Linie und klebst beide Teile, so wie auf der rechten Seite gezeigt, zusammen, erhältst du ein Rechteck mit den Seiten \(a-b\) und \(a-b\).

Zusammenfassung der binomischen Formeln:

\[\begin{align} (a+b)^{2} = {} & a^{2}+2\cdot a\cdot b+b^{2} \tag{B.8}\\ (a-b)^{2} = {} & a^{2}-2\cdot a\cdot b+b^{2} \tag{B.9}\\ (a+b)\cdot (a-b) = {} & a^{2}-b^{2} \tag{B.10}\\ \end{align}\]

B.1.8 Gleichungen

Eine Gleichung (engl. equation) besteht aus zwei Termen, die durch ein Gleichheitszeichen verbunden sind. Eine Gleichung drückt die zahlenmäßige Gleichheit zweier Ausdrücke aus. Zum Beispiel:

\[ 3\cdot 4 = 6 +6 \]

In den meisten Fällen kommen in einer Gleichung ein oder mehrere Platzhalter für Zahlen (Variablen, „Unbekannte“) vor. Beim Lösen einer Gleichung suchst du die Menge aller Zahlen, die, wenn du sie für die Variablen in die Gleichung einsetzt, auf beiden Seiten des Gleichheitszeichens dieselbe Zahl ergibt (Lösungsmenge). Die Gleichung ist dann erfüllt („wahre Aussage“). Zum Beispiel ist die Gleichung

\[ x^2=16 \]

für die Zahlen \(4\) und \(-4\) erfüllt. Die Lösungsmenge ist daher \(L=\{-4;4\}\).

Eine Gleichung kann als Massen auf einer Balkenwaage veranschaulicht werden (Bild B.7). So wie die Balkenwaage im Gleichgewicht bleibt, wenn du auf beiden Seiten gleiche Gewichtsstücke hinzufügst, bleibt eine Gleichung gültig, wenn du auf beiden Seiten die gleiche Rechenoperation ausführst (du erhältst eine zur ursprünglichen Gleichung äquivalente Gleichung). Diese Äquivalenzumformungen helfen dir beim Lösen von Gleichungen. Hier ein Beispiel:

\[ \begin{aligned} 4\cdot x = {} & 3 &&\qquad\Bigr\rvert\cdot \frac{1}{4} \\ (4\cdot x)\cdot\frac{1}{4} = {} & 3\cdot\frac{1}{4} \\ \frac{\cancel{4}\cdot x}{\cancel{4}} = {} & \frac{3}{4} \\ x = {} & \frac{3}{4} \\ \end{aligned} \]

B.1.9 Quadratische Gleichungen

Eine Gleichung der Form

\[\begin{equation} ax^{2}+bx+c=0\qquad (\text{für }a,b,c\in\mathbb{R}, a\ne 0) \tag{B.11} \end{equation}\]

heißt quadratische Gleichung (engl. quadratic equation). Sie hat maximal zwei Lösungen, die du mit der folgenden Lösungsformel berechnen kannst:

\[\begin{equation} x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}} \tag{B.12} \end{equation}\]

Der Ausdruck \((b^{2}-4ac)\) unter der Wurzel wird als Diskriminante \(D\) (engl. discriminant \(\Delta\)) bezeichnet. Ihr Wert entscheidet, wie viele reelle Lösungen die Gleichung besitzt:

• \(D > 0\), zwei reelle Lösungen
• \(D = 0\), eine reelle (Doppel-)Lösung, weil \(\sqrt{0}=0\) und \(\pm0\) dieselbe Zahl ergibt.
• \(D < 0\), keine reelle Lösung, weil die Wurzel einer negativen Zahl keine reelle Lösung besitzt (es gibt keine reelle Zahl, deren Quadrat eine negative Zahl ist)

Obwohl du die Lösungsformel für das Lösen jeder quadratischen Gleichung verwenden kannst, gibt es zwei Sonderfälle, bei denen du schneller zu einer Lösung kommst:

Fehlt das lineare Glied (ist also \(b=0\)), vereinfacht sich die Gleichung zu \(ax^{2}+c=0\) und du erhältst die Lösungen durch bloßes Wurzelziehen:

\[ x_{1,2}=\pm \sqrt {-c/a} \]

Fehlt das konstante Glied (ist also \(c=0\)), vereinfacht sich die Gleichung zu \(ax^{2}+bx=0\) und du kannst \(x\) herausheben und erhältst:

\[ x\cdot(ax+b)=0 \]

Ein Produkt ist genau dann null, wenn mindestens einer der beiden Faktoren null ist. Daraus ergeben sich die Lösungen:

\[ x_1=0\qquad\text{und}\qquad x_2=-b/a \]

Der Graph einer quadratischen Funktion \(f(x)=ax^{2}+bx+c\) ist eine Parabel. Die Lösungen der quadratischen Gleichung sind die Nullstellen der Funktion (Bild B.8).

Alle Computeralgebrasysteme (CAS) haben eine Funktion für das Lösen von Gleichungen. Als Beispiel siehst du die Befehle für das Lösen der Gleichung \(2t^2+t-3=0\) in unterschiedlichen Programmen:

• GeoGebra: Löse(2 t^2 + t - 3 = 0, t). Fehlt der zweite Parameter, wird automatisch \(x\) als Variable angenommen: Löse(2x^2 + x - 3 = 0)

• SageMath: solve([2*t^2 + t -3 == 0], t)

• Mathematica: Solve[2 t^2 + t - 3 == 0, t]

Links:

• Website: Gleichungen Lösen in GeoGebra
• Website: Gleichungen Lösen in SageMath
• Website: Gleichungen Lösen in Mathematica