8.8 Mehrfache Überlagerung von Schwingungen
In den 1970er-Jahren wurden sogenannte Synthesizer populär (Bild 8.41). Das sind Musikinstrumente, die auf elektronischem Wege Klänge erzeugen.
Bild 8.41: Synthesizer von 1979 (Hörprobe: Jean-Michel Jarre – Arpegiator Audio abspielen)
In diesem Kapitel erfährst du die Grundlagen für die Synthese und Analyse von Klängen.
Links:
8.8.1 Satz von Fourier
Der Grund, warum wir uns bisher ausschließlich mit harmonischen Schwingungen beschäftigt haben, ist der Satz von Fourier (engl. fourier principle), benannt nach Joseph Fourier:
Jede periodische Schwingung lässt sich als Summe von harmonischen Schwingungen erzeugen. \[\begin{equation} \begin{aligned} y(t) = A_0 + {} & A_1\cdot\sin(t) & + & B_1\cdot\cos(t) & + & \\ & A_2\cdot\sin(2\cdot t) & + & B_2\cdot\cos(2\cdot t) & + & \\ & A_3\cdot\sin(3\cdot t) & + & B_3\cdot\cos(3\cdot t) & + &\ldots \\ \end{aligned} \tag{8.17} \end{equation}\] |
Die Amplituden \(A_0, A_1, B_1, A_2, B_2, A_3, B_3,\ldots\) heißen Fourierkoeffizienten (engl. fourier coefficients). In der interaktiven Abbildung 8.42 kannst du mit den ersten Fourierkoeffizienten experimentieren und beobachten, welche Schwingung sich als Überlagerung ergibt.
Das „Nachbauen“ einer periodischen Schwingung aus harmonischen Schwingungen wird als Fourier-Synthese (engl. fourier synthesis) bezeichnet. Nach diesem Prinzip erzeugt der Synthesizer seine Klänge. In den folgenden Abschnitten findest du Beispiele für die Erzeugung einiger recht exotischer Schwingungen.
Links:
8.8.2 Synthese einer Rechteckschwingung
Eine Rechteckschwingung (engl. pulse wave) lässt sich als Summe von harmonischen Schwingungen bilden:
\[\begin{equation} y(t) = \sum_{n=1}^{\infty}\frac{1}{(2 n-1)^2}\cdot\sin((2 n-1)\cdot t) \tag{8.18} \end{equation}\]
Das Ergebnis der ersten \(n\) Summanden siehst du im interaktiven Bild 8.43.
Das blaue Diagramm in Bild 8.44 wird Frequenzspektrum genannt. Darin kannst du die zur Synthese einer Schwingung notwendigen Frequenzen und Amplituden der harmonischen Teilschwingungen ablesen.
Als Schallschwingung klingt eine Rechteckschwingung so Audio abspielen.
8.8.3 Synthese einer Sägezahnschwingung
Auch eine Sägezahnschwingung oder Kippschwingung (engl. sawtooth wave) lässt sich als Summe von harmonischen Schwingungen erzeugen:
\[\begin{equation} y(t) = \sum_{n=1}^{\infty}-\frac{1}{n}\cdot \sin(n\cdot t) \tag{8.19} \end{equation}\]
Das Ergebnis der ersten \(n\) Summanden siehst du im interaktiven Bild 8.45.
Als Schallschwingung klingt eine Sägezahnschwingung so Audio abspielen.
8.8.4 Synthese einer Dreieckschwingung
Eine Dreieckschwingung (engl. triangle wave) erhältst du durch die Summe:
\[\begin{equation} y(t) = \sum_{n=1}^{\infty}\frac{1}{(2 n-1)^2}\cdot \cos((2 n-1)\cdot t) \tag{8.20} \end{equation}\]
Das Ergebnis der ersten \(n\) Summanden siehst du im interaktiven Bild 8.46.
8.8.5 Ton, Klang und Geräusch
Sprechen Physikerinnen und Physiker von einem Ton (engl. tone), ist immer eine harmonische (sinusförmige) Schallschwingung einer einzigen Frequenz gemeint. Das einzige Instrument, dass einen Ton erzeugt, ist die Stimmgabel.
Unter einem Klang (engl. sound) verstehen Physikerinnen und Physiker eine Schallschwingung, die aus mehreren harmonischen Schallschwingungen unterschiedlicher Frequenz zusammengesetzt ist. Die Tasten und Saiten von Musikinstrumenten erzeugen daher Klänge.
Dabei wird die harmonische Schwingung mit der tiefsten Frequenz eines Klangs als Grundschwingung, alle weiteren als Oberschwingungen bezeichnet. Die Frequenz der Grundschwingung entscheidet, welche Tonhöhe wir wahrnehmen. Im Bild 8.47 siehst du links jeweils das Ort-Zeit-Diagramm der Schwingung und rechts das zugehörige Frequenzspektrum, also die Fourierkoeffizienten der Schwingung. Das Amplitudenverhältnis der Teilschwingungen ist dabei charakteristisch für ein Musikinstrument und bestimmt die sogenannte Klangfarbe (engl. timbre). Jetzt verstehst du auch, warum eine Flöte Audio abspielen und eine Geige Audio abspielen (selbst bei gleicher Tonhöhe) unterschiedlich klingen – sie erzeugen unterschiedliche Obertöne.
Bild 8.47: (a) Stimmgabel Audio abspielen (Ton), (b) Geige Audio abspielen (Klang), (c) Flöte Audio abspielen (Klang), (d) Wasserfall Audio abspielen (Geräusch)
Jede nicht-periodische Schallempfindung wird als Geräusch oder Rauschen (engl. noise) bezeichnet.
Sei bitte nicht verwirrt: In der Musik wird eine Schallempfindung, die durch eine Taste, eine Saite, etc. eines Musikinstruments erzeugt wird, als „Ton“ bezeichnet (physikalisch also ein Klang, außer bei einer Stimmgabel). Das Zusammenwirken mehrerer „Töne“ wird in der Musik als „Klang“ bezeichnet (physikalisch ebenfalls ein Klang).
Ein Synthesizer (Bild 8.41) versucht durch Überlagerung von Tönen den Klang von natürlichen Instrumenten elektronisch „nachzubauen“.
Links:
8.8.6 Fourier-Analyse
Die Umkehrung, also das Bestimmen der Fourierkoeffizienten bei einer gegebenen Schwingung, wird Fourier-Analyse (engl. fourier analysis) genannt. In Bild 8.48 siehst du das zeitliche Frequenzspektrum hintereinander gespielter Klänge als Ergebnis einer Fourier-Analyse.
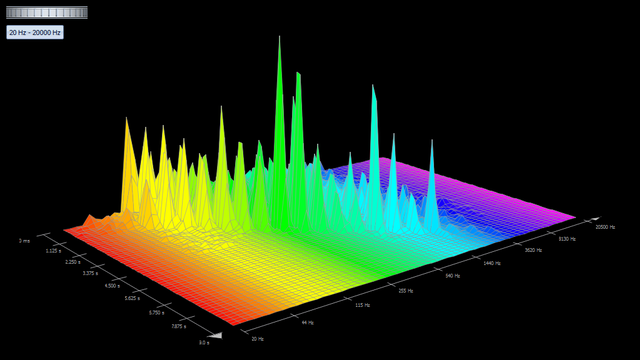
Bild 8.48: Zeit-Frequenz-Diagramm (Anhören Audio abspielen)
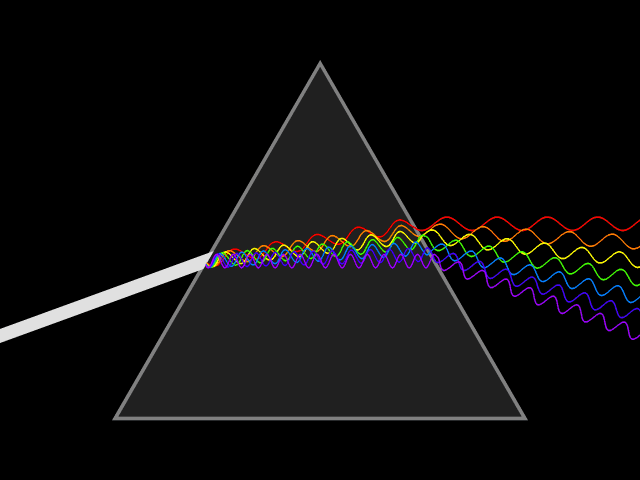
Für die Fourier-Analyse gibt es viele Anwendungsgebiete, zum Beispiel die eindeutige Stimmerkennung oder das Abspielen einer Audio-CD. Das mathematische Verfahren hinter einer Fourier-Analyse heißt Fourier-Transformation (engl. fourier transform). Was genau eine Fourier Transformation macht, lässt sich am besten mit einer Analogie zu sichtbaren Licht beschreiben. Ein weißer Lichtstrahl ist eine Mischung aus vielen Farben (Licht unterschiedlicher Frequenzen). Ein optisches Prisma (Bild 8.49, analog der Fourier Transformation) spaltet die enthaltenen Frequenzen so auf, dass sie erkennbar werden.
Links:
8.8.7 Gehör
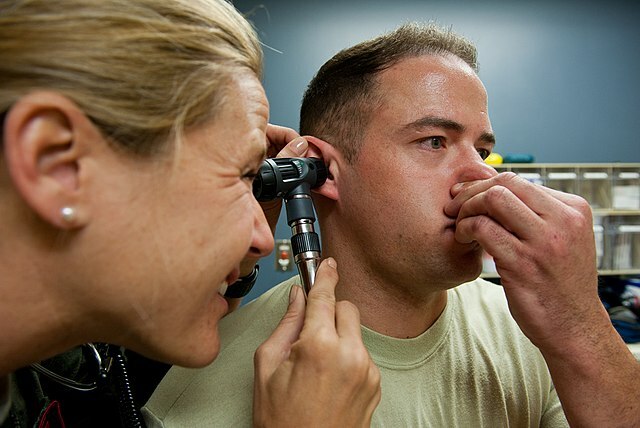
Das Gehör ist das Sinnesorgan deines Ohrs, mit dessen Hilfe du den Schall wahrnehmen kannst. Die Schwingungen einer Schallquelle (zum Beispiel einem Lautsprecher) gelangen über die Ohrmuschel und den Gehörgang, die den Schall bündeln und richten, zum Trommelfell (Bild 8.50). Diese dünne Haut überträgt die Schwingungen auf die Gehörknöchelchen – die aufgrund ihrer Form Hammer, Amboss und Steigbügel genannt werden. Die eigentliche Analyse findet in der mit Flüssigkeit gefüllten Hörschnecke (Cochlea, purpurfarbener Bereich im Bild) statt. Werden die darin befindlichen dünnen Härchen hin- und herbewegt, erzeugt das elektrische Impulse, die über den Hörnerv zum Gehirn geleitet werden.
Entlang des Schneckenkanals ist die Basilarmembran wie die Saite eines Musikinstruments über eine Länge rund \(32\;\mathrm{mm}\) gespannt. Am Anfang des Kanals – nahe dem ovalen Fenster – ist sie dick und wird gegen Ende immer dünner. Durch die zunehmende Elastizität der Membran werden an ihrem Anfang niedrige Frequenzen verstärkt, gegen Ende immer höhere Frequenzen. So können wir unterschiedliche Frequenzen unterscheiden, je nachdem, in welchem Bereich der Schnecke die Härchen bewegt werden.
Der Schall von einer seitlichen Quelle wird von beiden Ohren zeitversetzt mit unterschiedlicher Lautstärke wahrgenommen. Dadurch kann dein Gehirn auf die Richtung der Schallquelle relativ zu deinem Kopf schließen (binaurales Hören). Außerdem ist deine Ohrmuschel nicht einfach nur ein kegelförmiger Trichter. Die asymmetrische Form der Ohrmuschel bewirkt, dass eine Schallquelle, die sich vor dir befindet, ein wenig anders klingt als eine hinter dir (ebenso unter und ober dir).
Ein gesundes Ohr kann Druckänderung in der Luft von nur 20 Mikro-Pascal (\(20\;\mathrm{\mu Pa} = 20\cdot 10^{-5}\;\mathrm{Pa}\)) – das sind lediglich \(20\cdot 10^{-10}\;\mathrm{bar}\) – wahrnehmen! Es registriert Schwingung der Luft am Trommelfell, deren Amplitude kleiner als der Durchmesser eines Wasserstoffmoleküls ist. Das Ohr ist in der Lage, Schallintensitäten zu unterscheiden, deren Energie sich um das 100.000-fache unterscheidet. Das Gehör ist das empfindlichste menschliche Sinnesorgan und hat gleichzeitig den größten Wahrnehmungsbereich! Allerdings: Große Schallamplituden (zum Beispiel auch das Hören von lauter Musik) schädigen deine Sinneshärchen dauerhaft. Trage daher in lauter Umgebung immer einen Gehörschutz.
Besonders interessant ist auch noch die Eustachische Röhre. Sie verbindet den Hohlraum hinter dem Trommelfell mit dem Nasenrachenraum. Ändert sich der Druck auf das Trommelfell (zum Beispiel beim Tauchen, Bergsteigen oder Fliegen), kann mit dieser Verbindung ein Druckausgleich herbeigeführt werden (etwa durch Schlucken, Gähnen oder die Valsalva-Methode, Bild 8.51). Denn nur wenn auf beiden Seiten des Trommelfells der gleiche Druck herrscht, kann es frei schwingen.
Im Ohr befindet sich auch das Gleichgewichtsorgan. Dabei handelt es sich eigentlich um zwei getrennte Mechanismen:
Die Ohrsteine (Otolithen) befinden sich in den Vorhofsäckchen. Diese kleinen Massen liefern dem Gehirn aufgrund ihrer Trägheitsbewegung relativ zum Kopf Information über eine geradlinige Beschleunigung.
Eine klare Flüssigkeit (Endolymphe), die sich in drei annähernd kreisrunden Kanälen (den Bogengängen, Bild 8.50) über den Vorhofsäckchen befinden. Durch die unterschiedliche Ausrichtung der Bogengänge können wir bei einer Flüssigkeitsbewegung zwischen einer Drehung nach oben/unten, rechts/links und seitwärts unterscheiden.
All diese Bewegungen werden – ähnlich wie beim Hören – durch Sinneshärchen an das Gehirn gemeldet. Selbst wenn du dich nicht bewegst, drücken die Ohrsteine aufgrund der Schwerkraft unterschiedlich stark auf die Härchen und du kannst oben und unten auch mit geschlossenen Augen unterscheiden.
