12.8 Elektrische Stromkreise
Sei nicht verwirrt, dass du in Bild 12.79 einen „Wasserstromkreis“ siehst.
Du bist schon im richtigen Kapitel über elektrische Stromkreise! Hier erfährst du über die Reihenschaltung und Parallelschaltung von Verbrauchern und warum am Anfang des Kapitels ein Wasserstromkreis zu sehen ist.
Alle Schaltkreise in diesem Kapitel kannst du mit dem PhET Schaltkreis-Baukasten (virtuell) nachbauen.
12.8.1 Einfacher Stromkreis
In Bild 12.80 siehst du einen einfachen Stromkreis (engl. electrical circuit) mit einer Batterie (Spannungsquelle). Du kannst sie dir als „Elektronenpumpe“ vorstellen.
Die Pole der Spannungsquelle und ein Verbraucher („Last“) (engl. load) – in unserem Beispiel eine Lampe – sind mit Kabeln leitend verbunden und nur durch einen Schalter unterbrochen. Schließt du den Schalter, entsteht ein geschlossener Stromkreis. Die Leitungselektronen können sich jetzt von einem Pol zum anderen bewegen – es fließt ein elektrischer Strom.
Der Verbraucher hemmt die Bewegung der Ladungsträger, er leistet dem Stromfluss Widerstand. Die Bewegungsenergie der Ladungsträger wird dabei in eine andere Energieform umgewandelt, wie Licht, Wärme, Bewegung oder Schall. Ein Verbraucher oder Widerstand verringert die Stromstärke im gesamten Stromkreis! Daher ist es auch egal, an welcher Stelle in unserem Beispiel der Schalter eingebaut wird.
Die Leitungselektronen werden bei diesem Vorgang weder erzeugt noch vernichtet! Es bewegen sich nur bereits vorhandene Elektronen aufgrund der Spannung (Potenzialgefälle) von einem Pol zum anderen. In einer neuen Batterie sind gleich viele Ladungsträger wie in einer leeren Batterie!
Auch werden die Elektronen dabei nicht „verbraucht“. Durch den Ladungstransport der Elektronen von einem Pol zum anderen gleicht sich der Ladungsunterschied allmählich aus, bis schließlich die Spannung null wird und der Stromfluss zum Erliegen kommt. Die umgangssprachliche Formulierung „Die Batterie ist leer“ bedeutet, dass der Ladungsüberschuss zwischen den Polen ausgeglichen wurde.
12.8.2 Wasserstromkreis
Ein Wasserstromkreis und ein elektrischer Stromkreis sind zwar grundverschieden, trotzdem lassen sich einige Eigenschaften vergleichen. Da ein Wasserstromkreis anschaulicher ist, werden wir ihn für einige Eigenschaften als Analogie verwenden.
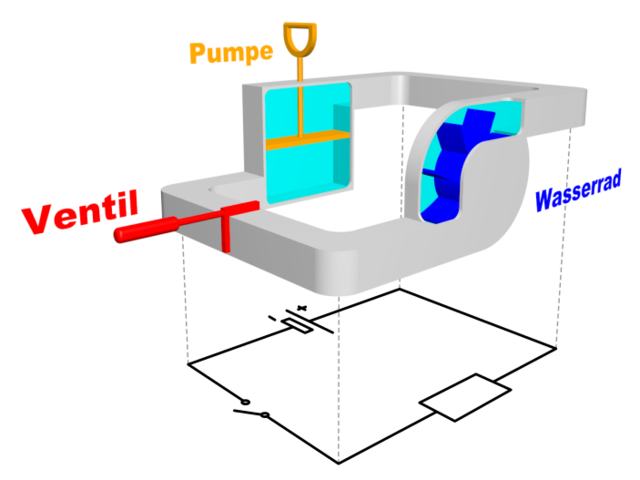
Bild 12.81: Beispiel für einen Wasserstromkreis (3D Modell)
Pumpe: Die Pumpe hebt das Wasser (erhöht die potenzielle Energie des Wassers im Gravitationsfeld). Im elektrischen Stromkreis entspricht das der Batterie, die für ein Potenzialgefälle im elektrischen Feld zwischen den Polen sorgt.
Rohre: Sie bilden ein geschlossenes System, in dem ein Wasserkreislauf stattfindet. Im elektrischen Stromkreis entspricht das dem Kabel, das die Bauteile des elektrischen Stromkreises verbindet.
Wasser: Dient als Mittler der Energie. Im elektrischen Stromkreis entspricht das den freien Ladungsträgern (Elektronen) im Leitermaterial.
Wasserrad: Nutzt die Energie des Wassers, um mechanische Arbeit zu verrichten. Im elektrischen Stromkreis entspricht das dem Verbraucher, der elektrische Energie in eine andere Energieform umwandelt.
Ventil: Kann an einer Stelle des Wasserstromkreises den Durchfluss eines Rohres unterbinden. Im elektrischen Stromkreis entspricht das einem Schalter, der den Fluss der Elektronen an dieser Stelle unterbricht. An welcher Stelle sich das Ventil befindet, ist dabei egal!
12.8.3 Serielle Schaltung von Widerständen
In Bild 12.82 siehst du einen Stromkreis mit zwei Widerständen, die hintereinanderliegen – serielle Widerstände, Widerstände in Serie oder Reihenschaltung.
Die Elektronen müssen hintereinander durch beide Widerstände und werden in jedem Widerstand in ihrer Bewegung behindert. Der Gesamtwiderstand im Stromkreis wird durch jeden weiteren seriellen Widerstand größer.
Der Gesamtwiderstand \(R_{ges}\) bei einer Reihenschaltung von Widerständen ist die Summe der Einzelwiderstände \(R_1, R_2, R_3,\ldots\) \[\begin{equation} R_{ges} = R_1 + R_2 + R_3 + \ldots \tag{12.27} \end{equation}\] |
Der Gesamtwiderstand ist größer als jeder der Einzelwiderstände.
12.8.4 Herleitung Gesamtwiderstand von seriellen Widerständen
Wählen wir zwei unterschiedliche Widerstände \(R_1\) und \(R_2\) aus gleichem Material und mit gleichem Querschnitt, gilt:
\[ R_1=\rho \cdot \frac{\ell_1}{A}\qquad\mathrm{und}\qquad R_2=\rho \cdot \frac{\ell_2}{A} \]
Setzen wir beide Widerstände zusammen, erhalten wir den Gesamtwiderstand \(R_\mathrm{ges}\). Für den zusammengesetzten Widerstand gilt (Bild 12.83):
\[\begin{align} R_\mathrm{ges} = {} & \rho \cdot \frac{\ell_1+\ell_2}{A} \notag \\ R_\mathrm{ges} = {} & \frac{\rho \cdot \ell_1+\rho \cdot \ell_2}{A} \notag \\ R_\mathrm{ges} = {} & \frac{\rho \cdot \ell_1}{A} + \frac{\rho \cdot \ell_2}{A} \notag \\ R_\mathrm{ges} = {} & R_1 + R_2 \notag \\ \end{align}\]
Der Gesamtwiderstand bei seriellen Widerständen ist die Summe aus den Einzelwiderständen.
12.8.5 Spannungsteiler
Für die folgenden Überlegungen verwenden wir das Wassermodell mit zwei seriellen Widerständen (Bild 12.84).
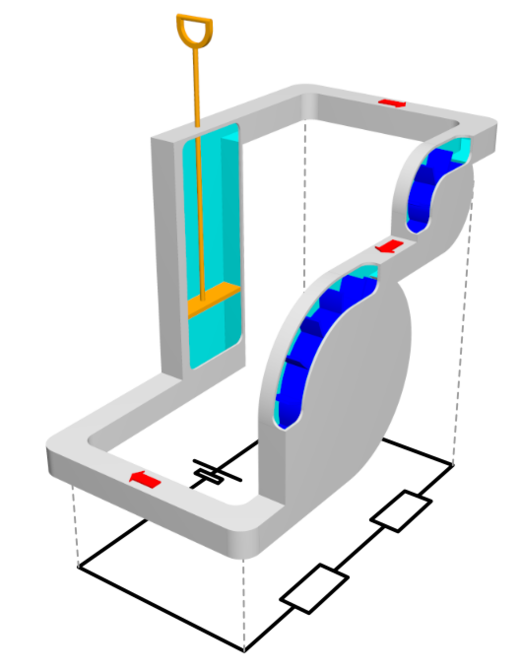
Bild 12.84: Zwei serielle Widerstände im Wasserstromkreis (3D Modell)
Da es nur einen Stromweg gibt, fließt durch alle Widerstände derselbe Strom (überall herrscht dieselbe Stromstärke) – egal, wie viele Widerstände (Gefälleabschnitte) in Serie vorkommen. Für zwei Widerstände in Serie gilt daher nach dem Ohmschen Gesetz:
\[ R_1=\frac{U_1}{I_{\mathrm{ges}}} \qquad\mathrm{und}\qquad R_2=\frac{U_2}{I_{\mathrm{ges}}} \]
Für ihr Verhältnis \(R_1:R_2\) gilt:
\[ \frac{R_1}{R_2} = \frac{\frac{U_1}{I_{\mathrm{ges}}} }{\frac{U_2}{I_{\mathrm{ges}}}} = \frac{U_1}{U_2} \]
Die Reihenschaltung von zwei Widerständen wird Spannungsteiler (engl. voltage divider) genannt. Die Spannungsabfälle stehen im selben Verhältnis wie die Widerstandswerte. \[\begin{equation} \frac{R_1}{R_2} = \frac{U_1}{U_2} \tag{12.28} \end{equation}\] |
Links:
12.8.6 Parallele Schaltung von Widerständen
In Bild 12.85 siehst du einen Stromkreis mit zwei Widerständen, die nebeneinanderliegen – parallele Widerstände.
Anders als in der seriellen Schaltung von Widerständen wird den Elektronen ein zusätzlicher Weg geöffnet. Daher können mehr Elektronen pro Zeiteinheit fließen und die Stromstärke steigt insgesamt! Größere Stromstärke bedeutet aber einen kleineren Widerstand. Der Gesamtwiderstand im Stromkreis wird durch jeden weiteren parallelen Widerstand kleiner.
Der Gesamtwiderstand \(R_{ges}\) bei der Parallelschaltung von Widerständen \(R_1, R_2, R_3,\ldots\) \[\begin{equation} \frac{1}{R_{ges}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots \tag{12.29} \end{equation}\] |
Der Gesamtwiderstand ist kleiner als jeder der Einzelwiderstände.
Um den Gesamtwiderstand für genau zwei parallele Widerstände \(R_1\) und \(R_1\) aus dieser Formel auszudrücken, gehst du folgendermaßen vor:
\[\begin{align} \frac{1}{R_\mathrm{ges}} = {} & \frac{1}{R_1} + \frac{1}{R_2}\qquad\Bigr\rvert\;(\mathrm{erweitern}) \notag \\ \frac{1}{R_\mathrm{ges}} = {} & \frac{R_2}{R_1\cdot R_2} + \frac{R_1}{R_1\cdot R_2} \notag \\ \frac{1}{R_\mathrm{ges}} = {} & \frac{R_1 + R_2}{R_1\cdot R_2} \notag \\ \end{align}\]
Und als Kehrwert:
\[\begin{equation} R_\mathrm{ges} = \frac{R_1\cdot R_2}{R_1 + R_2} \tag{12.30} \end{equation}\]
12.8.7 Herleitung Gesamtwiderstand von parallelen Widerständen
Wählen wir zwei unterschiedliche Widerstände \(R_1\) und \(R_2\) aus gleichem Material und in gleicher Länge, dann gilt:
\[ R_1=\rho \cdot \frac{\ell}{A_1}\qquad\mathrm{und}\qquad R_2=\rho \cdot \frac{\ell}{A_2} \]
Setzen wir beide Widerstände wie in Bild 12.83 parallel zusammen, erhalten wir einen neuen Widerstand \(R_\mathrm{ges}\). Für diesen zusammengesetzten Widerstand gilt:
\[\begin{align} R_\mathrm{ges} = {} & \rho \cdot \frac{\ell}{A_1+A_2} \notag \\ R_\mathrm{ges} = {} & \frac{\rho \cdot \ell}{A_1+A_2}\qquad\Bigr\rvert\; \frac{1}{(\ldots)} \notag \\ \frac{1}{R_\mathrm{ges}} = {} & \frac{A_1+A_2}{\rho \cdot \ell} \notag \\ \frac{1}{R_\mathrm{ges}} = {} & \frac{A_1}{\rho \cdot \ell} + \frac{A_2}{\rho \cdot \ell} \notag \\ \frac{1}{R_\mathrm{ges}} = {} & \frac{1}{R_1} + \frac{1}{R_2} \notag \\ \end{align}\]
Der Kehrwert des Gesamtwiderstands bei parallelen Widerständen ist die Summe aus den Kehrwerten der Einzelwiderstände. Oder mit dem Begriff der elektrischen Leitfähigkeit formuliert: Der Gesamtleitwert bei parallelen Widerständen ist die Summe der einzelnen Leitwerte.
\[ G_\mathrm{ges} = G_1 + G_2 \]
12.8.8 Stromteiler
Für die folgenden Überlegungen verwenden wir das Wassermodell mit zwei parallelen Widerständen (Bild 12.87).
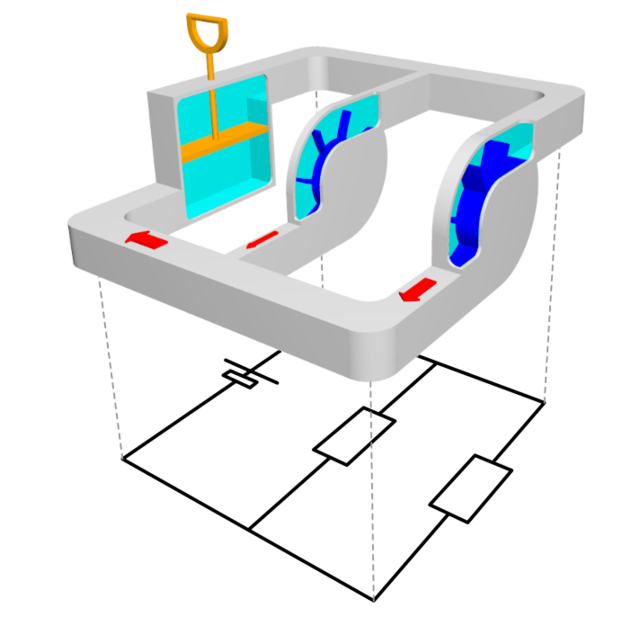
Bild 12.87: Zwei parallele Widerstände im Wasserstromkreis (3D Modell)
Die maximale Höhe im Gelände ist durch die Spannungsquelle (Pumpe) vorgegeben. Gibt es mehrere parallele Widerstände, gibt es mehrere Stromwege. Der Gesamtstrom teilt sich daher in mehrere Teilströme \(I_1, I_2,\ldots\) auf. Aber egal wie viele Teilströme vorhanden sind: Jeder Stromweg führt im Gelände von ganz oben nach ganz unten. Der Spannungsabfall ist bei allen Widerständen gleich \(U\).
Für zwei Widerstände in Parallelschaltung gilt daher nach dem Ohmschen Gesetz:
\[ R_1=\frac{U_{\mathrm{ges}}}{I_1} \qquad\mathrm{und}\qquad R_2=\frac{U_{\mathrm{ges}}}{I_2} \]
Für ihr Verhältnis \(R_1:R_2\) gilt:
\[ R_1:R_2 = \frac{U_{\mathrm{ges}}}{I_1}:\frac{U_{\mathrm{ges}}}{I_2} = \frac{\cancel{U_{\mathrm{ges}}}}{I_1}\cdot\frac{I_2}{\cancel{U_{\mathrm{ges}}}} = \frac{I_2}{I_1} \]
Die Parallelschaltung von zwei Widerständen wird Stromteiler (engl. current divider) genannt. Die Teilströme stehen im umgekehrten Verhältnis wie die Widerstandswerte. \[\begin{equation} \frac{R_1}{R_2} = \frac{I_2}{I_1} \tag{12.31} \end{equation}\] |
Auch der Strom bevorzugt „den Weg des geringsten Widerstands“, daher fließt im Zweig mit dem kleineren Widerstand der größere Strom.
Links:
12.8.9 Ermitteln des Gesamtwiderstands in einfachen Stromkreisen
Sind mehrere Verbraucher in einem Stromkreis, interessiert uns in den meisten Fällen der Gesamtwiderstand. Er gestattet es, die Gesamtstromstärke für den Stromkreis zu berechnen.
Mithilfe der Gleichungen für serielle und parallele Widerstände können wir ein kompliziertes Netzwerk aus Widerständen Schritt für Schritt zu einem einzigen Widerstand gedanklich zusammenfassen (Bild 12.88).
Dabei gehen wir – wie bei dem Auflösen von Klammern in einem mathematischen Ausdruck – von innen nach außen vor und ersetzten Widerstände durch gleichwertige Ersatzwiderstände (engl. equivalent resistance), die Strom und Spannung im restlichen Stromkreis unverändert lassen.
Zunächst fassen wir mithilfe der Gleichung (12.30) die zwei parallelen Widerstände \(R_2 =20\;\mathrm{\Omega}\) und \(R_3 =60\;\mathrm{\Omega}\) in der Mitte zu dem Ersatzwiderstand \(R_{2,3}\) zusammen.
\[ R_{2,3} = \frac{R_2\cdot R_3}{R_2 + R_3} = \frac{20\cdot 60}{20 + 60} = 15\;\mathrm{\Omega} \]
Durch die Zusammenfassung sind nur noch drei Widerstände (\(R_1 =30\;\mathrm{\Omega}\), \(R_{2,3} =15\;\mathrm{\Omega}\) und \(R_4 =40\;\mathrm{\Omega}\)) in Serie übrig (Bild 12.88, b). Der Gesamtwiderstand \(R_\mathrm{ges}\) ist daher
\[ R_\mathrm{ges} = R_1 + R_{2,3} + R_4 = 30 + 15 + 40 = 85\;\mathrm{\Omega} \]








