12.9 Verzweigte elektrische Stromkreise
In Bild 12.86 siehst du einen „Widerstandswürfel“ – ein Würfel zusammengelötet aus 12 Widerständen.
Legst du an den Diagonalecken des Würfels (siehe Pfeilpositionen) eine Spannungsquelle an, erhältst du ein Widerstandsnetzwerk, in dem die Widerstände weder parallel noch seriell liegen. Daher lässt sich der Gesamtwiderstand nicht durch die Methode des schrittweisen Zusammenfassens von Widerständen ermitteln.
In diesem Kapitel lernst du die Kirchhoffschen Gesetze kennen. Sie sind die Grundvoraussetzung, um komplizierte Stromkreise zu analysieren.
12.9.1 Knotenregel (1. Kirchhoffsches Gesetz)
Als Knoten (engl. node (junction)) in einem Stromkreis wird das Zusammentreffen von drei oder mehr Stromwegen an einem Punkt bezeichnet. In dem Stromnetzwerk in Bild 12.87 sind das genau fünf Stromwege, die sich in einem Knoten treffen.
Hast du in einem Gartenschlauch eine Verzweigung, teilen sich die Wasserteilchen auf die möglichen Wasserwege auf. Hat der Schlauch kein Loch, kannst du sicher sein, dass sich jedes der Wasserteilchen auch nach der Verzweigung irgendwo im Schlauch befindet.
Bei elektrischen Stromkreisen gilt dasselbe für die Leiter-Elektronen. Sie können nicht einfach verschwinden oder erscheinen. Jedes Elektron, das in einen Knoten hinein fließt, fließt über einen anderen Stromzweig wieder ab.
Zählen wir
- zum Knoten hinfließende Ströme positiv und
- vom Knoten wegfließende Ströme negativ,
dann können wir folgende Gleichung für die Ströme am Knoten in Bild 12.87 aufstellen:
\[ I_{1}+I_{3}-I_{2}-I_{4}-I_{5}=0 \]
Diese Gesetzmäßigkeit gilt natürlich für jeden Knoten eines Stromnetzwerks. Sie wird zu Ehren von Gustav Robert Kirchhoff die 1. Kirchhoffsche Regel oder Knotenregel (engl. Kirchhoff’s current law) genannt. Sie lautet allgemein:
Die Summe aller Ströme in einem Knoten ist null. \[\begin{equation} \sum _{{k=1}}^{n} I_k=0 \tag{12.32} \end{equation}\] |
Die Knotenregel drückt damit indirekt auch die Ladungserhaltung in einem Leiter aus.
Zwischen zwei Konten ist die Stromstärke in einem Stromzweig überall gleich groß – die Stromstärke kann sich nur bei einem Knoten ändern!
12.9.2 Maschenregel (2. Kirchhoffsches Gesetz)
Als Masche (engl. loop) in einem verzweigten Stromkreis wird jeder geschlossene Weg bezeichnet. Der Stromkreis in Bild 12.88 hat zum Beispiel die drei Maschen \(M_1\), \(M_2\) und \(M_3\). Dabei müssen wir einen Umlaufsinn festlegen. Wie wir das tun, ist egal!
Wir werden jetzt die Maschen dieses Stromkreises „abgehen“. Dazu verwenden wir wieder die Wasserstrom-Darstellung des Stromkreises (Bild 12.89).
Bild 12.89: Wasserstromkreis zu Stromkreis in Bild 12.88
Gehen wir zum Beispiel die Masche \(M_3\) ab. Wir beginnen die „Rundreise“ am Startpunkt \(S\) (und enden dort wieder). Zuerst erreichen wir den Widerstand \(R_3\) und gehen bergab (Spannungsabfall). Nach dem Knoten erreichen wir die Widerstände \(R_1\) und \(R_2\). Beide Male gehen wir bergauf (Spannungsanstieg!) und erreichen wieder den Startpunkt. Zählen wir die Spannungsabfälle negativ und die Spannungsanstiege positiv, erhalten wir am Ende unserer Rundreise null. Da wir am Ende wieder am selben Punkt angekommen sind, müssen sich alle Höhenanstiege und -abstiege ausgleichen. Die Summe ist null.
Diese Gesetzmäßigkeit gilt für alle Maschen, unabhängig davon, welche Gehrichtung wir einschlagen und auch unabhängig davon, wo wir unseren Startpunkt wählen! Diese Gesetzmäßigkeit wird zu Ehren von Gustav Robert Kirchhoff, die 2. Kirchhoffsche Regel oder Maschenregel (engl. Kirchhoff’s voltage law) genannt. Sie lautet:
Die Summe aller Spannungsabstiege und -anstiege entlang einer Masche ist null. \[\begin{equation} \sum _{{k=1}}^{n} U_k=0 \tag{12.33} \end{equation}\] |
Die Maschenregel drückt die Energieerhaltung entlang einer Masche aus.
12.9.3 Anwenden der Maschenregel
In unserem Beispiel (Bild 12.89) hast du gesehen, dass ein Widerstand nicht automatisch immer als Spannungsabfall und eine Spannungsquelle nicht immer automatisch als Spannungsanstieg zählt – es hängt immer von der Gehrichtung durch die Masche ab! Außerdem wenden wir das Ohmsche Gesetz an, um die Größe der Spannungsänderung bei einem Widerstand durch die Stromstärke auszudrücken.
In Bild 12.90 siehst du alle möglichen Fälle beim Anwenden der Maschenregel gegenüber gestellt. Die eingezeichnete Stromrichtung entspricht der technischen Stromrichtung.
- Spannungsquelle: Du gehst vom Plus- zum Minuspol. Der Pluspol liegt auf höherem Potenzial, daher kommt es zu einem Spannungsabfall \(-U\) (negativ).
- Spannungsquelle: Du gehst vom Minus- zum Pluspol. Der Minuspol liegt auf niedrigeren Potenzial, daher kommt es zu einem Spannungsanstieg \(U\) (positiv).
- Widerstand: Du gehst in Richtung des Stromes. Du beginnst daher auf höherem Potenzial, daher kommt es zu einem Spannungsabfall \(-R\cdot I\) (negativ).
- Widerstand: Du gehst gegen die Richtung des Stromes. Du beginnst daher auf niedrigerem Potenzial, daher kommt es zu einem Spannungsanstieg \(R\cdot I\) (positiv).
12.9.4 Anwendungsbeispiel: Kirchhoff Regeln
Gegeben ist der Stromkreis in Bild 12.91 mit den Spannungsquellen \(U_1=4{,}5\;\mathrm{V}\) und \(U_2=4{,}5\;\mathrm{V}\) und den Widerständen \(R_1 =1\;\mathrm{k\Omega}\), \(R_2 =100\;\mathrm{\Omega}\), \(R_3 =1\;\mathrm{k\Omega}\) und \(R_4 =470\;\mathrm{\Omega}\). Berechne die Stromstärken in allen Zweigen.
Im ersten Schritt wandeln wir die Werte von Kiloohm in Ohm um.
\[ R_1 =1\;\mathrm{k\Omega} =1000\;\mathrm{\Omega} \\ R_3 =1\;\mathrm{k\Omega} =1000\;\mathrm{\Omega} \]
Damit wir die Knotenregel anwenden können, müssen wir Stromrichtungen für die einzelnen Zweige festlegen. Da wir die tatsächlichen Stromrichtungen noch nicht kennen, legen wir für die drei Ströme \(I_1\), \(I_2\) und \(I_3\) auf zunächst beliebige Richtungen fest (Bild 12.92). Sollte sich herausstellen, dass unsere Annahme falsch war, erhalten wir eine negative Zahl für die Stromstärke. Beachte: Die Wahl der Stromrichtungen ist zwar beliebig, darf aber nach der Festlegung für den Rest der Berechnung nicht mehr verändert werden!
Unser Stromkreis hat zwei Knoten \(K_1\) und \(K_2\). Durch Anwenden der Knotenregel auf jeden Knoten erhalten wir die Gleichungen:
\[\begin{align} K_1{}:&& 0 = {} & + I_1 + I_2 + I_3 \notag \\ K_2{}:&& 0 = {} & - I_1 - I_2 - I_3 \notag \\ \end{align}\]
Wenn du dir beide Gleichungen ansiehst, wird dir vielleicht auffallen, dass beide Gleichungen äquivalent sind – du erhältst die zweite Gleichung durch Multiplizieren der ersten Gleichung mit \(-1\). Wir erhalten durch die zweite Gleichung also keine neue Information und können sie in der weiteren Rechnung weglassen.
Wenden wir jetzt die Maschenregel auf unseren Stromkreis an. Zunächst legen wir die Gehrichtungen durch die Maschen \(M_1\), \(M_2\), und \(M_3\) wie in Bild 12.93 fest (zum Beispiel im Uhrzeigersinn).
Der Einfachheit halber beginnen wir jede „Rundreise“ am Knoten \(K_1\). Mit den Regeln zur Anwendung der Maschenregel und des Ohmschen Gesetzes erhalten wir die folgenden Gleichungen:
\[\begin{align} M_1{}:&& 0 = {} & +R_3\cdot I_2 + U_1 - R_1\cdot I_1 \notag \\ M_2{}:&& 0 = {} & +R_2\cdot I_3 - U_2 + R_4\cdot I_3 - R_3\cdot I_2 \notag \\ M_3{}:&& 0 = {} & +R_2\cdot I_3 - U_2 + R_4\cdot I_3 + U_1 - R_1\cdot I_1 \notag \\ \end{align}\]
Ordnen wir die Summanden der Gleichungen,
\[\begin{align} M_1{}:&& -R_1\cdot I_1 && +R_3\cdot I_2 && && = {} & -U_1 \notag \\ M_2{}:&& && -R_3\cdot I_2 && +(R_2+R_4)\cdot I_3 && = {} & U_2 \notag \\ M_3{}:&& -R_1\cdot I_1 && && +(R_2+R_4)\cdot I_3 && = {} & U_2-U_1 \notag \\ \end{align}\]
können wir erkennen, dass die dritte Gleichung die Summe der ersten und zweiten Gleichung (\(M_3=M_1+M_2\)) ist. Die dritte Gleichung ist also schon in den zwei ersten Gleichungen enthalten und liefert keine neue Information. Auch sie kann weggelassen werden.
Durch Anwenden der Knoten- und Maschenregel auf unseren Stromkreis haben wir insgesamt drei Gleichungen für unsere drei gesuchten Teilströme erhalten.
\[\begin{align} K_1{}:&& I_1 && +I_2 && +I_3 && = {} & 0 \notag \\ M_1{}:&& -1000\cdot I_1 && +1000\cdot I_2 && && = {} & -4.5 \notag \\ M_2{}:&& && -1000\cdot I_2 && +570\cdot I_3 && = {} & 4.5 \notag \\ \end{align}\]
Durch Lösen des Gleichungssystems zum Beispiel mit dem Gaußschen Eliminationsverfahren oder mit dem GeoGebra CAS (Bild 12.94)…
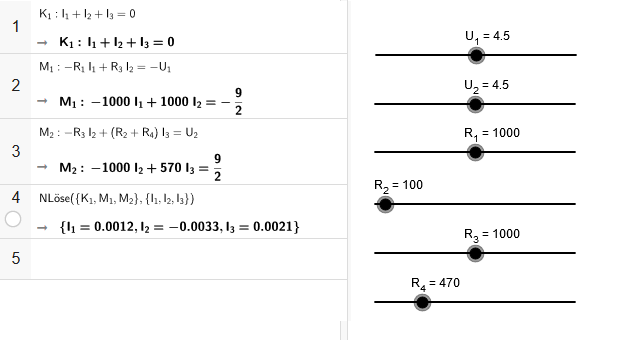
Bild 12.94: Lösung des Gleichungssystems mit GeoGebra CAS
…erhalten wir die Werte:
\[\begin{align} I_1 = {} & 0{,}0011\ldots\;\mathrm{A} \notag \\ I_2 = {} & -0{,}0033\ldots\;\mathrm{A} \notag \\ I_3 = {} & 0{,}0021\ldots\;\mathrm{A} \notag \\ \end{align}\]
An den positiven Vorzeichen der Ströme \(I_1\) und \(I_3\) siehst du, dass unsere ursprüngliche Annahme der Stromrichtungen richtig war. Nur der Strom \(I_2\) (negatives Vorzeichen) verläuft in die entgegengesetzte Richtung.
