12.5 Arbeit im elektrischen Feld
Vielleicht hast du schon einmal einen Warnhinweis wie in Bild 12.40 gesehen.
Was aber genau ist elektrische Spannung eigentlich, und was hat dieser Begriff mit dem elektrischen Feld zu tun? In diesem Kapitel untersuchen wir diesen Zusammenhang, und du erfährst, was ein elektrisches Potenzial ist und wie das elektrische Potenzialfeld und das elektrische Vektorfeld zusammenhängen.
12.5.1 Verschiebearbeit im elektrischen Feld
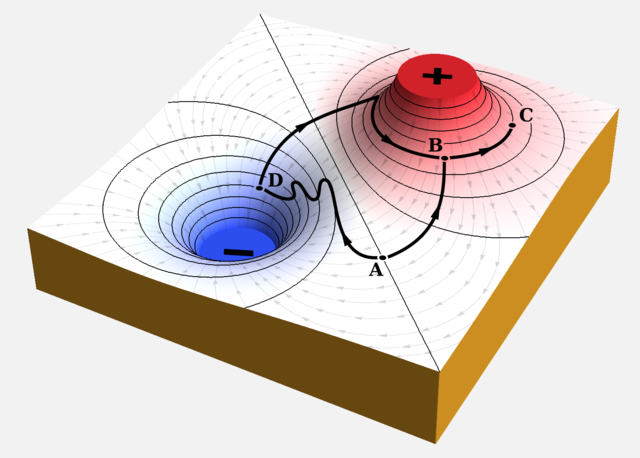
Wir beschäftigen uns zuerst mit der Verschiebearbeit einer Testladung in einem vorgegebenen elektrischen Feld. Dafür verwenden wir wieder die Geländedarstellung eines Dipolfeldes (Bild 12.41).
Legen wir einen kleinen, positiv geladenen Probekörper an eine beliebige Stelle in das elektrische Feld, sagen wir an die Stelle \(\mathrm{A}\). Verschiebst du nun die Ladung an den Punkt \(\mathrm{B}\), hast du Arbeit verrichtet. Wir bezeichnen diese Arbeit als \(W_{\mathrm{A}\rightarrow\mathrm{B}}\). Diese Arbeit hat ein positives Vorzeichen, weil du die Arbeit gegen die Feldkräfte verrichtet hast (also \(W_{\mathrm{A}\rightarrow\mathrm{B}}>0\)). Verschiebst du hingegen die Probeladung von \(\mathrm{A}\) nach \(\mathrm{D}\), verrichtet das elektrische Feld die Arbeit. Vom elektrischen Feld verrichtete Arbeiten erhalten ein negatives Vorzeichen (also \(W_{\mathrm{A}\rightarrow\mathrm{D}}<0\)).
In einem früheren Kapitel haben wir bereits gezeigt, dass die Arbeit im Gravitationsfeld wegunabhängig ist. Das Coulombsche Kraftgesetz hat dieselbe mathematische Form wie das Gravitationsgesetz. Auch das elektrische Feld ist daher ein konservatives Kraftfeld.
| Die Verschiebearbeit zwischen zwei Punkten im elektrischen Feld hängt nur von Anfangs- und Endpunkt ab, nicht aber von dem gewählten Weg – sie ist also wegunabhängig. |
Du benötigst also dieselbe Arbeit, wenn du die Ladung direkt von \(\mathrm{A}\) nach \(\mathrm{B}\) verschiebst, oder ob du den Umweg über den Punkt \(\mathrm{D}\) machst.
12.5.2 Elektrische Spannung
Nachdem du die elektrische Verschiebearbeit kennst, können wir definieren:
| Die elektrische Spannung (engl. voltage) zwischen den Punkten \(\mathrm{A}\) und \(\mathrm{B}\) in einem elektrischen Feld ist die Verschiebearbeit \(W_{\mathrm{A}\rightarrow\mathrm{B}}\) für eine positive Einheitsladung (\(+1\;\mathrm{C}\)) von \(\mathrm{A}\) nach \(\mathrm{B}\). |
Wird zur Bestimmung der Verschiebearbeit zwischen zwei Punkten eine kleine Testladung \(q\) verwendet, musst du die Verschiebearbeit noch durch ihre Ladung dividiert werden, damit du die elektrische Spannung erhältst:
Definition der elektrischen Spannung: \[\begin{equation} U_{\mathrm{A}\mathrm{B}} = \frac{W_{\mathrm{A}\rightarrow\mathrm{B}}}{q} \tag{12.14} \end{equation}\] |
Die Einheit der elektrischen Spannung ist:
\[ [U] =\frac{[W]}{[q]} =\frac{1\;\mathrm{J}}{1\;\mathrm{C}} =1\;\mathrm{V} \]
Die Einheit „Joule pro Coulomb“ wird zu Ehren von Alessandro Volta auch als Volt bezeichnet.
Im Geländemodell entspricht die elektrische Spannung dem Höhenunterschied von Anfangs- und Endpunkt.
Befinden sich Anfangs- und Endpunkt auf derselben Höhe im Gelände (zum Beispiel die Punkte \(\mathrm{B}\) und \(\mathrm{C}\)), dann ist keine elektrische Arbeit beim Verschieben einer Testladung notwendig. Die elektrische Spannung zwischen den Punkten \(\mathrm{B}\) und \(\mathrm{C}\) ist daher ebenfalls null.
12.5.3 Elektrisches Potenzial
Bisher haben wir uns im Geländemodell immer nur mit Höhenunterschieden beschäftigt. In der Geografie entspräche das den relativen Höhen(unterschieden).
Unser Ziel ist, eine gesamte „Karte des elektrischen Geländes“ anzugeben. In der Geografie wird dazu eine willkürliche Höhe (zum Beispiel der Meeresspiegel) als Bezug gewählt, und alle Höhen beziehen sich darauf - die sogenannte Meereshöhe. In Bild 12.42 siehst du den Ort Badwater Basin (Death Valley National Park, Kalifornien) der sich auf \(-85{,}5\;\mathrm{m}\) Meereshöhe – also unter dem Meeresspiegel – befindet!
Genauso gehen wir im „elektrischen Gelände“ vor, wenn wir jedem Punkt im elektrischen Feld einen Wert für die Verschiebearbeit für \(+1\;\mathrm{C}\) zuordnen.
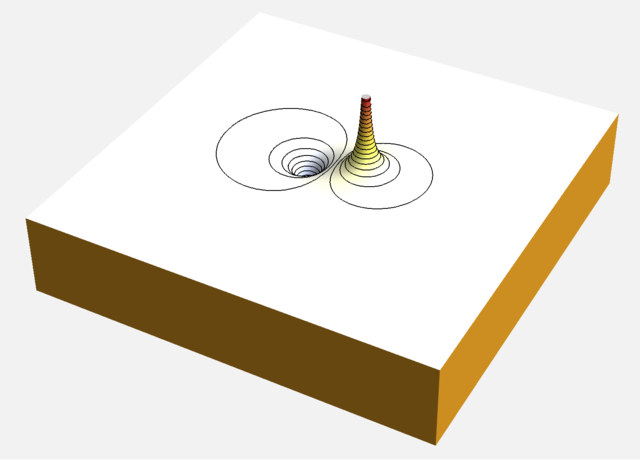
In Bild 12.43 siehst du das Gelände der weiteren Umgebung um die Ladungsanordnung. Begeben wir uns sehr weit von den felderzeugenden Ladungen weg, so befinden wir uns – egal in welche Richtung wir uns wegbewegen – auf derselben Höhe. Die Höhe dieser weit entfernten Orte – Mathematiker würden sagen „die Höhe im Unendlichen“ – bietet sich als Referenzhöhe an.
Wir definieren daher:
Das elektrische Potenzial \(\phi\) (engl. electric potential) ist die elektrische Verschiebearbeit, die benötigt wird, um eine Einheitsladung (\(+1\;\mathrm{C}\)) vom Unendlichen an den Punkt \(P\) bringen. \[\begin{equation} \phi(\mathrm{P}) =\frac{W_{\infty\rightarrow\mathrm{P}}}{q} \tag{12.15} \end{equation}\] |
Die Einheit des Potenzials ist:
\[ [\phi] =\frac{[W]}{[q]} =\frac{1\;\mathrm{J}}{1\;\mathrm{C}} =1\;\mathrm{V} \]
Also „Joule pro Coulomb“ oder Volt – dieselbe Einheit wie die der elektrischen Spannung.
Das elektrische Potenzial ist ein Skalarfeld.
12.5.4 Wahl des elektrischen Nullpotenzials
Die oben getroffene Wahl des elektrischen Nullpotenzials im Unendlichen ist sinnvoll für eine Ladungsanordnung. Da die Wahl des Nullpotenzials reine Vereinbarungssache ist, werden in der Praxis für spezielle Anwendungen auch andere Nullpotenziale gewählt:
In elektrischen Energiesystemen (zum Beispiel Elektrizitätswerken) wird üblicherweise die Erde (engl. ground) als Nullpotenzial gewählt.
In der Fahrzeugelektrik wird in Europa die metallische Karosserie als Nullpotenzial gewählt und ist leitend mit dem negativen Pol der Autobatterie verbunden. In den USA ist es üblich, den Pluspol als Nullpotenzial zu wählen.
12.5.5 Elektrische Äquipotenziale
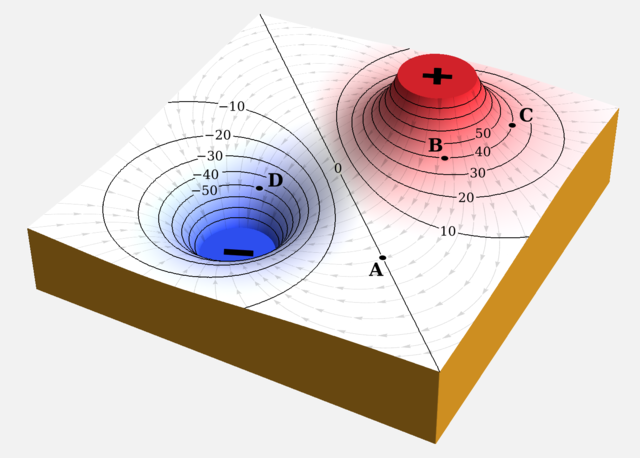
Jene Punkte, die in einem elektrischen Feld dasselbe Potenzial besitzen, liegen auf sogenannten Äquipotenzialflächen (engl. equipotential surface). In einer ebenen Felddarstellung sind sie als zweidimensionale Äquipotenziallinien zu erkennen. Sie entsprechen in der Geländedarstellung den Höhenschichtlinien (Bild 12.44).
Um durch diese Darstellung einen Eindruck von der notwendigen Verschiebearbeit zu erhalten, unterscheiden sich benachbarte Äquipotenziallinien immer um denselben Betrag. Je dichter die Äquipotenziale liegen, desto größer der Anstieg oder Abfall des Potenzials (Gradient des Potenzials).
12.5.6 Elektrische Potenzialdifferenz
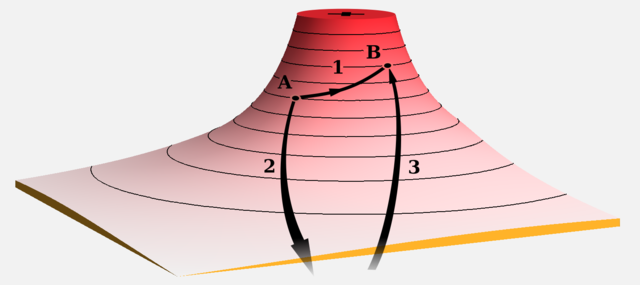
Du hast schon die elektrische Spannung und das elektrische Potenzial kennengelernt und weißt, dass beide Begriffe mit der Verschiebearbeit im elektrischen Feld zu tun haben. In Bild 12.45 siehst du wieder zwei Punkte in der Geländedarstellung.
Die elektrische Spannung \(U_{\mathrm{AB}}\) ist die Verschiebearbeit für \(+1\;\mathrm{C}\) von Punkt \(\mathrm{A}\) nach \(\mathrm{B}\) (Weg 1).
Das elektrische Potenzial \(\phi(B)\) ist die Verschiebearbeit, um eine Ladung von \(+1\;\mathrm{C}\) von sehr weit weg an den Punkt \(\mathrm{B}\) zu bringen (Weg 3).
Das elektrische Potenzial \(-\phi(A)\) (beachte das Minus!) ist die Verschiebearbeit, um eine Ladung von \(+1\;\mathrm{C}\) vom Punkt \(\mathrm{A}\) sehr weit wegzubringen (Weg 2).
Da die Verschiebearbeit wegunabhängig ist, können wir sogar einen „Umweg über das Unendliche“ machen, und wir erhalten denselben Wert für die Verschiebearbeit. Daraus folgt:
\[\begin{equation} U_{\mathrm{AB}} = \phi(B)-\phi(A) \tag{12.16} \end{equation}\]
Die Potenzialdifferenz zwischen zwei Punkten im elektrischen Feld entspricht also genau der elektrischen Spannung zwischen diesen Punkten. In der Physik werden die Begriffe elektrische Spannung und elektrische Potenzialdifferenz oft synonym verwendet. Aber Vorsicht: Wie du später sehen wirst, gilt das in induzierten Stromkreisen nicht!
12.5.7 Elektrisches Vektor- und Potenzialfeld
Sowohl das elektrostatische Vektorfeld als auch das elektrische Potenzialfeld beschreiben das elektrische Feld vollständig. Aus dem elektrischen Vektorfeld lässt sich das Potenzialfeld berechnen und umgekehrt.
Je nach Aufgabe kann es zweckmäßiger sein, das Vektorfeld oder das Skalarfeld zu verwenden. In Bild 12.46 siehst du beide Felder für einen elektrischen Dipol.
Dass die elektrischen Feldlinien und die Äquipotenziallinien immer im rechten Winkel zueinanderstehen, ist kein Zufall, sondern muss so sein. Nach der Definition der Arbeit ist diese am größten, wenn Kraft und Weg in dieselbe Richtung zeigen, also in Richtung der Feldlinie (Bild 12.47).
Die verrichtete Arbeit ist dann null, wenn Kraft und Weg im rechten Winkel zueinanderstehen. Diese Wegrichtung zeigt aber genau entlang der Äquipotentiallinien, entlang derer die Verschiebearbeit nach Definition immer null ist.
Links:
- WebApp: Ladungen und Felder
12.5.8 Elektrisches Feld der Atmosphäre
Nahe der Erdoberfläche ist eine elektrische Feldstärke von rund \(100-300\;\mathrm{V/m}\) messbar. Grund dafür ist ein elektrisches Feld, das zwischen der Erde (negativ geladen) und der Ionosphäre (positiv geladen) vorhanden ist („Schönwetterfeld“). Du kannst dir vorstellen, dass die Erdoberfläche und die Ionosphäre die Platten eines riesigen Kondensators bilden (Bild 12.48).
Je nach den Objekten und Materialien, die sich auf dem Erdboden befinden, ist die Feldstärke an unterschiedlichen Stellen verschieden groß. An leitenden, spitzen und hohen Stellen ist die Feldstärke immer am größten (liegen die elektrischen Feldlinien am dichtesten; Spitzenwirkung).
Die Erdoberfläche bildet immer eine Äquipotenzialfläche. Dieses Erdpotential wird in elektrischen Schaltungen auch nur als „Erde“ bezeichnet. Das Schaltsymbol für eine Verbindung mit dem Erdpotential siehst du in Bild 12.48 unten in der Mitte.
12.5.9 Elektronenvolt
In der Atom- und Kernphysik treten so kleine Energiewerte auf, dass es unpraktisch ist, mit der Einheit Joule zu rechnen. Stattdessen werden Energien in der Einheit Elektronenvolt (engl. electron volt) angegeben. Das ist die elektrische Energiemenge, die ein Teilchen mit einer Elementarladung (zum Beispiel ein Proton oder ein Elektron) erhält (oder abgibt), wenn es sich durch eine Potenzialdifferenz von einem Volt bewegt.
Aus dem Wert der Elementarladung folgt für das Elektronenvolt der Energiewert:
\[\begin{equation} 1\;\mathrm{eV} =1{,}6\cdot 10^{-19}\;\mathrm{C}\cdot 1\;\mathrm{V} = 1{,}6\cdot 10^{-19}\;\mathrm{J} \tag{12.17} \end{equation}\]
Hier ein Beispiel: Um das Elektron eines Wasserstoff-Atoms zu entfernen (also das Atom zu ionisieren), ist die Energiemenge von rund \(13{,}6\;\mathrm{eV}\) notwendig.