12.11 Kondensatoren
In Bild 12.113 siehst du einen Musiker mit einem ungewöhnlichen Instrument, das berührungslos gespielt wird!
Dieses elektronische Instrument heißt Theremin. Ändert sich der Abstand und die Position der Hände um das Musikinstrument, ändert sich die Lautstärke und die Tonhöhe (Hörbeispiel Audio abspielen ).
In diesem Kapitel geht es um den Kondensator, ein Bauteil in der Elektrotechnik, und seine Eigenschaften.
12.11.1 Elektrische Feldenergie
Stell dir vor, du bist die Person in Bild 12.114. Du bringst unter Kraftanstrengung und durch Verrichtung von mechanischer Arbeit zwei gleich geladene Körper einander näher.
Ging diese hineingesteckte Arbeit verloren? Lässt du die Ladungen los, bewegen sie sich beschleunigt voneinander weg. Die Arbeit war offensichtlich als potenzielle Energie irgendwo zwischengespeichert. Vergleichst du die beiden Bilder vorher (a) und nachher (b), stellst du fest, dass sich das Feldlinienbild geändert hat. Die Arbeit wurde im elektrischen Feld gespeichert. Die im elektrischen Feld gespeicherte Energie bezeichnen wir als elektrische (Feld-)Energie (engl. electrical energy).
12.11.2 Plattenkondensator
Die einfachste Bauform eines Kondensators ist der Plattenkondensator (engl. parallel-plate capacitor). Er besteht aus zwei gleich großen, parallel angeordneten, leitenden Platten. Zwischen den Platten befindet sich ein elektrischer Isolator – im einfachsten Fall Luft (Bild 12.115). Im geladenen Zustand erhältst du zwischen den Platten ein nahezu homogenes Feld.
Die elektrischen Eigenschaften eines Plattenkondensators sind abhängig von dem Plattenabstand, der Fläche der Kondensatorplatten und dem Material des Isolators.
12.11.3 Laden und Entladen eines Kondensators
In Bild 12.116 siehst du einen einfachen Stromkreis mit einer Batterie (links), einem Kondensator (Mitte) und einem Verbraucher (Widerstand, rechts).
Verwenden wir die Schalterstellung (a), werden Batterie und Kondensator miteinander verbunden. Die Batteriespannung sorgt dafür, dass Leiterelektronen von einer Seite auf die andere wandern. Es fließt ein Ladestrom und der Kondensator wird geladen.
Befindet sich auf der einen Seite des Kondensators die Ladungsmenge \(Q\), befindet sich auf der gegenüberliegenden Platte die gleich große Ladung \(-Q\). Zwischen den Platten entsteht ein homogenes Kondensatorfeld. Dieses Feld ist aber der Batteriespannung entgegengesetzt! Mit jeder Ladung, die auf die Platte aufgebracht wurde, erhöht sich die Arbeit, die nötig ist, eine weitere Ladung auf den Kondensator zu verschieben.
Der Stromfluss kommt zum Erliegen, sobald die Batteriespannung und die Spannung zwischen den Kondensatorplatten entgegengesetzt gleich groß sind. Der Kondensator ist jetzt vollständig geladen. Im Bild 12.117 siehst du den Verlauf der Kondensatorspannung und des Ladestroms im Bereich bis zum Zeitpunkt \(x\). Beachte den nicht linearen Verlauf der Kurven!
Ändern wir die Schalterstellung auf (b), wird der Kondensator von der Batterie getrennt und mit dem Verbraucher verbunden. Jetzt gibt es keine Batteriespannung mehr, die den Ladungsunterschied zwischen den Platten aufrecht hält, und der Ladungsunterschied zwischen beiden Seiten des Kondensators beginnt sich auszugleichen. Dabei fließt ein Entladestrom über den Verbraucher (Bild 12.117 ab dem Zeitpunkt \(x\)). Der Kondensator ist jetzt selbst eine Spannungsquelle geworden. Die dafür nötige Energie war im elektrischen Feld des Kondensators gespeichert.
In unserem Beispiel sind die Zeiten für den Lade- und Entladevorgang ungefähr gleich lang. Das muss aber nicht so sein. Ein Kondensator kann auch sehr langsam geladen und dann schnell entladen werden (zum Beispiel in einem Blitzgerät) und umgekehrt.
12.11.4 Verschiebearbeit in einem homogenen Feld
In einem homogenen Feld eines Plattenkondensators ist die Verschiebearbeit besonders einfach zu berechnen, da die Feldstärke (und die elektrische Kraft) an jeder Stelle im Feld gleich groß ist.
Wir möchten eine Ladung \(q\) gegen die Feldkraft von einer Kondensatorplatte zur gegenüberliegenden Kondensatorplatte verschieben, wobei die Platten im Abstand \(d\) voneinander entfernt sind (Bild 12.118). Die physikalische Arbeit ist definiert als:
\[ W = F\cdot s \]
Für unseren Fall sind Kraft- und Wegrichtung gleich, daher gilt:
\[ W_\text{K} = F_C\cdot d \]
Mit der Definition der elektrischen Feldstärke \(E=F_C/q\) folgt daraus:
\[ W_\text{K} = F_\text{C}\cdot d = (q\cdot E)\cdot d = q\cdot E\cdot d \]
Und wir erhalten die gesuchte Verschiebearbeit der Ladung \(q\).
Für die Spannung zwischen den Kondensatorplatten gilt daher:
\[\begin{equation} U_\text{K} = \frac{W_\text{K}}{q} = \frac{q\cdot E\cdot d}{q} = E\cdot d \tag{12.34} \end{equation}\]
12.11.5 Gespeicherte Ladung eines Plattenkondensators
Wie viel Ladung bei einer angelegten Spannung auf einem Plattenkondensator gespeichert wird, ist von seiner Geometrie abhängig.
Setzen wir in der Formel für die Spannung zwischen den Kondensatorplatten (12.34) die Formel für die Feldstärke im Kondensatorfeld ein, erhalten wir:
\[\begin{align} U_\text{K} = {} & E\cdot d \notag \\ = {} & \frac{Q}{\varepsilon_0\cdot A}\cdot d \notag \\ = {} & \frac{d}{\varepsilon_0\cdot A}\cdot Q \tag{12.35} \\ \end{align}\]
Aus dieser Gleichung sehen wir, dass (bei gleicher Spannung) umso mehr Ladung auf den Kondensatorplatten gespeichert werden kann,
- je kleiner der Plattenabstand \(d\)
- je größer die Fläche der Kondensatorplatten \(A\)
ist. Ein kleiner Plattenabstand ist also günstig für den Bau eines Plattenkondensators, allerdings gilt auch: Je kleiner der Plattenabstand, desto früher kommt es zu einer Blitzendladung zwischen beiden Platten.
Bringen wir die Ladung auf die andere Seite der Gleichung, sehen wir etwas Interessantes:
\[\begin{align} U_\text{K} = {} & \frac{d}{\varepsilon_0\cdot A}\cdot Q &&\qquad\Bigr\rvert\cdot \frac{1}{Q} \notag \\ \frac{U_\text{K}}{Q} = {} & \frac{d}{\varepsilon_0\cdot A} = \text{const} \notag \\ \end{align}\]
Auf der rechten Seite der Gleichung befinden sich nur Größen, die von den Eigenschaften des Plattenkondensators abhängig sind. Für einen konkreten Kondensator ist der Plattenabstand \(d\) und die Plattengröße \(A\) normalerweise unveränderlich, und damit ist dieser Ausdruck konstant. Damit muss aber auch die linke Seite der Gleichung – das Verhältnis aus Kondensatorspannung \(U_\text{K}\) und aufgebrachter Ladungsmenge \(Q\) – für einen Kondensator immer konstant sein!
12.11.6 Kapazität eines Kondensators
Als Kapazität \(C\) (engl. capacitance) eines Kondensators ist das konstante Verhältnis von aufgebrachter Ladungsmenge \(Q\) und Kondensatorspannung \(U_\text{K}\) festgelegt:
| \[\begin{equation} C = \frac{Q}{U_\text{K}} \tag{12.36} \end{equation}\] |
Die Einheit der Kapazität ist:
\[ [C] = \frac{[Q]}{[U_\text{K}]} = \frac{1\;\mathrm{C}}{1\;\mathrm{V}} = 1\;\mathrm{F} \]
Die Einheit „Coulomb pro Volt“ wird zu Ehren von Michael Faraday auch Farad genannt. Das Farad ist eine sehr große Einheit. Bauteile besitzen üblicherweise Kapazitäten von Mikrofarad (\(\mathrm{\mu F}\)) oder sogar nur Picofarad (\(\mathrm{pF}\)). Die Angabe der Kapazität eines Kondensators (Kenngröße) befindet sich entweder auf dem Bauteil selbst oder im Datenblatt des Herstellers.
Vorsicht Verwechslungsgefahr: Im Themenbereich Kondensator findest du das große „C“ sowohl als Formelsymbol für die Kapazität (\(C\)), als auch für die Einheit der Ladung (\(\mathrm{C}\))!
Lass dich durch das Wort „Kapazität“ nicht verwirren. Du darfst dir darunter nicht ein konkretes Fassungsvermögen vorstellen. Je größer die Spannung, desto mehr Ladung wird auf die Platten verteilt. Es ist wie bei einer Flasche, in der immer mehr Luftteilchen gespeichert werden, je größer der Druck wird. Früher oder später wird die Flasche dann bersten. Analog ist es die Durchschlagspannung, die zweite Kenngröße eines Kondensators, die die maximal mögliche gespeicherte Ladung beschränkt.
Aus Gleichung (12.35) folgt für die Kapazität eines Plattenkondensators mit der Fläche \(A\) und dem Plattenabstand \(d\) der Zusammenhang:
\[ C = \frac{Q}{U_\text{K}} = \frac{\varepsilon_0\cdot A}{d} \]
12.11.7 Gespeicherte Energie eines Kondensators
Wenn wir einen Kondensator als Spannungsquelle verwenden möchten, interessiert uns vor allem, wie viel Energie in ihm gespeichert ist.
Die elektrische Feldenergie eines geladenen Kondensators ist: \[\begin{equation} E_{el} = \frac{C\cdot U^2}{2} \tag{12.37} \end{equation}\] |
In dieser Formel bedeuten:
- \(E_{el}\), die im Kondensator gespeicherte elektrische Energie (in \(\mathrm{J}\))
- \(C\), die Kapazität des Kondensators (in \(\mathrm{C}/\mathrm{V}\))
- \(U\), die am Kondensator angelegte Spannung (in \(\mathrm{V}\))
12.11.8 Herleitung der Energie eines Kondensators
Beginnen wir mit einem ungeladenen Kondensator und bringen ein Leiterelektron nach dem anderen auf die andere Seite, so erhalten wir einen geladenen Kondensator. Die für diese Ladungstrennung verrichtete Arbeit entspricht exakt der im Kondensatorfeld gespeicherten elektrischen Energie.
Die Spannung hast du als die Verschiebearbeit für eine positive Einheitsladung (\(1\;\mathrm{C}\)) kennengelernt. Verschiebst du eine Ladungsmenge von \(Q\) Coulomb bei einer konstanten Spannung \(U\), ist die Arbeit daher \(W=Q\cdot U\). Diese Arbeit ist im U-Q-Diagramm als der rechteckige Flächeninhalt unter der konstanten Spannungskurve zu erkennen (Bild 12.119 links).
Beim Laden eines Kondensators sieht die Sache anders aus. Denn mit jeder aufgebrachten Ladung erhöht sich die Spannung zwischen den Kondensatorplatten. Die Spannung nimmt linear mit der gespeicherten Ladung zu. Im U-Q-Diagramm ist die Spannungskurve eine Gerade mit der Steigung \(1/C\), mit \(C\) der Kapazität des Kondensators (Bild 12.119 rechts). Die gespeicherte Energie entspricht in diesem Fall dem Flächeninhalt der Dreiecksfläche unter der Kurve.
\[ W=\frac{1}{2}\cdot U\cdot Q \]
Drücken wir die aufgebrachte Ladungsmenge durch die Kapazität des Kondensators aus \(Q=C\cdot U\), erhalten wir:
\[\begin{align} W = {} & \frac{1}{2}\cdot U\cdot Q \notag \\ = {} & \frac{1}{2}\cdot U\cdot (C\cdot U) \notag \\ = {} & \frac{1}{2}\cdot C\cdot U^2 \notag \\ \end{align}\]
12.11.9 Parallelschaltung von Kondensatoren
Für die Gesamtkapazität \(C_\mathrm{ges}\) von \(n\) parallel geschalteten Kondensatoren (12.120) mit den Kapazitäten \(C_1\), \(C_2\),… \(C_n\) gilt:
| \[\begin{equation} C_\mathrm{ges} = C_1 + C_2 + \ldots + C_n \tag{12.38} \end{equation}\] |
Die Gesamtkapazität steigt daher mit jedem weiteren parallel geschalteten Kondensator.
12.11.10 Herleitung Parallelschaltung von Kondensatoren
Werden zwei Plattenkondensatoren parallel geschaltet, (Bild 12.121) erhöht sich die Gesamtfläche und die Kondensatoren wirken wie ein einziger Kondensator mit der Fläche \(A_1+A_2\).
Da die Kapazität eines Plattenkondensators proportional zur Fläche ist, erhöht sich die Gesamtkapazität. Die Gesamtkapazität der Kondensatoren beträgt
\[\begin{align} C_\mathrm{ges} = {} & \frac{\varepsilon_0\cdot (A_1+A_2)}{d} \notag \\ = {} & \frac{\varepsilon_0\cdot A_1 + \varepsilon_0\cdot A_2}{d} \notag \\ = {} & \frac{\varepsilon_0\cdot A_1}{d} + \frac{\varepsilon_0\cdot A_2}{d} \notag \\ = {} & C_1 + C_2 \notag \\ \end{align}\]
Damit lässt sich die Gesamtkapazität als Summe der Kapazitäten der einzelnen parallel geschalteten Kondensatoren ausdrücken. Auf die gleiche Weise lässt sich das Ergebnis auf mehr als zwei Kondensatoren verallgemeinern.
In der Herleitung haben wir Plattenkondensatoren verwendet. Das Ergebnis ist aber allgemein für alle Arten von Kondensatoren gültig.
12.11.11 Serielle Schaltung von Kondensatoren
Für die Gesamtkapazität \(C_\mathrm{ges}\) von \(n\) seriell geschalteten Kondensatoren (12.122) mit den Kapazitäten \(C_1\), \(C_1\),… \(C_n\) gilt:
| \[\begin{equation} \frac{1}{C_\mathrm{ges}} = \frac{1}{C_1} + \frac{1}{C_2} + \ldots + \frac{1}{C_n} \tag{12.39} \end{equation}\] |
Die Gesamtkapazität sinkt daher mit jedem weiteren in Serie geschalteten Kondensator.
12.11.12 Herleitung serielle Schaltung von Kondensatoren
Werden zwei Plattenkondensatoren in Serie geschaltet (Bild 12.123), liegen die zwei Platten in der Mitte (untere Platte des ersten Kondensators und die obere Platte des zweiten Kondensators) am selben Kabel. Alle Stellen am selben Kabel haben aber immer dasselbe Potenzial und daher müssen auch diese beiden Platten dasselbe Potenzial haben – oder anders ausgedrückt: Die Spannung zwischen diesen beiden Platten ist null. Daher können die Platten in der Mitte entfallen und die beiden Kondensatoren in Serie verhalten sich wie ein einziger Kondensator mit dem Plattenabstand \(d_1+d_2\).
Da die Kapazität eines Plattenkondensators indirekt proportional zum Plattenabstand ist, wird die Gesamtkapazität kleiner. Sie lautet:
\[ C_\mathrm{ges} = \frac{\varepsilon_0\cdot A}{d_1+d_2} \]
Bilden wir davon den Kehrwert, erhalten wir die Gleichung:
\[\begin{align} \frac{1}{C_\mathrm{ges}} = {} & \frac{d_1+d_2}{\varepsilon_0\cdot A} \notag \\ \frac{1}{C_\mathrm{ges}} = {} & \frac{d_1}{\varepsilon_0\cdot A} + \frac{d_2}{\varepsilon_0\cdot A} \notag \\ \frac{1}{C_\mathrm{ges}} = {} & \frac{1}{C_1} + \frac{1}{C_2} \notag \\ \end{align}\]
Damit lässt sich der Kehrwert der Gesamtkapazität als Summe der Kehrwerte der Kapazitäten der einzelnen in Serie geschalteten Kondensatoren ausdrücken. Auf die gleiche Weise lässt sich das Ergebnis auf mehr als zwei Kondensatoren verallgemeinern.
In der Herleitung haben wir Plattenkondensatoren verwendet. Das Ergebnis ist aber allgemein für alle Arten von Kondensatoren gültig.
12.11.13 Kondensator mit Dielektrikum
Bisher sind wir immer davon ausgegangen, dass sich zwischen den Kondensatorplatten Luft (oder Vakuum) befindet. Ist der Zwischenraum mit einem elektrischen Isolator gefüllt, einem sogenannten Dielektrikum (engl. dielectric), erhöht sich dadurch die Kapazität des Kondensators. Das griechische Wort dia bedeutet „durch“ und dielectrium bedeutet so viel wie „Material, das vom elektrischen Feld durchsetzt wird“.
Durch elektrische Polarisation bildet sich im Dielektrikum ein zum äußeren Feld entgegen gerichtetes elektrisches Feld. Das Gesamtfeld wird dadurch geschwächt (Bild 12.124 b) und mehr Ladungen können bei gleicher Spannung auf die Platten aufgebracht werden.
Für die Kapazität eines Plattenkondensators mit Dielektrikum gilt:
\[ C = \varepsilon_r\cdot C_\mathrm{Vakuum} = \varepsilon_r\cdot \frac{\varepsilon_0\cdot A}{d} \]
Die dimensionslose Zahl \(\varepsilon_r\) wird Permittivitätszahl (von lat. permittere erlauben, zulassen), eines Dielektrikums genannt. Sie gibt die Erhöhung der Kapazität eines Kondensators durch ein Dielektrikum an und ist für alle Stoffe größer Eins (\(\varepsilon_\mathrm{r}>1\)). Ihr konkreter Wert für einen bestimmten Stoff kann in Materialtabellen nachgeschlagen werden. Porzellan beispielsweise hat eine Permittivitätszahl von \(\varepsilon_r \approx 7\) und Wasser – aufgrund der starken elektrischen Polarisation – einen wesentlich größeren Wert von \(\varepsilon_r \approx 80\).
Ein ähnlich lautender Begriff ist die Permittivität \(\varepsilon\) eines Stoffes. Damit wird das Produkt aus der Permittivitätszahl des Stoffes und der elektrischen Feldkonstante bezeichnet.
\[ \varepsilon =\varepsilon_\mathrm{r}\cdot \varepsilon_0 \]
Das Theremin, das du am Kapitelanfang kennengelernt hast, ist wie ein Kondensator aufgebaut. Die Hand bildet dabei das Dielektrikum. Wird das Dielektrikum (also die Hand) aus dem Kondensator entfernt, sinkt die Kapazität und damit – bei gleicher Ladung – steigt die elektrische Spannung und umgekehrt. Diese Spannungsschwankungen werden dann als Tonhöhe (rechte Hand) und Lautstärke (linke Hand) hörbar gemacht.
12.11.14 Durchschlagspannung
Erhöhen wir bei einem Plattenkondensator die Spannung immer weiter, wird die Feldstärke so groß, dass die Luft zwischen den Platten leitend wird. Der Plattenkondensator entlädt sich schlagartig durch einen Blitz. Ähnliches passiert, wenn der Zwischenraum mit einem Dielektrikum gefüllt ist. Übersteigt die angelegte Spannung einen bestimmten Wert, werden durch die hohe Feldstärke im Kondensator einzelne Elektronen aus dem Dielektrikum herausgerissen und das Isolator-Material wird elektrisch leitend.
Bei diesem Durchschlag (engl. dielectric breakdown) wird das Dielektrikum in den meisten Fällen dauerhaft beschädigt und muss ersetzt werden (Bild 12.125).
Die Durchschlagspannung (engl. breakdown voltage) eines Kondensators begrenzt daher die maximale Ladung und ist neben der Kapazität die zweite Kenngröße eines Kondensators.
12.11.15 Unterschiedliche Bauformen von Kondensatoren
In Bild 12.126 siehst du einige Bauformen von Kondensatoren mit unterschiedlicher Kapazität und Durchschlagspannung.
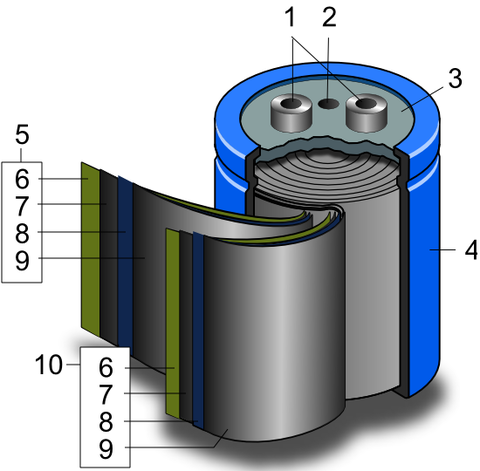
Eine übliche Bauform eines Kondensators ist der sogenannte Wickelkondensator. Dabei werden 4 Streifen (Leiter-Dielektrikum-Leiter-Isolator) übereinandergelegt und zu einem Zylinder zusammengerollt (Bild 12.127). Auf diese Weise wird eine große Fläche bei kompakter Bauweise erreicht.
Normale Kondensatoren sind symmetrisch und können von beiden Seiten geladen werden. Eine Sonderform ist der Elektrolytkondensator („Elko“), der immer von derselben Seite beladen werden muss. Er unterscheidet sich daher auch im Schaltbild von einem gewöhnlichen Kondensator (Bild 12.128).
12.11.16 Mechanische Analogie zu einem Kondensator
In Bild 12.129 siehst du eine mechanische Analogie zu einem Kondensator: Ein Wasserrohr, das an einer Stelle mit einer Gummi-Membran versiegelt ist.
Die Wassermoleküle können zwar die Membran nicht durchdringen, aber die Membran dehnt sich und lässt einen gewissen Wasserstrom zu. Analog einem Kondensator, bei dem es zu einem kurzfristigen Lade- und Entladestrom kommt.
Je mehr eine Membran gedehnt wird, desto mehr drückt sie auf das Wasser zurück. Sind beide Drücke gleich groß, kommt es zu keinem weiteren Stromfluss mehr. Analog gibt es keinen elektrischen Stromfluss mehr, wenn die Batteriespannung und die Spannung zwischen den Kondensatorplatten entgegengesetzt gleich groß sind.
Ist der Wasserdruck zu groß, reißt die Membran und Wasser kann ungehindert durch das Rohr fließen. Analog kommt es bei zu großer Spannung bei einem Kondensator zu einem elektrischen Durchschlag, bei dem das Dielektrikum leitend wird und der Kondensator zerstört wird.
Die Dehnbarkeit der Membran beschreibt, wie viele Wasserteilchen bei einem bestimmten Wasserdruck wandern können. Analog beschreibt die Kapazität eines Kondensators, wie viel Ladung sich bei einer bestimmten Batteriespannung auf den Kondensatorplatten befindet.
Ein aufgeladener Kondensator speichert elektrische Energie, analog zu der potentiellen Energie einer gedehnten Membran oder gespannten Feder. Diese Analogie drückt sich auch in den Formeln für die gespeicherte Energie eines Kondensators und einer gespannten Feder aus:
\[\begin{align} E = {} & \frac{C\cdot U^2}{2} && \text{Kondensator} \notag \\ E = {} & \frac{k\cdot x^2}{2} && \text{Schraubenfeder} \notag \\ \end{align}\]
12.11.17 Batterie oder Kondensator
Sowohl in einer Batterie als auch in einem Kondensator wird elektrische Energie gespeichert. Im Gegensatz zur Batterie, die Energie chemisch speichert, befindet sich beim Kondensator die Energie im elektrischen Feld.
Momentan ist die Speicherdichte – daher wie viel elektrische Energie pro Volumen gespeichert werden kann – von Batterien noch größer als die von Kondensatoren. Wo es auf die Menge der gespeicherten Energie ankommt (zum Beispiel in Smartphones oder einem Elektroauto), wird daher eine Batterie oder ein Akku als Energiespeicher verwendet.
Chemische Reaktionen benötigen Zeit, deswegen entlädt sich eine Batterie wesentlich langsamer als ein Kondensator. Wird die elektrische Energie rasch benötigt (zum Beispiel einem Blitzgerät), wird ein Kondensator als Speicher verwendet.

Bild 12.130: Kondensatorbaum des Fermilab
In Bild 12.130 siehst du den „Kondensatorbaum“ eines Forschungszentrums für Teilchenphysik. Diese Anlage speichert die Energie von \(8\cdot 10^{-8}\;\mathrm{J}\). Du wirst jetzt vielleicht denken „das ist ja unglaublich wenig Energie“. Stimmt! Aber die Anlage kann diese Energie in nur \(2\cdot 10^{-16}\;\mathrm{s}\) bereitstellen. Das ergibt eine Leistung von unglaublichen \(360\;\mathrm{MW}\) (siehe Datenblatt)!
Die Menge an gespeicherter Energie hängt entscheidend von der Größe der Oberfläche eines Kondensators ab. Je zerklüfteter die Oberfläche, desto mehr Energie lässt sich in einem Volumen speichern. Durch Nanotechnologie gelingt es immer kleinere Strukturen herzustellen. In Zukunft kann es durchaus sein, dass Kondensatoren mit gleicher oder sogar größerer Speicherdichte als Batterien gebaut werden können.