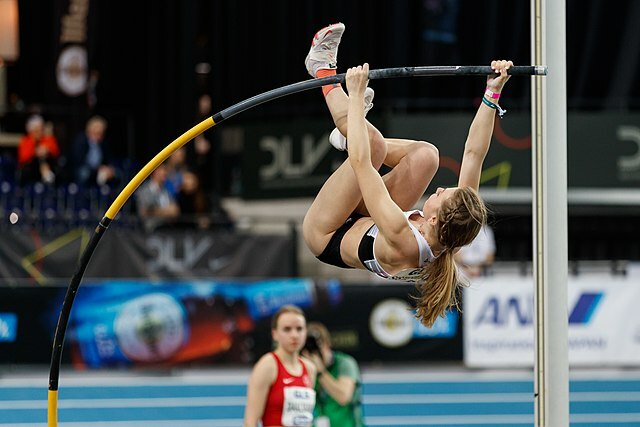5.3 Energie
So wie Arbeit ist auch Energie ein alltäglicher Begriff. Ob in „Energiedrink“, „energiegeladen“, „Energiewende“, „Energiesparen“ oder „Energiehaushalt“ in all diesen Begriffen steckt das Wort Energie.
In diesem Kapitel geht es um den Energie-Begriff in der Physik.
5.3.1 Was ist Energie?
Richard Feynman sagte in seinen Vorlesungen: „Es ist wichtig, einzusehen, dass wir in der heutigen Physik nicht wissen, was Energie ist.“ Daran hat sich bis heute nichts geändert. Obwohl wir Energie in unseren Überlegungen und Rechnungen verwenden und uns der Energiebegriff in allen Bereichen der Physik begegnet, ist eine exakte Definition sehr schwierig. Dass wir ihn trotzdem erfolgreich verwenden können, liegt an der engen Verwandtschaft zum Begriff der (physikalischen) Arbeit. Hier ein paar Beispiele:
Ziehst du eine Armbanduhr auf, verrichtest du Verformungsarbeit an einer Spiralfeder. Wenn du damit fertig bist, ist die von dir verrichtete Arbeit aber nicht verloren. Sie sorgt dafür, dass die Uhr die nächsten Tage funktioniert. Du könntest also sagen, die zuvor verrichtete Arbeit ist irgendwie in der gespannten Feder gespeichert.
Bei einer Kuckucksuhr ist es ähnlich. Dort ziehst du die Uhr mit einem Gewicht auf. Die verrichtete Hubarbeit ist irgendwie in den Gewichten gespeichert und sorgt dafür, dass die Uhr die nächsten Tage funktioniert.
Beim Stabhochsprung musst du beim Anlauf zunächst Beschleunigungsarbeit verrichten. Sobald der Stab in den Einstichkasten fällt, beginnt er sich zu verformen und du wirst langsamer. Die Arbeit beim Anlauf ist aber nicht verloren, denn der Stab hebt dich gegen die Schwerkraft nach oben und verrichtet Hubarbeit (Bild 5.15). Die Arbeit war also im Stab irgendwie gespeichert.
Wurde an einem Körper Arbeit verrichtet, können wir in vielen Fällen diese Arbeit zu einem späteren Zeitpunkt wieder abrufen. Wir sprechen dann von Energie (engl. energy) um auszudrücken, dass diese Arbeit nicht verloren gegangen ist, sondern irgendwo „zwischengespeichert“ war. Eine vorläufige Definition von Energie kann daher lauten:
| Energie ist gespeicherte Arbeit und Arbeit ist Energiedifferenz (\(W=\Delta E\)). |
Aus dieser vorläufigen Definition folgt, dass Arbeit und Energie in der gleichen Einheit angegeben werden. Die Einheit der Energie ist daher ebenfalls das Joule (\(J\)).
Diese Definition ist keineswegs vollständig. In späteren Kapiteln wirst du zum Beispiel Fälle kennenlernen, in denen verrichtete Arbeit nicht für die spätere Verwendung für mechanische Arbeit zur Verfügung steht und dass es unterschiedliche Qualität von Energie gibt.
5.3.2 Energieformen in der Mechanik
Nach der obigen Definition von Energie kann für jede Form von Arbeit eine entsprechende Energieform angegeben werden. Nach den bisher besprochenen Formen von mechanischer Arbeit ergeben sich die folgenden mechanischen Energieformen:
- Lageenergie (als Folge der Hubarbeit)
- Spannenergie (als Folge der elastischen Verformungsarbeit)
- Bewegungsenergie (als Folge der Beschleunigungsarbeit)
Diese werden wir in den folgenden Abschnitten näher besprechen. Im Buchteil über Rotation wirst du dann noch die Rotationsenergie als weitere mechanische Energieform kennenlernen.
5.3.3 Lageenergie
Hebst du einen Körper auf der Erde, verrichtest du Hubarbeit gegen die Gewichtskraft des Körpers. Am Endpunkt besitzt der Körper Lageenergie (oder potenzielle Energie, engl. gravitational potential energy) in Form von gespeicherter Hubarbeit.
| \[\begin{equation} E_\text{pot}=m\cdot g\cdot h \tag{5.6} \end{equation}\] |
In dieser Formel bedeuten:
- \(E_{\mathrm{POT}}\), die Lageenergie des Körpers (in \(\mathrm{J}\))
- \(m\), die Masse des Körpers (in \(\mathrm{kg}\))
- \(g\), die Fallbeschleunigung (in \(\mathrm{m}/\mathrm{s}^2\))
Diese Formel setzt voraus, dass innerhalb der Hubhöhe die Fallbeschleunigung annähernd unverändert bleibt. Für größere Hubhöhen muss die Formel für die potenzielle Energie im Gravitationsfeld verwendet werden.
5.3.4 Spannenergie
Spannst du beispielsweise die Sehne eines Bogens, verrichtest du elastische Verformungsarbeit. Ein gespannter Bogen besitzt Spannenergie (engl. elastic potential energy) in Form von gespeicherter elastischer Verformungsarbeit.
| \[\begin{equation} E_\text{SPANN}=\frac{k\cdot x^2}{2} \tag{5.7} \end{equation}\] |
In dieser Formel bedeuten:
- \(E_{\mathrm{SPANN}}\), die Verformungsenergie des Körpers (in \(\mathrm{J}\))
- \(k\), die Federkonstante des elastischen Materials (in \(\frac{\text{N}}{\text{m}}\))
- \(x\), die Auslenkung (in \(\mathrm{m}\))
Die Spannenergie ist ebenfalls eine Form von potenzieller Energie. Mit dem Formelsymbol \(E_\text{pot}\) ist aber fast immer die Lageenergie im Gravitationsfeld gemeint.
5.3.5 Bewegungsenergie
Beschleunigst du einen ruhenden Gegenstand auf eine Endgeschwindigkeit \(v\), hast du Beschleunigungsarbeit an dem Körper verrichtet. Der Körper besitzt Bewegungsenergie (oder kinetische Energie, engl. kinetic energy) in Form von gespeicherter Beschleunigungsarbeit.
| \[\begin{equation} E_\text{kin}=\frac{m\cdot v^2}{2} \tag{5.8} \end{equation}\] |
In dieser Formel bedeuten:
- \(E_{\mathrm{KIN}}\), die Bewegungsenergie des Körpers (in \(\mathrm{J}\))
- \(m\), die Masse des Körpers (in \(\mathrm{kg}\))
- \(v\), die Geschwindigkeit des Körpers (in \(\mathrm{m}/\mathrm{s}\))
Wird ein Körper in Drehung versetzt, besitzt er ebenfalls Bewegungsenergie. Diese wird Rotationsenergie genannt und wird später im Buchteil über die Drehbewegung besprochen.
5.3.6 Wo ist der Nullpunkt bei der potenziellen Energie?
Du bist in einem Raum, in dem ein Ball (\(0{,}1\;\mathrm{kg}\)) am Boden liegt. Hebst du ihn um \(1\;\mathrm{m}\) (5.16, links) in die Höhe (Hubhöhe). Gehen wir von einer Fallbeschleunigung von \(g=10\;\mathrm{m/s^2}\) aus, erhältst du eine Hubarbeit von \(W=m\cdot g\cdot h=1\;\mathrm{J}\). Beim Heben hat die potenzielle Energie des Balls daher um \(1\;\mathrm{J}\) zugenommen. Am Endpunkt wirst du dem Ball vermutlich die Energie \(E_\text{pot}=1\;\mathrm{J}\) zuschreiben. Entsprechend wirst du dem Ball vor dem Heben (also, wenn er noch auf dem Boden liegt), die Energie \(E_\text{pot}=0\;\mathrm{J}\) zuordnen.
Stell dir jetzt vor, der Raum befindet sich im 5. Stock eines Hochhauses (5.16, rechts). Der Boden des Raumes befindet sich \(H=10\;\mathrm{m}\) über dem Erdboden. Der Ball muss also irgendwann in der Vergangenheit in den 5. Stock gebracht worden sein. Müsste dann nicht eigentlich der Erdboden als \(E_\text{pot}=0\;\mathrm{J}\) festlegen werden? In diesem Fall hätte der Ball am Zimmerboden bereits die Energie \(E_\text{pot}=10\;\mathrm{J}\) und nach dem Heben im 5. Stock die Energie \(E_\text{pot}=11\;\mathrm{J}\).
Anders als bei der kinetischen Energie (\(v=0\;\mathrm{m/s}\) entspricht \(E_\text{kin}=0\;\mathrm{J}\)) und der Spannenergie (\(x=0\;\mathrm{m}\) entspricht \(E_\text{spann}=0\;\mathrm{J}\)) ist der Nullpunkt bei der potenziellen Energie beliebig wählbar. Physikalisch wichtig ist immer nur die Änderung der potenziellen Energie und diese ist in beiden Fällen nach dem Heben gleich (\(1-0=1\) wie auch \(11-10=1\)). Selbst wenn du den Zimmerboden als \(E_\text{pot}=0\;\mathrm{J}\) gewählt hast und den Ball dann durch das offene Fenster auf die Straße \(E_\text{pot}=-10\;\mathrm{J}\) wirfst, gibt es kein Problem. In diesem Fall wird die Energie \((1-(-10))=11\;\mathrm{J}\) frei, um den Ball zu beschleunigen.
Da du den Nullpunkt für die potenzielle Energie frei wählen kannst, wirst du ihn bei einer konkreten Aufgabe natürlich so wählen, dass die Zahlen möglichst klein sind. Sobald du dich für einen Nullpunkt entschieden hast, musst du alle weiteren potenziellen Energie-Werte relativ zu diesem angegeben.
5.3.7 Energieerhaltungssatz
Betrachten wir ein (reibungsfrei) schwingendes Pendel (Bild 5.17).
Zu Beginn wurde der Pendelkörper irgendwann einmal angehoben (an ihm wurde Hubarbeit verrichtet) und aus der Ruhelage ausgelenkt. Bevor der Pendelkörper losgelassen wurde, ist diese Arbeit als potenzielle Energie im Pendel gespeichert. Nach dem Loslassen beginnt der Pendelkörper sich nach unten zu bewegen. Dabei verringert sich die Höhe und die potenzielle Energie nimmt ab, sie sorgt für die Beschleunigungsarbeit. Wird der Körper immer schneller, nimmt seine kinetische Energie zu. Am tiefsten Punkt ist der Pendelkörper am schnellsten und die ganze potenzielle Energie hat sich in kinetische Energie umgewandelt. Ab diesem Zeitpunkt bewegt sich das Pendel auf der anderen Seite wieder in die Höhe und wird wieder langsamer. Am Umkehrpunkt ist die Geschwindigkeit dann wieder null und damit auch die kinetische Energie – sie hat sich wieder in potenzielle Energie umgewandelt.
Dieses Experiment zeigt, dass sich Energieformen ineinander umwandeln können. Es zeigt aber auch, dass die Gesamtenergie – Summe aller Energieformen – immer gleich bleibt. Energie ist damit eine Bilanzgröße: Was bei einer Energieform wegfällt, kommt bei einer anderen Energieform hinzu. Diese Erfahrung ist im Energieerhaltungssatz (kurz Energiesatz) (engl. conservation of energy) zusammengefasst.
| In einem abgeschlossenen System ist die Gesamtenergie immer konstant. Energie kann sich von einer Form in eine andere Form umwandeln. Energie selbst kann aber weder zerstört noch erzeugt werden. |
Was genau ist mit dem Begriff abgeschlossenes System (engl. isolated system) gemeint? Unter einem physikalischen System kannst du dir einen fix gewählten Ausschnitt aus der Natur vorstellen. In diesem Zusammenhang bedeutet „abgeschlossen“, dass weder Energie über die Systemgrenze nach außen dringt, noch dass Energie von außerhalb des Systems in das System eindringt.
Auf der rechten Seite von Bild 5.18 ist ein abgeschlossenes System mit einem Pendel dargestellt. Auf der linken Seite von Bild 5.18 befindet sich ein nicht-abgeschlossenes System: Die Hand von außerhalb des Systems verrichtet Arbeit an einem Körper innerhalb des Systems.
Links:
- Applet: Skaterpark
5.3.8 Was ist so toll an der Energieerhaltungssatz?
Sprechen Physikerinnen und Physiker über die Energieerhaltung, klingt es so, als würden sie über den heiligen Gral der Physik sprechen. Um zu verstehen, warum sie von der Energieerhaltung so begeistert sind, betrachten wir ein Beispiel.
Ein Achterbahn-Wagen durchfährt eine komplizierte Bahn (Bild 5.19). Wie groß ist seine Geschwindigkeit am Ende der Bahn, wenn er am Anfang der Bahn ruht (\(v=0\;\mathrm{m/s}\))?
Über die Hangabtriebskraft kannst du dir zu jedem Zeitpunkt die Beschleunigung ausrechnen und über die Definitionsgleichungen von Beschleunigung und Geschwindigkeit die Geschwindigkeitsänderung und die Ortsänderung berechnen. Damit lässt sich die Endgeschwindigkeit mühsam Schritt für Schritt berechnen.
Haben wir die Energieerhaltung als Werkzeug zur Verfügung, lässt sich die Aufgabe erstaunlich einfach lösen. Zu Beginn der Fahrt befindet sich der Wagen in Ruhe. Damit ist seine kinetische Energie null. Der Endpunkt der Strecke liegt \(h\) Meter unterhalb des Startpunktes. Daher hat der Wagen am Ende eine potenzielle Energie von \(E_\text{pot}=m\cdot g\cdot h\) verloren, die als Beschleunigungsarbeit an dem Wagen verrichtet wurde. Die verlorene potenzielle Energie ist am Ende der Strecke in der kinetischen Energie des Wagens enthalten.
\[ \begin{array}{rcll} E_\text{kin} & = & E_\text{pot} \\ \frac{\displaystyle m\cdot v^2}{\displaystyle 2} & = & m\cdot g\cdot h &\Bigr\rvert\cdot \frac{\displaystyle 2}{\displaystyle m}\\ v^2 & = & 2\cdot g\cdot h &\Bigr\rvert\cdot \sqrt{\ldots}\\ v & = & \sqrt{2\cdot g\cdot h} \\ \end{array} \]
Und das Genialste daran: Wir konnten die Aufgabe lösen, ohne überhaupt den genauen Verlauf der Strecke zu berücksichtigen! Das Ergebnis ist also unabhängig von dem tatsächlichen Streckenverlauf zwischen Anfangs- und Endpunkt.
Das Konzept von Energie – und vor allem das der Energieerhaltung – ist ein unglaublich mächtiges Werkzeug, um komplizierte Zusammenhänge relativ einfach zu berechnen oder zu verstehen. Es ist kaum übertrieben zu behaupten, dass die Energie der Schlüssel zum Verständnis des Universums ist.
5.3.9 Widerspruch zum Energieerhaltungssatz?
Hebe einen Gummiball in die Höhe und lass ihn fallen. Nach kürzester Zeit bleibt der Ball am Boden liegen. Er hat jetzt keine potenzielle und auch keine kinetische Energie mehr (Bild 5.20). Das widerspricht doch dem Energieerhaltungssatz, oder?
Vor genau solchen Situationen standen Physikerinnen und Physiker in den letzten Jahrhunderten auch immer wieder. Doch jedes Mal, wenn ein Experiment gefunden wurde, das scheinbar der Energieerhaltung widersprach, konnte bisher stets eine neue Energieform gefunden werden, welche die (vermeintlich) fehlende Energie zu erklären vermochte. Es konnte bisher kein einziges Experiment gefunden werden, bei dem der Energieerhaltungssatz nicht gilt. Im Laufe der Zeit sind neben den drei oben genannten mechanischen Energieformen viele weitere entdeckt worden: Schallenergie, innere Energie, elektrische Energie, chemische Energie und noch viele weitere. Du wirst diese und auch noch weitere Energieformen nach und nach in diesem Buch kennenlernen.
In unserem Beispiel mit dem Gummiball ist die ursprüngliche Hubarbeit in innere Energie des Gummiballs übergegangen – seine Temperatur hat sich ein klein wenig erhöht.
Links:
Was ist Energie? Der bekannte Physiker Richard Feynman erklärt in dieser Geschichte das Prinzip der Energieerhaltung mit einem Jungen, der Spielsachen vor seiner Mutter versteckt (englischer Originaltext)
Applet: Skaterpark | Reibung
5.3.10 Perpetuum mobile
Die Bezeichnung Perpetuum mobile kommt aus dem Lateinischen und bedeutet „sich ständig Bewegende“. Unter diesem Begriff ist eine Maschine gemeint, die ohne Energiezufuhr funktioniert und dabei ständig Arbeit verrichtet. So eine Maschine widerspricht aber dem Energieerhaltungssatz. Heute wissen wir daher, dass eine solche Maschine unmöglich ist.
Eine Maschine, die keine Arbeit verrichtet und sich ständig weiterbewegt, widerspricht zwar nicht dem Energiesatz, ist aber aufgrund der immer vorhandenen Reibung praktisch unmöglich, so wie die in Bild 5.21 dargestellte „Maschine“.
In der Wikipedia findest du einige bekannte Beispiele für sogenannte Schein-Perpetuum-mobile. Auch Video-Portale im Internet sind eine wahre Fundgrube für vermeintlich funktionierende perpetuum mobila. Aber lass dich von diesen „Beweisvideos“ nicht täuschen: sie alle verwenden Tricks wie zum Beispiel versteckte Batterien oder beziehen kleine Mengen Energie aus der Umgebung (engl. energy harvesting), um ihre Bewegung trotz Reibung aufrechtzuerhalten.
Ein Beispiel dafür ist die Beverly Clock am physikalischen Institut der University of Otago in Neuseeland. Sie zeigt dort die Zeit seit 1864 an, ohne jemals aufgezogen worden zu sein! Die Energie für den Betrieb stammt ausschließlich aus den täglichen Temperatur- und Luftdruckschwankungen der Umgebung. Die dabei gewonnene Energie wird in einer mechanischen Feder gespeichert und treibt die Uhr an. In dem Modell Atmos (Bild 5.22) genügt schon ein Temperaturunterschied von \(1\;^\circ\mathrm{C}\), um die Uhr für etwa 48 Stunden aufzuziehen.
