4.5 Federkraft
Sicher bist du schon einmal auf einem Trampolin gesprungen (Bild 4.33).
Ein wichtiger Bestandteil jedes Trampolins sind die Schraubenfedern am Rand. In diesem Kapitel geht es um die Kräfte bei elastischen Körpern.
4.5.1 Kraft-Weg-Diagramm einer Schraubenfeder
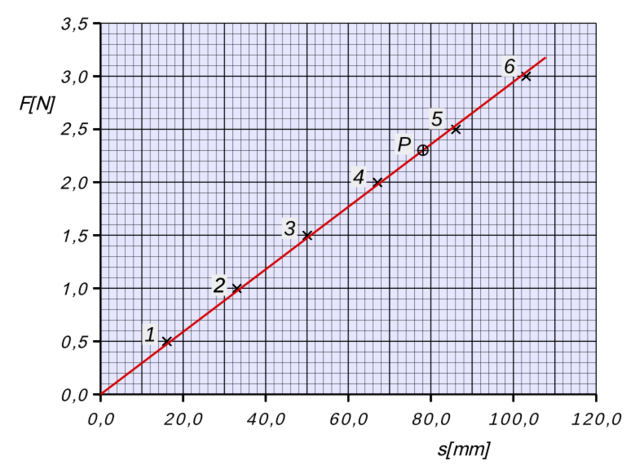
In Bild 4.34 siehst du das Kraft-Weg-Diagramm einer Schraubenfeder. Hier kannst du die Größe Kraft ablesen, die notwendig ist, um eine Schraubenfeder zu dehnen.
Wie du am Diagramm erkennen kannst, bewirkt eine doppelt so große Auslenkung eine doppelt so große Kraft. Es gibt also einen linearen Zusammenhang zwischen Auslenkung und Kraft.
4.5.2 Hookesche Gesetz
Das Verhalten von elastischen Körpern (wie etwa Schraubenfedern oder Gummiringe) wird durch das Hookesches Gesetz (engl. Hooke’s law) beschrieben.
| \[\begin{equation} F_{\mathrm{x}} = -k \cdot x \tag{4.5} \end{equation}\] |
Die Auslenkung aus dem entspannten Zustand (Gleichgewichtslage) wird als Elongation \(x\) bezeichnet. Wird der Körper gedehnt ist die Elongation positiv, wird der Körper gestaucht, ist die Elongation negativ.
Im Diagramm 4.35 ist die Kraft eingezeichnet, die notwendig ist, die Feder zu stauchen oder zu dehnen. Das Hookesches Gesetz beschreibt aber die Rückstellkraft der Feder. Diese ist genau entgegengesetzt der auf die Feder einwirkenden Kraft. Um die Richtung der Federkraft auszudrücken, enthält die Gleichung das Minus. Benötigst du in deinen Berechnungen keine Richtungsinformation, kannst du das Minus einfach weglassen.
Links:
- WebApp: Hookesches Gesetz
4.5.3 Federkonstante
Der Proportionalitätsfaktor \(k\) heißt Federkonstante (engl. spring constant) und gibt die Steifigkeit (Härte) der Feder an. Sie muss für jeden elastischen Körper experimentell bestimmt werden. Sie hängt von Material, Länge und Form des elastischen Körpers ab.
Im Diagramm 4.36 siehst du zwei unterschiedlich starke Schraubenfedern. Um die gleiche Elongation zu erreichen, ist bei der blauen Schraubenfeder eine fast doppelt so große Kraft als bei der roten Schraubenfeder notwendig. Die Federkonstante der blauen Schraubenfeder ist daher größer.
4.5.4 Einheit der Federkonstante
Die Einheit der Federkraft ist – wie die Einheit jeder Kraft – Newton. Die Elongation ist eine Länge und wird in der Einheit Meter angegeben. Für die Herleitung der Einheit der Federkonstante formen wir das Hookesche Gesetz um (Vorzeichen spielen bei der Dimensionsbetrachtung keine Rolle):
\[ [k] = 1\;\frac{[F_{\mathrm{x}}]}{[x]} = 1\;\frac{\text{N}}{\text{m}} \]
Die Einheit der Federkonstante ist also “Newton pro Meter”. Die Federkonstante gibt an, welche Kraft notwendig ist, um die entsprechende Schraubenfeder um \(1\;\text{m}\) zu dehnen (oder zu stauchen). In der Praxis wird die Federkonstante von Schraubenfedern oft in der Einheit \(\text{N}/\text{cm}\) (Newton pro Zentimeter) angegeben.
4.5.5 Elastizitätsbereich
Elastische Körper können durch Kräfte verformt werden. Hört die Kraft auf zu wirken, nimmt der Körper seine ursprüngliche Form wieder ein. Diese Art der Verformung wird reversibel genannt.
Jeder elastische Körper ist aber nur bis zu einer gewissen Grenze elastisch. Ist die Kraft zu groß, findet auch bei einem elastischen Körper eine dauerhafte Verformung statt, oder er wird sogar zerstört. Diese Grenze wird Elastizitätsgrenze (engl. elasticity limit) genannt. Für alle Kräfte unterhalb dieser Grenze befindet sich der Körper im Elastizitätsbereich (Proportionalitätsbereich) (engl. elasticity range). Nur in diesem Bereich ist das Hookesche Gesetz gültig (Bild 4.37).
Neben elastischen Körpern gibt es auch plastische Körper (wie etwa Knetmasse oder weicher Metalldraht). Sie werden durch jede Krafteinwirkung dauerhaft verformt. Ihre Verformung ist immer irreversibel.
4.5.6 Federkraftmesser
Das Hookesche Gesetz ist die Grundlage für einen Federkraftmesser (engl. force meter). Weil die Federkraft zur Dehnung proportional ist, ist die Skala eines Federkraftmessers immer linear (Bild 4.38).