4.4 Gewicht
Im Bild 4.22 siehst du, wie der bekannte Physiker Stephen Hawking die Schwerelosigkeit erlebt.

Bild 4.22: Der Physiker Stephen Hawking in Schwerelosigkeit
In diesem Kapitel geht es um die Gewichtskraft, den Unterschied zwischen Gewicht und Masse und den faszinierenden Zustand der Schwerelosigkeit.
4.4.1 Gewichtskraft
Hängst du dasselbe Massestück auf der Oberfläche verschiedener Himmelskörper an eine Federwaage, misst du die lokale Gewichtskraft (kurz Gewicht) (engl. weight) dieses Körpers (Bild 4.23).
Die Gewichtskraft ist die Folge der Gravitationskraft zwischen Himmelskörper und Gegenstand und Fallbeschleunigung an dem jeweiligen Ort (Ortsfaktor) berechnet werden. Setzt du in der Formel für das dynamische Grundgesetz für die Beschleunigung den Ortsfaktor ein, erhältst du:
| \[\begin{equation} \vec{F} = m\cdot \vec{g} \tag{4.4} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(\vec{F}\) Gewichtskraft des Körpers an diesem Ort (in \(\mathrm{N}\))
- \(m\) Masse des Körpers (in \(\mathrm{kg}\))
- \(g\) Fallbeschleunigung an diesem Ort (in \(\mathrm{m/s^2}\))
4.4.2 Gewichtskraft auf der Erde
Besitzt du eine Masse von, sagen wir \(60\;\mathrm{kg}\), hast du in Mitteleuropa (\(g=9{,}81\;\mathrm{m}/\mathrm{s}^2\)) ein Gewicht (eine Gewichtskraft) von ungefähr \(600\;\mathrm{N}\).
Die Masse eines Körpers im gesamten Universum unverändert gleich. Ändert sich von Ort zu Ort die Fallbeschleunigung, ändert sich mit ihr die Gewichtskraft des Körpers (Bild 4.24).
4.4.3 Masse und Gewicht
Wirst du nach deinem Gewicht gefragt, antwortest du vermutlich mit „so-und-so-viel Kilogramm“. Das Kilogramm ist aber die SI-Einheit der Größe Masse. Sind also die Begriffe Masse und Gewicht gleich? Die Antwort ist: Nein! Bei Gewicht handelt es sich um eine Kraft und die Einheit ist Newton.
In Bild 4.25 siehst du dasselbe Gewicht auf Erde, Mond und Mars – also unterschiedliche Massen, die auf den Oberflächen der Himmelskörper dieselbe Gewichtskraft aufweisen.
Während das Gewicht eines Körpers null sein kann (wenn zum Beispiel keine Schwerkraft auf ihn wirkt), kann die Masse eines Körpers niemals null sein.
4.4.4 Wiegen mit einer Balkenwaage
Wenn Masse und Gewicht unterschiedliche Größen sind, warum werden dann beide Begriffe in der Alltagssprache synonym verwendet? Vermutlich liegt es daran, dass in früheren Zeiten Handelswaren mit einer Balkenwaage (Bild 4.26) abgewogen wurden.
Das Abwiegen mit einer Balkenwaage entspricht einem Massenvergleich am selben Ort. Am selben Ort haben gleiche Massen auch die gleiche Gewichtskraft (da der Ortsfaktor gleich ist). Bei einer Balkenwaage bekommst du also für \(1\;\mathrm{kg}\) immer dieselbe Menge Äpfel – egal ob auf der Erde, auf dem Mond oder auch auf dem Mars (Bild 4.27). In diesem Fall spielt es keine Rolle, ob du von Gewicht(kraft) oder Masse sprichst.
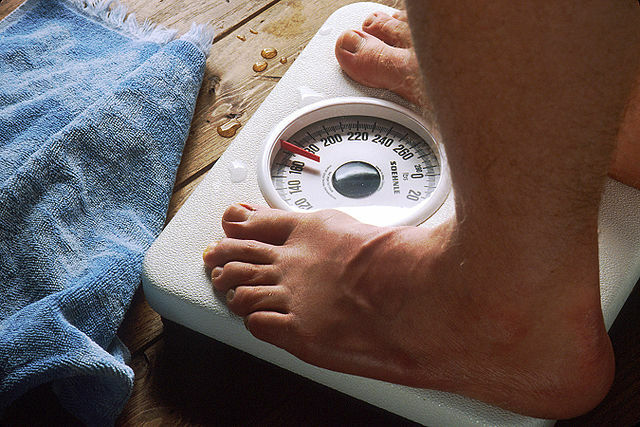
4.4.5 Wiegen mit einer Personenwaage
Moderne Waagen, wie etwa eine Personenwaage (Bild 4.28), vergleichen keine Massen, sondern messen die Gewichtskraft. Im Gegensatz zu einer Federwaage „rechnen“ sie die Gewichtskraft mit einem fix gespeicherten Ortsfaktor in Masse um und zeigen das Ergebnis in Kilogramm an.
Diese Waagen sind auf einen bestimmten Ort geeicht und zeigen das falsche Ergebnis an, sobald sie zur Messung an einem Ort mit einem anderen Ortsfaktor verwendet werden! Nimmst du also eine Personenwaage von deinem Badezimmer mit auf den Mars, ohne sie vor Ort neu zu eichen, zeigt die Waage bei gleicher Masse weniger Kilogramm an als auf der Erde. Für eine bloße Gewichtsreduktion reicht es daher, auf einen Himmelskörper mit kleinerem Ortsfaktor zu reisen. Die Weight Watchers sollten daher eigentlich Mass Watchers heißen und ihre Mitglieder sollten keine Gewichtsreduktion, sondern vielmehr eine Massenreduktion anstreben.
4.4.6 Bestimmung der Lage bei Mobilgeräten
Um die Lage im Raum zu bestimmen, misst ein Smartphone oder Tablet die Beschleunigung mit Sensoren. Der mechanische Teil des Sensors funktioniert ähnlich wie der eines Federkraftmessers. Statt der Schraubenfeder verwendet der Sensor wenige Mikrometer breite Siliziumstäbe. Kommt es zu einer Formänderung der Stäbe, ändern sich die elektrischen Eigenschaften im Bauteil. Ein Smartphone besitzt drei dieser Sensoren, die paarweise orthogonal angeordnet sind. Aus der Änderung aller drei Sensoren kann die Elektronik berechnen, wo bei dem Gerät gerade „unten“ ist und den Bildschirminhalt entsprechend drehen.
Glücklicherweise halten sich alle Hersteller von Smartphones an folgendes Koordinatensystem . Hältst du dein Smartphone aufrecht, dass du am Hauptdisplay lesen kannst ist (Bild 4.29), dann zeigt
- nach rechts die positive x-Achse
- nach links, die negative x-Achse
- nach oben, die positive y-Achse
- nach unten, die negative y-Achse
- zu dir, die positive z-Achse
- von dir weg, die negative z-Achse
Alle Sensor-Werte, die du von deinem Smartphone ausliest, sind relativ zu diesem Koordinatensystem angegeben.
- Video: Aufbau und Funktionsweise des Sensors.
- Smartphone App: Auslesen des Beschleunigungssensors auf deinem Smartphone
4.4.7 Schwerelosigkeit
Bist du im Zustand der Schwerelosigkeit, spürst du keine Wirkung der Gewichtskraft. Das kann mehrere Ursachen haben.
Würdest du dich in einem leeren Universum befinden (keine Sterne, keine Planeten,…) wärst du schwerelos, weil es gar keine Gewichtskraft gibt, die wirken kann.
Eine andere Möglichkeit bestünde, wenn du dich zwischen zwei Himmelskörpern (zum Beispiel der Erde und dem Mond) befindest und sich die Anziehungskräfte gerade aufheben (Abarischer Punkt). Dieser Punkt wird zum Beispiel bei Mondmissionen durchflogen.
Beim Schwimmen oder Tauchen erlebst du Schwerelosigkeit, weil Gewichts- und Auftriebskraft einander aufheben.
Kurzfristig bist du auch schwerelos, wenn du von einem Podest herunterspringst. Im Gegensatz zu den letzten Beispielen gibt es hier eine Gewichtskraft, aber aufgrund des freien Falls kannst du ihre Wirkung nicht spüren.
Um die Zeit im freien Fall (also in Schwerelosigkeit) zu verlängern, kannst du ein Trampolin verwenden (Senkrechter oder lotrechter Wurf). Mit diesem Trick verdoppeln die Physikerinnen und Physiker am Bremer Fallturm die Zeit für ihre Experimente in Schwerelosigkeit auf \(9\;\mathrm{s}\).
Auch jeder Körper beim schrägen Wurf befindet sich im freien Fall. Fliegt ein Flugzeug genau entlang einer Wurfparabel, sind die Insassen für die Dauer des Parabelfluges ebenfalls schwerelos (Bild 4.30). Damit lässt sich ein schwereloser Zustand von bis zu \(25\;\mathrm{s}\) erreichen.
- Die Mannschaft an Bord der Internationalen Raumstation (ISS) ist dagegen ständig in Schwerelosigkeit (Bild 4.31).
Der Grund ist der Gleiche wie in den vorherigen Beispielen: Die ISS ist ständig im freien Fall. Warum sie nicht zu Boden fällt, liegt an ihrer großen horizontalen Geschwindigkeit von rund \(28.000\;\mathrm{km/h}\). Mit dieser Bahngeschwindigkeit fällt sie in einer kreisförmigen Bahn um die Erde herum und bleibt immer in derselben Entfernung zur Erdoberfläche (Bild 4.32).
Die im englischen Sprachraum manchmal verwendete Bezeichnung zero gravity für diese Art der Schwerelosigkeit ist allerdings falsch! Die ISS befindet sich bei ihrer Umlaufbahn in einer Höhe von nur ca. \(400\;\mathrm{km}\) über dem Erdboden. In dieser Höhe beträgt die Fallbeschleunigung immer noch \(g=8{,}73\;\mathrm{m}/\mathrm{s}^2\) – das sind nur rund \(10\,\%\) weniger als auf der Erdoberfläche! Auf die Astronauten an Bord der ISS wirkt also sehr wohl die Schwerkraft. Die Astronauten haben eine fast gleich große Gewichtskraft wie auf der Erde, aber aufgrund des freien Falls können sie diese Kraft nicht spüren.
Links:
- Video: Parabelflug mit einem Airbus 310, wie er von der europäischen Weltraumorganisation ESA verwendet wird
- Video: Der bekannte Physiker Stephen Hawking († 2018), der an einer motorischen Erkrankung litt, erlebt die Schwerelosigkeit bei einem Parabelflug