15.4 Statischer Auftrieb
Die meisten Menschen lieben es, Zeit im Wasser zu verbringen (Bild 15.25). Ein Grund dafür ist, dass wir uns darin fast schwerelos fühlen. Auch schwere Objekte lassen sich leichter heben. Das Wasser scheint die Schwerkraft (teilweise) aufzuheben.
In diesem Kapitel geht es um das Phänomen des Auftriebs und die damit verbundene Auftriebskraft.
15.4.1 Archimedisches Prinzip
Stell dir ein Gefäß mit ruhendem Wasser vor. Wir trennen gedanklich ein Wasservolumen von der restlichen Flüssigkeit ab (praktisch auch durch eine hauchdünne Kunststoff-Folie durchführbar). Was ändert sich dadurch? Gar nichts. Alle Teile der Flüssigkeit sind weiterhin unbewegt. Daher müssen sich für das abgegrenzte Wasservolumen die nach unten gerichtete Gewichtskraft und die nach oben gerichtete Auftriebskraft die Waage halten (Bild 15.26, links).

Bild 15.26: Auftriebskraft und Gewichtskraft eine gedachten Wasservolumens und eines durch ihn ersetzten Körpers
Ersetzen wir das abgegrenzte Wasservolumen durch einen Körper aus einem anderen Material, ändert das nichts an der umgebenden Flüssigkeit – ihr Druck hängt ausschließlich von der Tiefe ab. Damit ist für jeden Körper mit demselben Volumen die Auftriebskraft gleich groß (Bild 15.26, rechts)! Daraus schließen wir:
| Der Betrag der Auftriebskraft ist gleich groß dem Betrag der Gewichtskraft des verdrängten Fluids. |
Diese Erkenntnis heißt Archimedisches Prinzip (engl. archimedes’ principle). Es ist nach Archimedes von Syrakus benannt, der das Prinzip erkannt haben soll, als er den Betrug mit der vermeintlichen Goldkrone aufdeckte.
Links:
- WebApp: Archimedisches Prinzip
15.4.2 Auftriebskraft
Wenn du ins Wasser gehst, ändert sich die Masse deines Körpers nicht und somit muss auch deine Gewichtskraft unverändert bleiben. Im Wasser fühlst du dich aber „leichter“. Daher muss die Flüssigkeit eine – nach oben gerichtete – zusätzliche Kraft erzeugen. Diese der Schwerkraft entgegengesetzte Kraft wird Auftriebskraft (kurz: Auftrieb) (engl. buoyancy) genannt.
Die Auftriebskraft ist eine Folge des hydrostatischen Drucks. Nach dem Archimedischen Prinzip entspricht der Betrag der Auftriebskraft der Gewichtskraft des verdrängten Flüssigkeitsvolumens.
| \[\begin{equation} F_A = \rho_{Fl}\cdot g\cdot V \tag{15.5} \end{equation}\] |
In dieser Formel bedeuten:
- \(F_A\), die Auftriebskraft in einer Flüssigkeit (in \(\mathrm{N}\))
- \(\rho_{Fl}\), die Dichte der Flüssigkeit (in \(\mathrm{kg/m^3}\))
- \(g\), die Fallbeschleunigung (in \(\mathrm{m/s^2}\))
- \(V\), das von dem Körper verdrängte Flüssigkeitsvolumen (in \(\mathrm{m}^3\))
Die um die Auftriebskraft verminderte Gewichtskraft eines Körpers wird manchmal als scheinbares Gewicht oder vermindertes Gewicht bezeichnet (engl. apparent weight).
Links:
15.4.3 Herleitung der Auftriebskraft
Um zu verstehen, warum der hydrostatische Druck die Ursache für den Auftrieb ist, sieh dir das Bild 15.27 eines vollständig in eine Flüssigkeit getauchten Quaders an.
Stell dir die Oberfläche des Quaders in kleine, gleich große Flächen unterteilt vor. Auf jeder dieser Flächen ist die Druckkraft eingezeichnet. Auf der Oberseite des Quaders sind alle Kräfte gleich groß – sie befinden sich alle in der gleichen Tiefe \(h_1\). Somit herrscht überall der gleiche hydrostatische Druck. Auf der Unterseite wirkt ebenfalls auf jedes Flächenelement die gleiche Kraft. Allerdings sind diese Kräfte größer als an der Oberseite, da in der Tiefe \(h_2\) ein größerer hydrostatischer Druck herrscht.
Auf die Seitenflächen wirkt keine einheitliche Druckkraft auf die Flächenelemente. Je tiefer, desto größer die Kraft. Auf jeder Höhe gibt es aber eine gleich große entgegengesetzte Kraft von der gegenüberliegenden Seite, sodass sich die Kräfte auf die Seitenflächen alle ausgleichen.
Die Auftriebskraft ist die Differenz der Kräfte aufgrund- und Deckfläche des Körpers.
\[ \begin{array}{rcl} F_A & = & F_2-F_1\\ & = & p_2\cdot A - p_1\cdot A \\ & = & \rho_{Fl}\cdot g\cdot h_2\cdot A - \rho_{Fl}\cdot g\cdot h_1\cdot A \\ & = & \rho_{Fl}\cdot g\cdot A \cdot( h_2-h_1) \\ & = & \rho_{Fl}\cdot g\cdot V \\ \end{array} \]
Die Höhendifferenz \(h = h_2-h_1\) entspricht genau der Höhe des Quaders. Das Produkt von Grundfläche \(A\) und Höhe \(h\) ergibt das Volumen des Quaders.
Wir haben die Formel für die Auftriebskraft einfachheitshalber für einen Quader hergeleitet. Das Ergebnis ist aber unabhängig von der Form des Körpers und gilt für vollständig oder auch nur teilweise in ein Fluid eingetauchte Körper.
15.4.4 Auftrieb als Energieminimum
Von allein strebt jedes System den Zustand kleinster potenzieller Energie (engl. principle of minimum potential energy (PMPE)) an. Dieses Prinzip der minimalen Energie lässt sich auch beim Auftrieb beobachten.
Die Parabel in Bild 15.28 zeigt den Wert der Summe der potenziellen Energien von Körper und Flüssigkeit in Abhängigkeit von der Eintauchtiefe des Körpers. In der Mitte siehst du die Eintauchtiefe, die der Körper nach dem Archimedischen Prinzip einnimmt. In diesem Zustand ist der gemeinsame Schwerpunkt aus Körper und Wasser am kleinsten. Jede andere Eintauchtiefe führt zu einem Anheben des Gesamtschwerpunkts.
Vielleicht wunderst du dich, dass die Gesamtenergie durch eine Parabel beschrieben wird, obwohl sich doch die potenzielle Energie eines Körpers linear mit der Höhe ändert. Für den eingetauchten (starren) Körper gilt das, aber beim Wasservolumen ist das anders. Ändert sich die Eintauchtiefe des Körpers, verformt sich das Wasservolumen. Die Höhe des Flüssigkeitsschwerpunkts und damit auch die potenzielle Energie des Wassers ist dadurch nicht mehr linear abhängig von der Eintauchtiefe. Für die Summe der beiden Energien (Gesamtenergie) erhalten wir eine quadratische Abhängigkeit von der Eintauchtiefe \(h\), wie sie im Bild zu sehen ist.
Links:
15.4.5 Archimedes und die Krone
Archimedes wurde der Geschichte nach von König Hieron II. von Syrakus beauftragt, herauszufinden, ob seine Krone tatsächlich aus reinem Gold gefertigt wurde oder teilweise aus einem billigeren Metall besteht. Die Krone durfte dabei weder beschädigt noch verändert werden.
In Bild 15.29 siehst du eine Methode, die Reinheit des Kronenmaterials zu überprüfen. Zunächst wird ein Körper aus reinem Gold mit der gleichen Masse wie die Krone hergestellt. Die Gleichheit der Massen wird mit einer Balkenwaage überprüft (links). Sobald die Waagschalen vollständig in Wasser eingetaucht werden, zeigt sich zusätzlich, ob beide Körper auch dieselbe (mittlere) Dichte haben. In unserem Fall war die Krone zum Teil aus einem Material mit geringer Dichte gefertigt. Bei gleicher Masse ist das Volumen der Krone somit größer und verdrängt mehr Wasser. Nach dem archimedischen Prinzip erfährt ein solcher Körper einen größeren Auftrieb, und der Betrug wird offensichtlich (rechts).
Angeblich entdeckte Archimedes sein Prinzip, während er in einer Badewanne saß. Bei der Erkenntnis soll er Heureka! („Ich habe [es] gefunden“) ausgerufen haben. Der Unterschied im Volumen von Krone und der Vergleichsmasse lässt sich prinzipiell auch ganz ohne Auftrieb zeigen. Um zu testen, ob beide Körper dasselbe Volumen besitzen, kann der Wasserpegel beim Eintauchen in eine Flüssigkeit verglichen werden. Die Auftriebsmethode ist aber wesentlich genauer.
Links:
15.4.6 Schwimmen, schweben, sinken
Von der Dichte eines Körpers hängt es ab, wie sich dieser in einer Flüssigkeit verhält.

Bild 15.30: sinken (dunkelgrau), schweben (grau), aufsteigen und schwimmen (hellgrau) in einer Flüssigkeit
sinken: Hat der Körper eine höhere Dichte als die Flüssigkeit (etwa Eisen in Wasser) ist die Gewichtskraft des Körpers größer als die Auftriebskraft und der Körper sinkt auf den Boden (Bild 15.30 links).
schweben: Hat der Körper eine gleich große Dichte wie die Flüssigkeit selbst, schwebt der Körper in jeder Tiefe – weder sinkt noch steigt er (Bild 15.30 Mitte).
schwimmen: Hat der Körper eine kleinere Dichte als die Flüssigkeit (etwa Styropor in Wasser) ist die Gewichtskraft des Körpers kleiner als die Auftriebskraft und der Körper steigt in der Flüssigkeit auf (Bild 15.30 rechts), bis er an der Oberfläche schwimmt. Dabei taucht der Körper gerade so weit in die Flüssigkeit ein, bis die Gewichtskraft der verdrängten Flüssigkeit der Gewichtskraft des Körpers entspricht.
Analog gilt das Archimedische Prinzip für Gase. Weil Helium eine geringere Dichte als Luft hat, steigt ein heliumgefüllter Ballon in der Erdatmosphäre auf. Im Gegensatz zu einer Flüssigkeit nimmt die Dichte der Luft mit der Höhe ab. Ein Ballon steigt daher nur bis zu einer Maximalhöhe auf, in der die Dichte der Luft so weit abgenommen hat, dass sich Auftriebskraft und Gewichtskraft die Waage halten.
Bisher sind wir von homogenen Körpern ausgegangen, also von Körpern einheitlicher Dichte. Stahlschiffe besitzen Hohlräume und reduzieren so ihre Masse bei gleicher Wasserverdrängung. So können sie schwimmen, obwohl die Dichte von Stahl um ein Vielfaches größer als die von Wasser ist. Bei inhomogenen Körpern wird das Verhältnis von Masse und Volumen als mittlere Dichte (engl. mean density) bezeichnet.
Eine andere Möglichkeit, die Dichte zu verringern, besteht durch Erwärmung. Ein Heißluftballon ist mit derselben Luft gefüllt wie die Umgebung. Allerdings wird die Luft im Ballon erwärmt, dehnt sich aus und steigt in der kühleren Umgebungsluft auf (15.31). Der Temperaturunterschied führt auch in Flüssigkeiten zu einem Auftrieb, wie im Fall der Konvektion.
Links:
- Video: Schwimmen eines Aluminium-Schiffes auf dem schweren (dichten) Gas Schwefelhexafluorid.
- Applet: Float or Sink Simulator
15.4.7 Schwerelos im Wasser
Da der menschliche Körper zu einem Großteil aus Wasser besteht, ist die Auftriebskraft für eine Person nahezu gleich groß wie ihre Gewichtskraft – wir sind in Wasser fast schwerelos. Die meisten Menschen schwimmen bei angehaltener Luft mit vollen Lungen an der Oberfläche und sinken zu Boden, wenn sie die Luft aus den Lungen entweichen lassen.
Ein großer Wassertank ist also eine sehr einfache und kostengünstige Methode, um Schwerelosigkeit für einen längeren Zeitraum auf der Erde zu simulieren (Bild 15.32).
Ein Neoprenanzug enthält mikroskopisch kleine Lufteinschlüsse. Gase sind schlechte Wärmeleiter und daher schützt dich ein solcher Anzug vor Unterkühlung im Wasser. Gleichzeitig verringert die eingeschlossene Luft aber auch deine mittlere Dichte und erhöht damit die Auftriebskraft. In einem Neoprenanzug schwimmst du auf der Wasseroberfläche wie ein Korken. Taucher tragen eine Tarierweste mit Taschen für Bleigewichte, um ihre Gewichtskraft zu erhöhen. Durch Einblasen oder Ablassen von Luft in die Kammern der Weste kann der Taucher seinen Auftrieb sehr präzise steuern.
Im Meerwasser ist der Salzgehalt höher und damit die Dichte der Flüssigkeit und die Auftriebskraft größer. Im Toten Meer ist der Salzgehalt so groß, dass du auch ohne Neoprenanzug nicht untergehst (Bild 15.25).
15.4.8 Statisches Tauchen
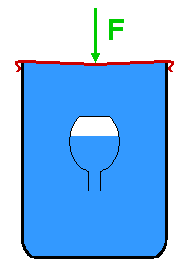
In Bild 15.33 siehst du einen sogenannten Cartesianischen Taucher (engl. Cartesian diver). Bei diesem einfachen – nach René Descartes benannten – Experiment kannst du den Zusammenhang von Auftriebskraft und verdrängtem Flüssigkeitsvolumen direkt beobachten.
Ein unten offenes Gefäß – der Taucher – wird so in eine vollständig mit Flüssigkeit gefüllten Kunststoff-Flasche gegeben, dass sich im Inneren des Tauchers eine Luftblase befindet und der Taucher aufschwimmt. Jetzt wird die Flasche gasdicht verschlossen. Das verdrängte Flüssigkeitsvolumen besteht aus dem Taucher und der Luftblase. Durch das Zusammendrücken der Flasche wird der Wasserdruck erhöht. Das lässt die eingeschlossene Luftblase schrumpfen – ihr Volumen wird kleiner. Dadurch wird weniger Wasser verdrängt und der Auftrieb verringert sich, während das Gewicht des Tauchers unverändert bleibt. Wird die Auftriebskraft kleiner als die Gewichtskraft, sinkt der Taucher in der Flasche zu Boden. Durch Verringern des Drucks auf die Flasche dehnt sich die Luftblase aus und der Taucher steigt wieder. Bist du geschickt, kannst du mit dem richtigen Druck auf die Flasche den Taucher in beliebiger Höhe schweben lassen.
Praktische Anwendung findet dieses Prinzip bei der Schwimmblase von Fischen und dem statischen Tauchen von Tauch- und U-Booten (Bild 15.34).
Damit ein U-Boot abtauchen kann, muss sein Auftrieb verringert werden. Dazu werden Hohlräume im Schiffsrumpf (Ballasttanks) mit Wasser geflutet. Zum Auftauchen muss der Auftrieb wieder erhöht werden. Dazu wird mit Pressluft aus Drucklufttanks das Wasser in den Ballasttanks wieder herausgedrängt.
Links:
15.4.9 Auftriebsschwerpunkt
Wir wissen bereits, dass der Angriffspunkt der Gewichtskraft der Massenmittelpunkt (Gewichtsschwerpunkt) des Körpers ist. Wo ist aber der Angriffspunkt der Auftriebskraft?
Der Angriffspunkt der Auftriebskraft ist der Massenmittelpunkt des verdrängten Fluids. Er wird Auftriebsschwerpunkt (engl. center of buoyancy) genannt. In Bild 15.35 siehst du den Unterschied von Gewichtsschwerpunkt (\(G\)) und Auftriebsschwerpunkt (\(A\)).
Bei einem homogenen, vollständig eingetauchten Körper fallen diese beiden Punkte zusammen. Bei einem Körper, der an der Wasseroberfläche schwimmt, unterscheiden sich diese beiden Punkte fast immer.
15.4.10 Stabiles Schwimmen
Sieh dir das Bild 15.36 an. Befindet sich das Schiff in Schräglage (Bilder oben), bewirken die Auftriebskraft \(F_\text{A}\) und die Gewichtskraft \(F_\text{G}\) ein Drehmoment. In den Bildern darunter siehst du die Wirkung dieses Drehmoments: Während das linke Schiff wieder aufgerichtet wird, kippt das rechte Schiff um (es kentert).
Was ist der Unterschied bei beiden Schiffen? Die relative Lage von Gewichts- und Auftriebsschwerpunkt ist entscheidend. Willst du, dass dein Schiff stets aufrecht schwimmt, musst du bei der Konstruktion (und auch bei der Beladung!) darauf achten, dass sich der Gewichtsschwerpunkt immer unterhalb des Auftriebsschwerpunkts befindet. Nur dann richtet das entstehende Drehmoment dein Schiff von allein immer wieder auf (stabiles Schwimmen).
Früher waren diese physikalischen Gesetzmäßigkeiten noch unbekannt, und Schiffe wurden hauptsächlich nach Erfahrung und Gefühl gebaut. Das wurde dem schwedischen Kriegsschiff Vasa zum Verhängnis. Durch die 64 Kanonen am Deck des Schiffes war der Gewichtsschwerpunkt so hoch, dass es beim Stapellauf 1628 kenterte und sank. Auch wenn ein Schiff stabil schwimmt, kann sich durch Überladung (zum Beispiel beim Sewol Unglück) oder Verrutschen der Fracht (zum Beispiel beim Belpamela Unglück) der Gewichtsschwerpunkt so ungünstig verändern, dass es zum Kentern des Schiffes kommt.
15.4.11 Anwendungsbeispiel: Eisberge
Die Dichte von (Süß-)Wasser beträgt \(1000\;\mathrm{kg/m^3}\). Die Salzwasserdichte der Ozeane hat eine durchschnittliche Dichte von \(\rho_\text{Salzwasser} = 1025\;\mathrm{kg/m^3}\) (das entspricht einem Salzgehalt von rund \(2.1\%\)). Ein Eisberg besteht aus gefrorenem Süßwasser und hat eine Dichte von \(\rho_\text{Eis} = 920\;\mathrm{kg/m^3}\). Berechne den Anteil des Eisbergs, der sich unter Wasser befindet.
Da der Eisberg im Meerwasser schwimmt (weder steigt noch sinkt) ist die Auftriebskraft gleich groß der Gewichtskraft des gesamten Eisbergs.
\[ F_\text{A} = F_\text{G, Eisberg} \]
Die Gewichtskraft \(F_\text{G, Eisberg}\) des gesamten Eisbergs lautet:
\[ \begin{aligned} F_\text{G, Eisberg} = {} & m_\text{Eisberg}\cdot g \\ = {} & \rho_\text{Eis}\cdot V_\text{Eisberg}\cdot g \\ \end{aligned} \]
Nach dem Archimedischen Prinzip entspricht der Auftrieb \(F_\text{A}\) der Gewichtskraft der verdrängten Flüssigkeit. Das Volumen der verdrängten Flüssigkeit ist bei einem schwimmenden Körper das eingetauchte Volumen (Volumen des Körpers unter Wasser) \(V_\text{unten}\):
\[ \begin{aligned} F_\text{A} = {} & \rho_\text{Salzwasser}\cdot V_\text{unten}\cdot g \\ \end{aligned} \]
Setzen wir beide Kräfte gleich, erhalten wir:
\[ \begin{aligned} \rho_\text{Salzwasser}\cdot V_\text{unten}\cdot g = {} & \rho_\text{Eis}\cdot V_\text{Eisberg}\cdot g &&\qquad\Bigr\rvert\cdot \frac{1}{g}\\ \rho_\text{Salzwasser}\cdot V_\text{unten} = {} & \rho_\text{Eis}\cdot V_\text{Eisberg} &&\qquad\Bigr\rvert\cdot \frac{1}{V_\text{Eisberg}\cdot \rho_\text{Salzwasser}}\\ \frac{V_\text{unten}}{V_\text{Eisberg}} = {} & \frac{\rho_\text{Eis}}{\rho_\text{Salzwasser}} \\ \end{aligned} \]
Wir können den Anteil des eingetauchten Eisbergvolumens also direkt aus dem Verhältnis der beiden Dichten berechnen.
\[ \frac{V_\text{unten}}{V_\text{Eisberg}} = \frac{920}{1025} = 0{,}89\ldots = 89{,}75\ldots\% \]
Rund \(90\%\) eines Eisbergs befinden sich unter Wasser! Nur etwa \(\frac{1}{10}\) des Eisbergs ragt sichtbar aus dem Wasser (Bild 15.37) – daher kommt auch die Redewendung „Spitze des Eisbergs“. Entsprechend gefährlich waren Eisberge für die Schifffahrt vor der Verwendung von Radar und Sonar. Das bekannteste Schiffsunglück mit einem Eisberg ist zweifellos der Untergang der Titanic.
Warum bestehen Eisberge immer aus Süßwasser? Salzmoleküle sind in Wasser nur gelöst – die Wasser- und Salzmoleküle gehen keine chemische Bindung ein. Ist die Temperatur tief genug, verbinden sich die Wassermoleküle zu Eiskristallen. Die Salzmoleküle werden dabei einfach links liegengelassen und verbleiben in der flüssigen Phase des Wassers.