15.3 Schweredruck in ruhenden Fluiden
Im Bild 15.11 siehst du einen Taucher mit einer Pressluftflasche bei einem Tauchgang.
Der Lungenautomat versorgt den Taucher in jeder Tiefe mit exakt demselben Luftdruck wie der umgebende Wasserdruck. Nur so kann der Taucher unter Wasser atmen. Wie und warum sich der Wasserdruck mit der Tiefe ändert, erfährst du in diesem Kapitel.
15.3.1 Hydrostatische Druck
Tauchst du in einem Schwimmbad oder in einem See nach unten, spürst du an deinem Trommelfell wie der Druck mit der Tiefe zunimmt. Der Grund dafür ist die Gewichtskraft der Wassermenge, die sich über dir befindet. Diesen Druck wird hydrostatischen Druck (engl. hydrostatic pressure) genannt. Die Formel lautet:
| \[\begin{equation} p = \rho_{Fl}\cdot g\cdot h + p_0 \tag{15.4} \end{equation}\] |
In dieser Formel bedeuten:
- \(\rho_{Fl}\), die Dichte der Flüssigkeit (in \(\mathrm{kg/m^3}\))
- \(g\), die örtliche Fallbeschleunigung (in \(\mathrm{m/s^2}\)),
- \(h\) für die Eintauchtiefe (in \(\mathrm{m}\))
- \(p_0\) für einen zusätzlichen Druck (in \(\mathrm{Pa}\)), der auf die Flüssigkeitsoberfläche wirkt
Betrachten wir konkret den hydrostatischen Druck von Wasser. Bei einer Dichte von \(1000\;\mathrm{kg}/\mathrm{m}^3\) und einer Fallbeschleunigung von rund \(10\;\mathrm{m}/\mathrm{s}^2\) ergibt sich in einer Tiefe von \(10\;\textrm{m}\) ein Druck von:
\[ p = 1000\cdot 10\cdot 10 = 100.000 \;\textrm{Pa} = 1\;\textrm{bar} \]
Dazu kommt noch der Luftdruck auf Meeresniveau \(p_0\) von \(1\;\textrm{bar}\), der über dem Wasser liegt. Der Gesamtdruck ist daher \(2\;\textrm{bar}\). Das Bild 15.12 fasst den Tiefendruck in Wasser noch einmal zusammen.
15.3.2 Herleitung des hydrostatischen Drucks
Die Ursache für den hydrostatischen Druck in einer Tiefe ist die Gewichtskraft der Wassersäule darüber. Für die Herleitung betrachten wir die in Bild 15.13 gezeigte Situation.
In einer Tiefe \(h\) befindet sich eine Fläche \(A\). Die Druckkraft auf diese Fläche wird von dem Wasservolumen \(A\cdot h\) (Grundfläche mal Höhe) erzeugt.
\[ \begin{array}{rcl} p & = & \displaystyle\frac{F_G}{A} \\ & = & \displaystyle\frac{m\cdot g}{A} \\ & = & \displaystyle\frac{V\cdot \rho_{Fl}\cdot g}{A} \\ & = & \displaystyle\frac{\cancel{A}\cdot h\cdot \rho_{Fl}\cdot g}{\cancel{A}} \\ & = & h\cdot \rho_{Fl}\cdot g \\ \end{array} \]
15.3.3 Kommunizierende Gefäße
Nach der Formel für den hydrostatischen Druck hängt der Bodendruck eines Gefäßes ausschließlich von der Höhe der Flüssigkeitssäule ab. Werden Gefäße unterschiedlicher Form (Kommunizierende Gefäße (engl. communicating vessels)) untereinander verbunden, so bildet sich in allen Gefäßen derselbe Flüssigkeitspegel waagrecht zur Erdoberfläche aus und bestätigt die Formel für den hydrostatischen Druck (Bild 15.14).
Dass die Wassermenge in den einzelnen Gefäßen dabei keine Rolle spielt, erscheint auf den ersten Blick paradox, deshalb wird es hydrostatisches Paradoxon genannt. Wären die Säulen Festkörper, wäre der Bodendruck tatsächlich abhängig von der Menge des Materials. Hier handelt es sich aber um eine Flüssigkeit, die auch Druck an die Gefäßwände ableiten kann.
Im Bild 15.15 oben siehst du die verbundenen Gefäße in einem Wassertank. Die Formen haben Löcher, und die Flüssigkeit kann überallhin eindringen. Wir warten, bis die Flüssigkeit ruht. Jetzt schließen wir alle Löcher (Bild 15.15 Mitte). Ob die Löcher da sind oder nicht, macht für die Flüssigkeit keinen Unterschied, da sich die Flüssigkeitsteilchen ja nicht mehr bewegen. Auf beiden Seiten der Gefäßwände herrscht jeweils der gleiche Wasserdruck – es macht auch keinen Unterschied, ob die Wände der kommunizierenden Gefäße flexibel oder starr sind. Jetzt wird die umgebende Flüssigkeit im Wassertank abgelassen (Bild 15.15 unten). Die Flüssigkeit in den verbundenen Gefäßen ist davon unbeeinflusst. Der nun fehlende Druck auf der Außenseite der Gefäße wird von den Gefäßwänden aufgebracht.
15.3.4 Anwendungen kommunizierender Gefäße
Die wohl häufigste Anwendung kommunizierender Gefäße findest du gleich mehrmals bei dir zu Hause: den Geruchsverschluss (engl. trap). Dabei handelt es sich um ein u-förmiges Rohr unter Wasch- und Spülbecken. Bei jedem Spülvorgang bleibt ein wenig (sauberes) Wasser im Rohr zurück und verhindert, dass die Kanalgerüche in den Wohnraum gelangen (Bild 15.16).
Weitere Anwendungsbeispiele sind:
15.3.5 Atmosphärischer Druck
Auf Meeresniveau herrscht ungefähr ein Luftdruck von \(1\;\textrm{bar}\). Auch dieser Druck ist eine Folge der Gewichtskraft der darüber liegenden Luftmoleküle (Druck in schweren Gasen). Da sich Flüssigkeiten nicht zusammendrücken lassen, ergibt sich für den hydrostatischen Druck eine lineare Gleichung. Im Gegensatz dazu lässt sich Luft – wie alle Gase – zusammendrücken. Der atmosphärische Druck (engl. atmospheric pressure) nimmt mit zunehmender Höhe nicht linear ab.
Unter der Annahme einer konstanten Temperatur in allen Luftschichten lässt sich mithilfe der Integralrechnung die barometrische Höhenformel herleiten. Nach der barometrischen Höhenformel nimmt der Druck mit der Höhe exponentiell ab (Bild 15.17).
Und wo hört jetzt die Atmosphäre auf und wo beginnt der Weltraum? Eine natürliche Grenze gibt es nicht. Die Atmosphäre wird einfach immer dünner, je weiter du dich von der Erde entfernst. Üblicherweise wird eine Höhe von \(100\;\mathrm{km}\) über dem Meeresspiegel als Grenze angegeben (Kármán-Linie). Ab dieser Höhe gibt es keinen nennenswerten aerodynamischen Auftrieb mehr und Flügel werden nutzlos. Hier endet die Luftfahrt und die Raumfahrt beginnt.
15.3.6 Magdeburger Halbkugeln
Mitte des 17. Jahrhunderts demonstrierte Otto von Guericke mit dem spektakulären Versuch der Magdeburger Halbkugeln (engl. Magdeburg hemispheres) die Wirkung des Luftdrucks. Dabei verwendete er zwei Halbkugeln aus Metall. Mit einer „umgekehrten“ Luftpumpe entfernte er einen Großteil der Luft aus der Kugel (Bild 15.18 a). Nicht nur, dass die zwei Hälften aufgrund der Druckdifferenz von allein zusammenblieben; selbst zwei Gespanne mit je acht Pferden schafften es nicht, die beiden Hälften zu trennen!
Das ist wirklich erstaunlich. Berechnen wir die Kraft, die die Pferde überwinden müssen. Für unsere Überlegungen gehen wir von einem normalen Luftdruck (\(p = 1\;\mathrm{bar} = 1\cdot 10^{5}\;\mathrm{Pa}\)) auf der Außenseite und einem perfekten Vakuum (\(p = 0\)) auf der Innenseite aus. Für das Trennen der Hälften müssen nur die waagrechten Kräfte berücksichtigt werden. Ersetzen wir die Kugelhälften durch Zylinderhälften, ändert das nichts am Ergebnis, aber alle Kraftpfeile sind jetzt parallel oder normal zur Zugrichtung der Seile (Bild 15.18 b)) und wir können die Kraft leichter berechnen. Die waagrechten Pfeile entsprechen der Kraft auf Grund- und Deckfläche des Zylinders. Bei einem Durchmesser von \(d = 42\;\mathrm{cm} = 0{,}42\;\mathrm{m}\) erhalten wir eine Querschnittsfläche von:
\[ A=\pi r^{2}={\frac {\pi d^{2}}{4}} = 0{,}13\ldots\;\mathrm{m^2} \]
Und für die Druckkraft von beiden Seiten:
\[ F = 2\cdot p\cdot A = 27\,708{,}85\;\mathrm{N} \]
Die Zugkraft eines durchschnittlichen Pferdes beträgt in etwa \(1\,200\;\mathrm{N}\). Bei 16 Pferden ergibt das eine Gesamtkraft von \(16 \cdot 1\,200 = 19\,200\;\mathrm{N}\). Diese Kraft reicht nicht aus, die Druckkraft durch den Luftdruck auf die Hälften zu überwinden.
15.3.7 Pumpen
Pumpen können zum Heben von Wasser verwendet werden. Dabei gibt es zwei unterschiedliche Möglichkeiten.
- Druckpumpen (arbeiten mit Überdruck)
- Saugpumpen (arbeiten mit Unterdruck)
In Bild 15.19 siehst du die Funktionsweise einer Druckpumpe (engl. pressure pump). Die Pumpe befindet sich in unmittelbarer Nähe oder sogar in dem Wasserreservoir (Tauchpumpe). Wird der Kolben gehoben (a) öffnet sich das Bodenventil und Wasser strömt in den Pumpenraum. Wird der Kolben nach unten gedrückt (b), schließt sich das Bodenventil und das Ventil im Steigrohr öffnet sich. Erzeugt der Kolben einen Druck größer als den Schweredruck der Wassersäule im Steigrohr, wird das Wasser nach oben geschoben.
Bei einer Saugpumpe (engl. suction pump) befindet sich die Pumpe beim Auslass (Bild 15.20). Wird der Kolben nach unten verschoben, öffnet sich das Ventil am Kolben und das Wasser unterhalb des Kolbens strömt in den Raum darüber. Wird der Kolben gehoben, schließt sich das Ventil am Kolben und das Wasser wird aus dem Pumpenzylinder entfernt. Gleichzeitig schiebt der Umgebungsdruck Wasser über das Steigrohr in den nun leeren Raum im Pumpenzylinder nach. Da bei Saugpumpen der Umgebungsdruck die Wassersäule heben muss, funktionieren solche Pumpen nur dann, wenn der Schweredruck der Wassersäule kleiner als der Luftdruck ist. Auf der Erde entspricht das einer Wassersäule von rund \(10\;\mathrm{m}\). Aus größeren Tiefen kann Wasser daher nur mit einer Druckpumpe heraufbefördert werden.
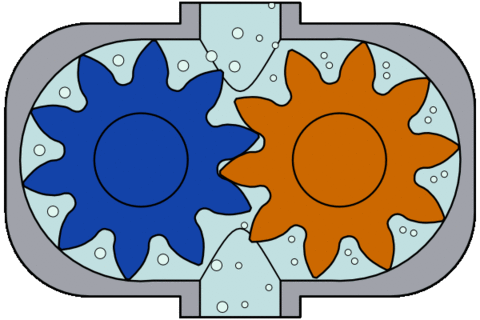
In den bisher gezeigten Beispielen erfolgt die Wasserverdrängung durch einen Kolben, der sich hebt und senkt. In elektrischen Pumpen wird das Wasser meist durch rotierende Zahnräder oder Kolben verdrängt (Bild 15.21). Eine Zahnrad- (engl. gear pump) oder Drehkolbenpumpe (engl. lobe pump) benötigt für den Betrieb keine Ventile.
Eine ebenfalls weitverbreitete Pumpe ist die Kreisel- oder Zentrifugalpumpe (engl. centrifugal pump). Das rote Schaufelrad in Bild 15.22 versetzt das waagrecht zufließende Wasser in Drehung. Das schnell rotierende Wasser bewegt sich aufgrund der Zentrifugalkraft an den Rand des Schaufelrades, wo es durch eine Austrittsöffnung das Gehäuse mit der Tangentialgeschwindigkeit nach oben verlässt – es wird sozusagen nach oben geschleudert.
15.3.8 Saugheber
Willst du ein Gefäß mit Flüssigkeit entleeren, musst du es weder umkippen noch ein Loch in dessen Boden bohren. Mit einem Saugheber (engl. siphon vom altgriechischen σίφων für „Heber“) geht das fast von allein. Nimm einen Schlauch, halte ihn in die Flüssigkeit und sauge die Flüssigkeit bis zu deinem Mund. Wenn du das Schlauchende aus dem Mund nimmst, achte darauf, dass es sich unterhalb des Gefäßbodens befindet. Befindet sich der Schlauchanfang am Boden des Gefäßes, läuft die Flüssigkeit vollständig aus!
Wie der Saugheber funktioniert, kannst du anhand des Bildes 15.23 erkennen. Bis auf die unterschiedlich hohen Flüssigkeitssäulen links und rechts im Rohr (schraffierte Bereiche) gibt es keinen Unterschied zwischen beiden Seiten. Darin muss der „Motor“ für die Bewegung der Flüssigkeit enthalten sein.
Während die Flüssigkeit im Rohr fließt, sperren wir die Verbindung mit einem Ventil ab und überlegen uns die Drücke \(p_1\) und \(p_2\) auf beiden Seiten des Ventils. Auf die Oberflächen beider Flüssigkeiten wirkt der gleiche Umgebungsdruck \(p_0\). Der Schweredruck der jeweiligen Wassersäule verringert den Druck auf beiden Seiten des Ventils. Da die Wassersäule im tiefer liegenden Behälter aber höher ist, wird dort der Luftdruck mehr vermindert; \(p_2\) ist somit kleiner als \(p_1\) (\(p_2 < p_1\)). Öffnen wir das Ventil, verschiebt sich die Flüssigkeit in Richtung des kleineren Drucks.
Für die einzelnen Drücke gilt:
\[ p_1 = p_0 - \rho\cdot g\cdot h_1 \]
und
\[ p_2 = p_0 - \rho\cdot g\cdot h_2 \]
Für die Druckdifferenz erhalten wir
\[ \begin{aligned} \Delta p = {} & p_1 - p_2 \\ = {} & (p_0-\rho\cdot g\cdot h_1) - (p_0-\rho\cdot g\cdot h_2) \\ = {} & p_0-\rho\cdot g\cdot h_1 - p_0 + \rho\cdot g\cdot h_2 \\ = {} & \rho\cdot g\cdot h_2 - \rho\cdot g\cdot h_1 \\ = {} & \rho\cdot g\cdot (h_2-h_1) \\ = {} & \rho\cdot g\cdot h \\ \end{aligned} \]
mit \(\rho\) der Dichte der Flüssigkeit, \(g\) der Fallbeschleunigung und \(h\) der Höhendifferenz zwischen den beiden Flüssigkeitsoberflächen. Je größer die Druckdifferenz, desto schneller fließt die Flüssigkeit in das tiefer liegende Gefäß.
15.3.9 Pythagoreischer Becher
Die Konstruktion des Pythagoreischen Bechers (engl. pythagoras cup) wird Pythagoras von Samos zugeschrieben. Angeblich wurde der Becher entworfen, um seinen Besitzer maßvolles Nachschenken zu lehren. Sobald der Füllstand die strichlierte Linie in Bild 15.24 übersteigt, leert sich der Becher vollständig.
Der Pythagoreische Becher funktioniert nach dem Prinzip des Saughebers. Mit dem Einschenken steigt der Pegel der Flüssigkeit auch im Kanal in der Mitte an (kommunizierender Gefäße). Kann das Wasser schließlich in der Mitte überfließen, sorgt der Unterschied des Schweredrucks der beiden Wassersäulen (schraffierte Bereiche) für das vollständige Auslaufen der Flüssigkeit.
Links: