7.8 Rotierende Bezugssysteme
Bist du Teil eines rotierenden Systems (Bild 7.56), verhalten sich Körper darin oft unerwartet.
Im Teil über Bewegungslehre hast du schon etwas über Inertialsysteme (unbeschleunigte Bezugssysteme) erfahren. Im Kräfte-Teil hast du erfahren, dass in einem beschleunigten Bezugssystem sogenannte Scheinkräfte verwendet werden, um die gemessenen Beschleunigungen mithilfe der Newtonschen Gesetze weiterhin beschreiben zu können.
In diesem Kapitel geht es um rotierende Bezugssysteme, die – nachdem jede Rotation einer Beschleunigung entspricht – auch beschleunigte Bezugssysteme sind.
7.8.1 Ein einfaches rotierendes Bezugssystem
In Bild 7.57 siehst du eine einfache Methode, wie du dir selbst ein rotierendes Bezugssystem bauen kannst.
Dazu hängst du ein Smartphone über einer ebenen Tischplatte (dein Inertialsystem (oder unbeschleunigtes Bezugssystem)) an einer Schnur auf. Filmst du die Bewegung von Körpern auf dem Tisch mit der Kamera, während sich das Smartphone dreht, siehst du die Bewegung aus der Sicht eines rotierenden Bezugssystems.
Verwendest du eine sehr dünne und lange Schnur für die Aufhängung, kannst du ein recht gutes gleichförmig rotierendes Bezugssystem erzeugen. Wählst du hingegen eine dicke Schnur, verdrillst sie und lässt sie los, erhältst du ein rotations-beschleunigtes Bezugssystem.
7.8.2 Was ist eine Scheinkraft?
Wir filmen mit einer gleichförmig rotierenden Kamera eine Kugel, die ruhig auf einem Tisch liegt. In dem Video siehst du, wie die – im Inertialsystem ruhende – Kugel eine Kreisbahn beschreibt (Bild 7.58).
Jede Bewegung auf einer Kreisbahn ist beschleunigt. Da im Inertialsystem „Tisch“ die Kugel ruht und keine Kraft (in der Tischebene) auf sie wirkt, kann die im rotierenden Bezugssystem beobachtete Beschleunigung nicht die Folge einer Kraft sein, sondern ist lediglich eine Folge unserer „ungewöhnlichen“ Wahl des Bezugssystems.
Das dynamische Grundgesetz, nachdem die Ursache für jede Beschleunigung eine Kraft ist, gilt nur in Inertialsystemen. Führen wir für das rotierende Bezugssystem fiktive oder Scheinkräfte ein, lässt sich das Auftreten dieser zusätzlichen Beschleunigungen über diese (Schein-)Kräfte „erklären“ und wir können mit ihrer Hilfe die newtonschen Gesetze auch in diesem Bezugssystem verwenden.
Aber Vorsicht: Durch das Einführen von Scheinkräften kann nicht alles „repariert“ werden! Zum Beispiel gelten Impuls- und Energieerhaltungssatz in einem beschleunigten Bezugssystem trotz Einführung von Scheinkräften nicht mehr.
Auch wenn sie „Schein“kräfte heißen: Sobald sich eine Person in einem rotierenden Bezugssystem befindet, spürt sie selbstverständlich ihre Auswirkung!
In einem rotierenden Bezugssystem können maximal drei Scheinkräfte auftreten, die in Summe für die – nur in diesem Bezugssystem auftretenden – Beschleunigungen aufkommen:
- Zentrifugalkraft (eine vom Ort des Körpers abhängige Scheinkraft)
- Corioliskraft (eine von der Geschwindigkeit des Körpers abhängige Scheinkraft)
- Eulerkraft (eine von der Winkelbeschleunigung des Bezugssystems abhängige Scheinkraft)
In den folgenden Abschnitten erfährst du mehr über die Eigenschaften dieser drei Scheinkräfte.
7.8.3 Kreispendel und synchron rotierende Kamera
Bei einem idealen Kreispendel bleibt der Pendelkörper immer auf derselben Höhe und beschreibt im Inertialsystem eine Kreisbahn. Im Gegensatz zu unserem letzten Beispiel gibt es jetzt auch eine Beschleunigung im Inertialsystem des Tisches, die durch die Zugkraft des Fadens hervorgerufen wird – nämlich die Zentripetalkraft, die den Pendelkörper auf die Kreisbahn zwingt.
Wählen wir für das rotierende Bezugssystem dieselbe Winkelgeschwindigkeit wie die des Kreispendels, sehen wir auf dem Film keine Bewegung (Bild 7.59)! Damit es im rotierenden Bezugssystem zu keiner Beschleunigung kommt, muss die zum Zentrum gerichtete Zentripetalkraft \(F_\text{Zp}\) des Fadens durch eine gleich große Scheinkraft ausgeglichen werden, die in die entgegengesetzte Richtung zeigt. Diese Kraft wird Zentrifugalkraft \(F_\text{Zf}\) genannt.
Ruht ein Körper im rotierenden Bezugssystem, gilt:
\[ F_\text{Zf} = -F_\text{Zp} \]
In diesem Fall können wir eine dynamische Situation im Inertialsystem durch eine statische Situation im rotierenden Bezugssystem beschreiben. Dieser spezielle Fall ist die häufigste Anwendung für die Verwendung eines rotierenden Bezugssystems!
7.8.4 Zentrifugalkraft
Auf jeden Körper in einem rotierenden Bezugssystem wirkt immer eine vom Drehzentrum weg gerichtete Zentrifugalkraft (engl. centrifugal force). Das Wort „zentrifugal“ kommt von centrum, dem lateinischen Wort für „Mittelpunkt“ und fugere, dem lateinischen Wort für „fliehen“. Die Größe der Zentrifugalkraft ist:
| \[\begin{equation} F_\text{Zf}=m\cdot r\cdot\omega^{2} \tag{7.23} \end{equation}\] |
Die Symbole darin bedeuten:
- \(F_\text{Zf}\), die Zentrifugalkraft auf einen Körper in einem rotierenden Bezugssystem (in \(\mathrm{N}\))
- \(m\), Masse des Körpers (in \(\mathrm{kg}\))
- \(\omega\), die Winkelgeschwindigkeit des rotierenden Bezugssystems relativ zum Inertialsystem (in \(\mathrm{rad/s}\))
- \(r\), der Abstand des Körpers zur Drehachse des rotierenden Bezugssystems (in \(\mathrm{m}\))
Aus der Formel kannst du sehen, dass die Größe der Zentrifugalkraft nur von dem Ort (Entfernung zur Drehachse) abhängt (Bild 7.60) und unabhängig von ihrem Bewegungszustand (daher, ob sie – relativ zum rotierenden Bezugssystem – ruht oder sich bewegt) ist.
7.8.5 Herleitung Zentrifugalkraft
Im Spezialfall eines im rotierenden Bezugssystem in Ruhe befindlichen Körpers heben sich Zentrifugalkraft und Zentripetalkraft genau auf. Daher müssen beide Kräfte in diesem Fall entgegengesetzt gleich groß sein. Beginnen wir mit der Gleichung für die Zentripetalkraft (4.11):
\[ |F_\text{Zf}| = |F_\text{Zp}| = \frac{m\cdot v^2}{r} \]
Drücken wir die Bahngeschwindigkeit \(v\) durch die Winkelgeschwindigkeit \(\omega\) aus, erhalten wir:
\[\begin{align} |F_\text{Zf}| = {} & \frac{m\cdot (r\cdot\omega)^2}{r} \\ = {} & \frac{m\cdot r^\cancel{2}\cdot\omega^2}{\cancel{r}} \\ = {} & m \cdot r \cdot\omega^2 \\ \end{align}\]
Beachte: In diesem Fall ist die Winkelgeschwindigkeit von Körper und rotierendem Bezugssystem gleich groß. Für die Berechnung der Zentrifugalkraft ist immer die Winkelgeschwindigkeit des Bezugssystems einzusetzen!
7.8.6 Ebenes Pendel und rotierende Kamera
In unserem nächsten Beispiel filmen wir ein ebenes Pendel mit einer rotierenden Kamera (Bild 7.61).
Im Film beobachten wir zunächst eine Drehung der Pendelebene in die entgegengesetzte Richtung zur Drehrichtung der Kamera. Dadurch sehen wir neben der rücktreibenden Beschleunigung eine weitere Beschleunigung, die den Pendelkörper immer rechts zu seiner Bewegungsrichtung ablenkt, sodass auf dem Video eine Rosettenbahn zu sehen ist.
Diese Beschleunigung quer zur Bewegungsrichtung beschreiben wir durch eine weitere Scheinkraft, die Corioliskraft.
7.8.7 Abschätzung der Corioliskraft
Wir möchten die Größe der Corioliskraft abschätzen. Dazu rollen wir eine Kugel aus der Mitte des Tisches an den Rand. Vernachlässigen wir die Reibung, wirken im Inertialsystem des Tisches nach dem Anstoßen keine Kräfte mehr auf die Kugel und sie bewegt sich mit konstanter Geschwindigkeit \(v\) entlang einer geraden Bahn (Bild 7.62, links). In der Zeit \(t\) legt sie dabei eine Strecke \(r=v\cdot t\) zurück.
Wechseln wir in das rotierende Bezugssystem; einer mit der Winkelgeschwindigkeit \(\omega\) nach links drehenden Kamera über dem Tisch (Bild 7.62, rechts). Bezogen auf dieses Bezugssystem weicht die Kugel nach rechts von der geraden Richtung ab. Der Tisch hat sich dabei um den Winkel \(\varphi = \omega\cdot t\) nach rechts weitergedreht. Die seitliche Abweichung \(d\) der Kugel ist dann in der Größenordnung von
\[ d = r\cdot \varphi = r\cdot \omega\cdot t \]
Drücken wir die Strecke \(r\) durch die Zeit aus (\(r=v\cdot t\)) erhalten wir:
\[ d = v\cdot t \cdot \omega\cdot t = v\cdot \omega\cdot t^2 \]
Die Abweichung \(d\) ist also proportional zu \(t^2\) (\(d\propto t^2\)). Das entspricht einer gleichmäßig beschleunigten Bewegung. Für den zurückgelegten Weg bei dieser Bewegungsform gilt (Gleichung (3.7)):
\[ s = \frac{a\cdot t^2}{2} \]
Setzen wir beide Längen gleich, erhalten wir einen Ausdruck für die Coriolis-Beschleunigung:
\[ \begin{aligned} s = {} & d \\ \frac{a\cdot t^2}{2} = {} & v\cdot \omega\cdot t^2 &&\qquad\Bigr\rvert\cdot \frac{2}{t^2} \\ a = {} & 2\cdot v\cdot \omega \\ \end{aligned} \]
Multiplizieren wir den Ausdruck mit der Masse \(m\), erhalten wir daraus den Betrag der Corioliskraft:
\[ F_\text{Co} = m\cdot a = 2\cdot m\cdot \omega\cdot v \]
7.8.8 Corioliskraft
Bewegt sich ein Körper in einem rotierenden Bezugssystem, tritt neben der Zentrifugalkraft eine zweite, geschwindigkeitsabhängige Scheinkraft auf. Diese nach Gaspard Gustave de Coriolis benannte Corioliskraft (Audio abspielen engl. coriolis force) auf. Ihre Größe ist:
| \[\begin{equation} F_\text{Co}= 2\cdot m\cdot \omega\cdot v \tag{7.24} \end{equation}\] |
Die Symbole darin bedeuten:
- \(F_\text{C}\), die Corioliskraft in einem rotierenden Bezugssystem (in \(\mathrm{N}\))
- \(m\), Masse des Körpers (in \(\mathrm{kg}\))
- \(\omega\), die Winkelgeschwindigkeit des rotierenden Bezugssystems relativ zum Inertialsystem (in \(\mathrm{rad/s}\))
- \(v\), die Geschwindigkeit des Körpers relativ zu dem rotierenden Bezugssystem (in \(\mathrm{m/s}\))
Die Corioliskraft hat folgende Eigenschaften (die sich aus ihrer Vektordefinition ergeben):
- Die Corioliskraft steht immer normal auf den Winkelgeschwindigkeitsvektor \(\vec{\omega}\) des rotierenden Bezugssystems und den Geschwindigkeitsvektor \(\vec{v}\).
- Verläuft die Bewegung parallel zur Drehachse, ist die Corioliskraft null.
- Steht der Geschwindigkeitsvektor normal zur Drehachse, ist die Corioliskraft maximal.
Rotiert das Bezugssystem gegen den Uhrzeigersinn, lenkt die Corioliskraft den Körper immer nach rechts ab (Bild 7.63). Rotiert das Bezugssystem im Uhrzeigersinn, lenkt die Corioliskraft den Körper immer nach links ab.
Da die Corioliskraft immer normal zur Geschwindigkeitsrichtung steht, lenkt sie den Körper nur ab (ändert seine Richtung), ohne dabei seine Schnelligkeit zu ändern.
7.8.9 Foucaultsches Pendel
Auf der Erde sehen wir die vollständige Drehung des Sternenhimmels im Laufe eines Tages. Aber beweist das, dass sich die Erde dreht? Könnte sich nicht die Himmelskugel um die Erde drehen? Einen anschaulichen Beweis der Erddrehung lieferte um 1850 erstmals das Foucaultsches Pendel (Audio abspielen, engl. Foucault pendulum) benannt nach Léon Foucault. Dabei handelt es sich um ein ganz gewöhnliches Pendel mit besonders langer Seillänge (Bild 7.64), um Reibung (Lagerreibung, Luftreibung) möglichst zu vermeiden.
Bild 7.64: Foucaultsches Pendel im Panthéon (Paris, Frankreich)
Wirkt nur die Schwerkraft auf ein Pendel, bleibt die Schwingungsebene des Pendelkörpers relativ zum Sternenhimmel unverändert (Inertialsystem). In Bild 7.65 siehst du ein Pendel am Nordpol. Da sich die Erde unter dem Pendel hinwegdreht, sieht eine Person auf der rotierenden Erde eine scheinbare Drehung der Pendelebene um 360° innerhalb eines Tages (analog zum Sternenhimmel). Die Bahnkurve ist eine Rosette, die du schon aus Abschnitt kennst.
Wesentlich komplizierter wird die Sache, wenn sich das Pendel nicht an einem der beiden Pole befindet, sondern an einer anderen Stelle auf der Erde (Bild 7.66). Denn jetzt bewegt sich der Aufhängepunkt des Pendels auf einer Kreisbahn um die Erde und die Pendelebene dreht sich relativ zum Sternenhimmel (Inertialsystem).
Die auf der Erde zu beobachtende Drehung verlangsamt sich dadurch und ist abhängig vom Breitengrad des Ortes. Die Zeit für eine vollständige Drehung der Schwingungsebene des Pendels kannst du dir mithilfe der folgenden Formel berechnen (ohne Herleitung):
\[ T={\frac {2\pi }{\omega \sin \varphi }} \]
In dieser Formel bedeuten:
- \(T\), die Zeit für eine vollständige Drehung der Schwingungsebene des Pendels (in \(\mathrm{s}\))
- \(\omega\), die Winkelgeschwindigkeit des Planeten (in \(\mathrm{rad/s}\))
- \(\varphi\), der Breitengrad, an dem das Pendel hängt (in \(\mathrm{rad}\))
Besonders interessant sind auch die Verhältnisse am Äquator. Denn obwohl sich dort die Pendelebene ständig (relativ zum Sternenhimmel) dreht, bleibt die Pendelebene aus der Sicht einer Person auf der Erde unverändert! Das liegt daran, dass alle Scheinkräfte am Äquator ausschließlich in der Äquatorebene liegen und daher keine Drehung der Pendelebene bewirken.
Aus der Sicht einer Person auf der Erde dreht sich die Pendelebene auf der Nordhalbkugel nach rechts (im Uhrzeigersinn) und auf der Südhalbkugel nach links (gegen den Uhrzeigersinn).
Jede Drehung der Schwingungsebene (im Inertialsystem) benötigt eine Kraft, die Arbeit an dem Pendelkörper verrichtet. Diese Kraft ist jene Komponente der Gravitation, die im rechten Winkel zur Drehachse steht. Die Energie für die Bahndrehung des Pendels kann letztlich nur von der Rotationsenergie der Erde stammen. Die Änderung der Erdrotation aufgrund der Drehung der Pendelebene bleibt aber wegen des enormen Massenunterschieds unbemerkt. Nur an den Polen ist diese Komponente null, und dort, aber eben nur dort, behält die Schwingungsebene ihre Ausrichtung relativ zu den Sternen bei und die Arbeit für eine Bahndrehung entfällt.
7.8.10 Ablenkung eines fallenden Körpers
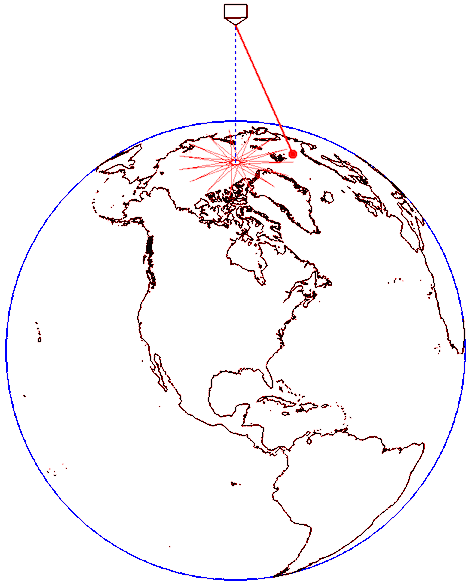
Auch schon vor dem Beweis der Erddrehung durch das Foucaultsches Pendel gab es Überlegungen, wie sich die Erddrehung durch Experimente auf der Erde zeigen ließe. Eine Überlegung dazu lautet: „Lasse ich einen Körper von einem sehr hohen Turm am Äquator fallen, dreht sich während des Falls die Erde mit dem Turm unter dem Körper weiter und so sollte der Körper doch hinter dem Turm zurückbleiben. Betrachten wir die Erde aus Richtung Norden, sollte der Körper nach Westen abgelenkt werden (Bild 7.67).“
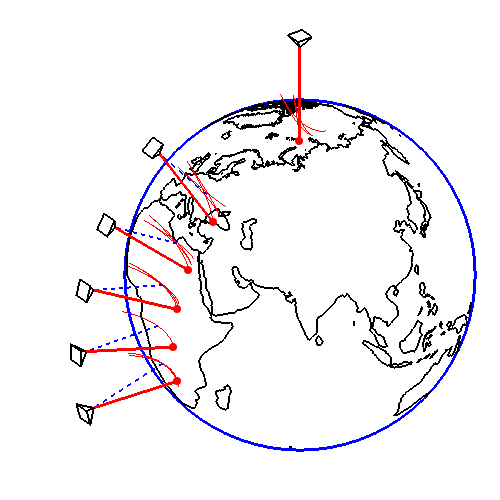
Die Überlegung klingt im ersten Moment plausibel, ist aber falsch! Betrachten wir die Situation zunächst aus der Sicht eines Inertialsystems außerhalb der Erde (Bild 7.68). Bevor der Gegenstand fallen gelassen wird, befindet er sich auf einem Orbit um die Erde und hat eine Bahngeschwindigkeit \(v_0\). Wird der Körper von der Person am Turm losgelassen, entspricht das prinzipiell einem waagrechten Wurf mit der Anfangsgeschwindigkeit \(v_0\). Im Gegensatz zum waagrechten Wurf ändert sich die Beschleunigungsrichtung aber während des Falls geringfügig (sie zeigt ja wie die Gravitationskraft immer zum Massenmittelpunkt). Die Kurve ist daher keine exakte Parabel, aber eine sehr ähnliche Kurve.
Bild 7.68: Ablenkung eines fallenden Körpers von einem hohen Turm unter Berücksichtigung der Erdrotation
Während des Falls wird die Geschwindigkeit größer und auch die Richtung der Geschwindigkeit des Körpers ändert sich ständig. Aber die ursprüngliche Geschwindigkeit \(v_0\) „steckt“ auch noch kurz vor dem Einschlag auf dem Erdboden immer noch in der Gesamtgeschwindigkeit. Vergleichst du die Größe dieser Geschwindigkeit mit der Bahngeschwindigkeit am Fuß des Turmes (sie nimmt linear mit dem Radius ab), erkennst du, dass der fallende Körper nicht zurückbleibt, sondern im Gegenteil, den Turm sogar überholt!
Wie sieht die Situation aus der Sicht des rotierenden Bezugssystems Erde aus? Wird der Körper vom Turm fallen gelassen, hat er in diesem Bezugssystem keine waagrechte Geschwindigkeit (\(v = v_0 = 0\)). Das entspricht einem freien Fall. Allerdings wirkt im rotierenden Bezugssystem zusätzlich zur Gravitation die Corioliskraft, die im rechten Winkel zur Geschwindigkeitsrichtung zeigt und eine seitliche Ablenkung bewirkt. Diese Kraft sorgt dafür, dass der Körper in Richtung Osten beschleunigt den Turm überholt.
Beabsichtigst du, das Experiment selbst durchzuführen, wirst du keine Ablenkung feststellen können. Bei kurzen Fallstrecken ist die Ablenkung einfach zu klein, um sie mit einfachen Mitteln zu messen.
Links:
7.8.11 Wirkung der Corioliskraft auf Luft- und Wassermassen
Die Ursache für großräumige Bewegungen von Luft- und Wassermassen ist in erster Linie der Temperaturunterschied zwischen den unterschiedlichen Stellen auf der Erde. Der damit verbundene Dichteunterschied bewirkt eine Strömung von dichteren Stellen zu Stellen mit geringerer Dichte.
Aber es gibt noch einen zweiten Effekt, der die Bewegung der Atmosphäre und der Ozeane beeinflusst. Unsere Erde dreht sich von West nach Ost (im Osten geht die Sonne auf). Die Tangentialgeschwindigkeit auf einer rotierenden Kugel ist aber nicht überall gleich groß, sondern ändert sich mit dem Breitengrad. Durch Reibung passt sich die Bewegung der Luft- und Wassermassen der Tangentialgeschwindigkeit am jeweiligen Ort allmählich an.
Der Passatwind ist ein sehr beständiger Wind, der nahe dem Äquator auftritt (Bild 7.69). Dabei fällt auf, dass die zum Äquator strömenden Passatwinde auf der Nordhalbkugel nach rechts (Nordost-Passat) und auf der Südhalbkugel (Südost-Passat) nach links abgelenkt werden. Die Bahngeschwindigkeit am Äquator ist stets größer als bei größeren Breitengraden. Kommt der Wind aus einer solchen Region, ist seine horizontale Geschwindigkeit zunächst kleiner als die am Äquator und fällt bezüglich der Erde zurück.
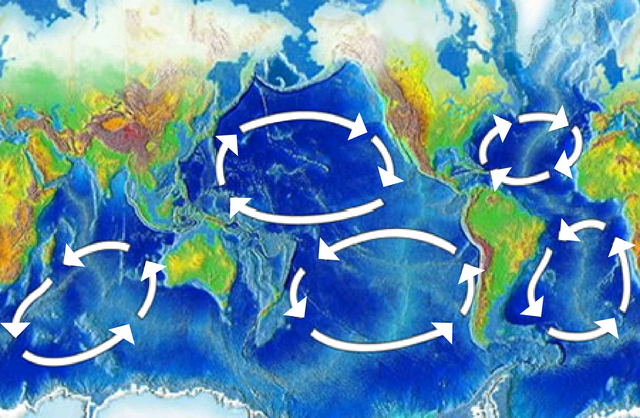
Dasselbe Verhalten – unterschiedlicher Drehsinn auf beiden Hemisphären – ist auch bei den fünf großräumigen Wirbeln der Ozeane (engl. gyre) zu beobachten (Bild 7.70).
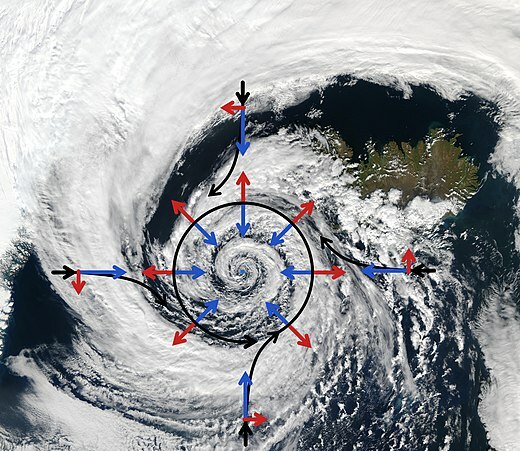
Bild 7.71: Tiefdruckgebiet über Island (Nördliche Halbkugel, blaue Pfeile: Druckkraft, rote Pfeile: Corioliskraft )
Wir, die wir uns im rotierenden Bezugssystem Erde befinden, beobachten keine Tangentialgeschwindigkeit. Die Ablenkung der Luft- und Wassermassen in Ost-West-Richtung beschreiben wir durch die Corioliskraft. In Bild 7.71 entsprechen Druckkräfte den blauen Pfeilen und die Corioliskraft, die immer senkrecht zur Geschwindigkeitsrichtung steht, durch rote Pfeile.
7.8.12 Drehrichtung ablaufenden Wassers
Der Wirbel, der beim Auslassen eines Waschbeckens entsteht (Bild 7.72), hat dieselbe Drehrichtung wie der Luftwirbel in Bild 7.71. Könnte es sein, dass die Drehrichtung des ablaufenden Wassers aufgrund der Corioliskraft auf der Nordhalbkugel immer linksdrehend und auf der Südhalbkugel immer rechtsdrehend ist?
Das wurde in vielen Experimenten widerlegt! Es ist zwar richtig, dass auch auf die Flüssigkeitsteilchen im Waschbecken die Corioliskraft wirkt. Aber ihre Wirkung ist vernachlässigbar klein im Verhältnis zu anderen Einflussgrößen, wie der Form des Beckens, die Geometrie des Abflusses oder wie das Becken befüllt wurde. Die Corioliskraft spielt in diesem Maßstab keine Rolle.
7.8.13 Eötvös-Effekt
Die Gravitation sorgt auf der Erdoberfläche für die Gewichtskraft. Zusätzlich dreht sich die Erde um die eigene Achse. In Bild 7.73 (links) siehst du die Situation aus der Sicht eines Inertialsystems für eine Lokomotive dargestellt, die am Äquator auf den Schienen steht. Wir blicken dabei „von oben“ auf die Erde und sehen den Nordpol.
Aus der Sicht des Inertialsystems bewegt sich der Zug mit derselben Winkelgeschwindigkeit wie die Erde und beschreibt daher eine Kreisbahn um diese. Für jede Kreisbahn ist eine Zentripetalkraft nötig, die den Körper auf seiner Kreisbahn hält. Die Gewichtskraft reduziert sich dabei um diese Zentripetalkraft. Diese um die Zentripetalkraft reduzierte Gravitationskraft wird als Schwerkraft_ (engl. apparent gravity oder effective gravity) bezeichnet. Da der Unterschied im Fall der Erde relativ gering ist (Am Äquator rund \(4\,\%\)), verwenden die meisten Menschen beide Begriffe synonym.
In dem Bild in der Mitte bewegt sich der Zug ostwärts (also in Drehrichtung der Erde). Die Bahngeschwindigkeit des Zuges erhöht sich. Je größer der Anteil der Gravitationskraft wird, der für die Zentripetalkraft aufgewendet werden muss, desto geringer wird der Anteil, der für die Gewichtskraft übrig ist. Der Zug wird in diesem Fall „leichter“.
Im Bild rechts bewegt sich der Zug westwärts (also gegen die Drehrichtung der Erde). Die Bahngeschwindigkeit sinkt und damit auch die nötige Zentripetalkraft. Es bleibt mehr von der Gravitationskraft für die Gewichtskraft übrig. Der Zug lastet jetzt schwerer auf den Schienen! Gleicht die Bewegung des Zuges die Erdrotation gerade aus, steht der Zug im Raum still und es ist überhaupt keine Zentripetalkraft notwendig. Jetzt wirkt die vollständige Gravitationskraft als Gewichtskraft. Erst wenn der Zug noch schneller westwärts fährt, ist wieder eine Zentripetalkraft notwendig und die Gewichtskraft nimmt wieder ab.
Bild 7.74: Änderung der Fallbeschleunigung in Abhängigkeit von der Geschwindigkeit entlang des Äquators
In Bild 7.74 siehst du die Änderung der Fallbeschleunigung in Abhängigkeit von der Geschwindigkeit entlang des Äquators in einem Diagramm zusammengefasst. Dass die Gewichtskraft auf der Erde bei einer Bewegung Richtung Osten abnimmt und Richtung Westen (zunächst) zunimmt, wird nach Loránd Eötvös als Eötvös-Effekt (engl. Eötvös effect) bezeichnet.
Große praktische Bedeutung hat dieser Effekt hauptsächlich beim Start von Raumfahrzeugen. Die schnellste und treibstoffsparendste Möglichkeit in die Umlaufbahn zu gelangen, ist ein Start am Äquator mit einer Flugbahn direkt nach Osten.
7.8.14 Rechenbeispiel zum Eötvös-Effekt
Eine Person mit der Masse \(100\;\mathrm{kg}\) läuft am Äquator mit der Geschwindigkeit \(1\;\mathrm{m/s}\) (\(3{,}6\;\mathrm{km/h}\)). Der Erdradius am Äquator beträgt \(6368\;\mathrm{km}\) und die Fallbeschleunigung \(9.79\;\mathrm{m/s^2}\). Berechne die scheinbare Massenabnahme aufgrund des Eötvös-Effekts, wenn sie nach Osten und die scheinbare Massenzunahme, wenn sie nach Westen läuft.
Für unsere Berechnung wählen wir ein Inertialsystem (Fixsternhimmel). Bei der Drehung der Erde um ihre Achse gehen wir von einer Periodendauer von \(24\) Stunden (\(=24\cdot 60\cdot 60 = 8.64\cdot 10^{4}\;\mathrm{s}\)) aus. Dann erhalten wir für eine am Äquator sitzende Person eine Bahngeschwindigkeit von:
\[\begin{eqnarray} v & = & \frac{2\pi\cdot r}{T} \notag \\ & = & \frac{2\pi\cdot 6.368\cdot 10^{6}\;\mathrm{m}}{8.64\cdot 10^{4}\;\mathrm{s}} \notag \\ & = & 463.0940282\;\mathrm{m/s} \notag \\ \end{eqnarray}\]
Läuft die Person nach Osten (in Drehrichtung der Erde), erhöht sich die Bahngeschwindigkeit um die Laufgeschwindigkeit:
\[ v_\text{Ost} = 463{,}09\ldots + 1 = 464{,}09\ldots\;\mathrm{m/s} \]
Bewegt sie sich nach Westen (gegen die Drehrichtung der Erde), reduziert sich die Bahngeschwindigkeit um die Laufgeschwindigkeit:
\[ v_\text{West} = 463{,}09\ldots - 1 = 462{,}09\ldots\;\mathrm{m/s} \]
Für diese drei Geschwindigkeiten erhalten wir die folgenden Zentripetalkräfte:
\[\begin{eqnarray} F = {} & \frac{m\cdot v^2}{r} = 3{,}36\ldots \;\mathrm{N} \notag \\ F_\text{Ost} = {} & \frac{m\cdot v_\text{Ost}^2}{r} = 3{,}38\ldots\;\mathrm{N} \notag \\ F_\text{West} = {} & \frac{m\cdot v_\text{West}^2}{r} = 3{,}35\ldots\;\mathrm{N} \notag \\ \end{eqnarray}\]
Für die Differenz dieser Kräfte zum sitzenden Fall erhalten wir:
\[\begin{eqnarray} \Delta F_\text{Ost} = {} & F_\text{Ost} - F = 0{,}014\ldots\;\mathrm{N} \notag \\ \Delta F_\text{West} = {} & F_\text{West} - F = -0{,}014\ldots\;\mathrm{N} \notag \\ \end{eqnarray}\]
Diese Abweichungen von der Gewichtskraft werden von einer Waage, die mit dem Ortsfaktor \(g = 9.79\;\mathrm{m/s^2}\) geeicht wurde, als folgende scheinbare Massenänderung angezeigt:
\[\begin{eqnarray} \Delta m_\text{Ost} = {} & \frac{\Delta F_\text{Ost}}{g} = 0{,}0014\ldots\;\mathrm{kg} = 1{,}48\ldots\;\mathrm{g} \notag \\ \Delta m_\text{West} = {} & \frac{\Delta F_\text{West}}{g} = -0{,}0014\ldots\;\mathrm{kg} = -1{,}48\ldots\;\mathrm{g} \notag \\ \end{eqnarray}\]
Die Abweichungen sind zwar so klein, dass sie für eine Person nicht zu spüren sind, aber durchaus in einer Größenordnung, die mechanische Gravimeter feststellen können.
Übrigens: Dieses Beispiel stammt aus dem Artikel „Experimenteller Nachweis der Schwereänderung, die ein auf normal geformter Erdoberfläche in östlicher oder westlicher Richtung bewegter Körper durch diese Bewegung erleidet.“ von Roland Eötvös höchstpersönlich (Annalen der Physik Band 59, 1919, S. 744–745)
7.8.15 Eulerkraft
Bisher sind wir stets von einem gleichförmig rotierenden Bezugssystem (daher einer Drehung mit konstanter Winkelgeschwindigkeit) ausgegangen. In einem rotierendem Bezugssystem, dessen Winkelgeschwindigkeit sich mit der Zeit ändert, tritt eine zusätzliche Beschleunigung auf, die durch eine dritte Scheinkraft erklärt werden kann. Diese Kraft wird nach Leonhard Euler als Eulerkraft (engl. Euler force) bezeichnet. Ihre Größe ist (ohne Herleitung):
| \[\begin{equation} F_\text{Eu}=m\cdot \alpha\cdot r \tag{7.25} \end{equation}\] |
In dieser Formel bedeuten:
- \(F_\text{Eu}\), die Eulerkraft (in \(\mathrm{N}\))
- \(m\), Masse des Körpers (in \(\mathrm{kg}\))
- \(\alpha\), die Winkelbeschleunigung des rotierenden Bezugssystems (in \(\mathrm{rad}/\mathrm{s^2}\))
- \(r\), der Abstand der Masse zum Drehzentrum (in \(\mathrm{m}\))
Die Richtung der Eulerkraft steht immer tangential auf den Drehkreis (Bild 7.75).
Da \(a = r\cdot \alpha\) gilt, entspricht die Eulerkraft \(F_\text{Eu}\) in einem rotierenden Bezugssystem, der Trägheitskraft \(F_\text{Tr}\) in einem linear beschleunigten Bezugssystem.
Bist du schon einmal mit einem Karussell gefahren, ist die die Eulerkraft vielleicht schon einmal aufgefallen (Bild 7.76). Ändert sich die Rotationsgeschwindigkeit zum Beispiel beim Anfahren oder beim Anhalten, sorgt die Eulerkraft dafür, dass eine Person (aus der Sicht des rotierenden Bezugssystems „Karussell“) beim Anfahren nach hinten vom Pferd rutscht (und beim Anhalten nach vorne gedrückt wird). Aus der Sicht einer Person außerhalb des Karussells (Inertialsystem) verharrst du beim Anfahren einfach nur in Ruhe und das Karussell dreht sich unter dir hinweg.
7.8.16 Simulierte Schwerkraft
Durch die Aufenthalte an Bord der internationalen Raumstation konnten in den letzten Jahrzehnten viele Erkenntnisse über das Leben in Schwerelosigkeit gewonnen werden. Dabei zeigte sich, dass sich der Körper an die neue Umgebung anpasst und zum Beispiel Muskelmasse abbaut. Für einen längeren Aufenthalt im All wäre es daher wünschenswert, eine Art „künstliche Schwerkraft“ zu haben.
Eine recht einfache Möglichkeit, die Fallbeschleunigung auf der Erde zu simulieren, ist ein rotierendes Bezugssystem. Dabei übernimmt die Zentrifugalkraft die Aufgabe der Gewichtskraft. Denkbar wären ein rotierender Zylinder oder ein rotierender Torus (Ring) (Bild 7.77).
Erfüllt die Rotation die Bedingung
\[\begin{align} F_\text{Z} = {} & F_\text{G} \notag \\ m\cdot\omega^{2}\cdot r = {} & m\cdot g &&\qquad\Bigr\rvert \cdot\frac{1}{m} \notag \\ \omega^{2}\cdot r = {} & g \notag \\ \omega^{2}\cdot r = {} & 9.81\;\mathrm{m/s^2}, \notag \\ \end{align}\]
dann erfahren die Menschen auf der Innenseite der Mantelfläche des Zylinders oder im Inneren des Ringes eine Schwere wie auf der Erdoberfläche in Mitteleuropa.
Könnte eine blinde Person feststellen, ob sie sich auf der Erdoberfläche oder in einem rotierenden Ring befindet? Die Antwort darauf ist: Ja!
Die Zentrifugalkraft ist abhängig von der Entfernung zur Drehachse (Gleichung (7.23)). Stehen wir aufrecht, spürt der Kopf eine andere Kraft als die Füße.
Gehen oder laufen wir in einem rotierenden System, erfahren wir außerdem eine Coriolis-Kraft, die uns zur Seite drängt oder uns leichter oder schwerer werden lässt (Eötvös-Effekt).
Befinden sich Menschen an Bord, wenn die Raumstation erst in Drehung versetzt wird oder ihre Rotationsgeschwindigkeit verlangsamt, wird die Euler-Kraft spürbar.
Diese Effekte verringern sich mit Zunahme des Radius. Wird für die Raumstation ein riesiger Radius gewählt und erst nach Erreichen einer konstanten Rotationsgeschwindigkeit bevölkert, wäre ein schwindelfreies Leben dort durchaus möglich.
Die beste simulierte Schwerkraft erhältst du ganz ohne Rotation: ein mit \(9.81\;\mathrm{m/s^2}\) linear beschleunigtes Raumschiff. Sie wäre von der Schwerebeschleunigung der Erde nicht zu unterscheiden. Das Raumschiff bräuchte dann allerdings einen ständigen Antrieb…
7.8.17 Zentrifugal- und Corioliskraft
Bei Überlegungen in einem rotierenden Bezugssystem sind fast immer mehrere Scheinkräfte zu berücksichtigen. Um dir einen kleinen Eindruck davon zu vermitteln, zeigen wir dir hier zwei Beispiele, wie sich die Scheinkraft aus den Anteilen der Zentrifugal- und Corioliskraft zusammensetzen. Beginnen wir mit der im Inertialsystem Tisch ruhenden Kugel, die du aus dem Kapitelanfang kennst. Die für die Kreisbahn erforderliche Zentripetalkraft ist eine Kombination aus Zentrifugal- und Corioliskraft (Bild 7.78).
Bist du überraschst? Zentrifugal- und Zentripetalkraft haben zwar sehr ähnliche Namen. Das liegt daran, dass beide mit dem Zentrum einer Drehung zu tun haben. Doch abgesehen von ihrem Namen sind Zentrifugal- und Zentripetalkraft im Allgemeinen nie gleich groß! Die einzige Ausnahme ist ein Körper, der in einem gleichförmig rotierenden Bezugssystem ruht (und es zu keiner Corioliskraft kommt, Bild 7.59)!
Als zweites Beispiel betrachten wir ein ebenes Pendel, das sich unter einer rotierenden Kamera befindet. Im Gegensatz zu unserem ersten Beispiel wählen wir dieses Mal eine größere Rotationsgeschwindigkeit der Kamera. Je größer die Drehgeschwindigkeit, desto größer wird die Zentrifugalbeschleunigung. In diesem Fall ist für die Beschreibung der Rosettenbahn eine Kombination aus Faden-, Zentrifugal- und Corioliskraft notwendig (Bild 7.79).
._Darian_is_the_daughter_of_US_Army_(USA)_Sergeant_(SGT)_Ron_B_-_DPLA_-_d6bd1aaf55d8c33689725b29f7b0b700.jpeg){kind=link}
7.8.18 Übersicht Scheinkräfte
So wie jede Bewegung als Superposition von einer translatorischen (geradlinigen) Bewegung und einer Rotation (Drehbewegung) beschrieben werden kann, lässt sich ein allgemein beschleunigtes Bezugssystem als eine Kombination aus einem linear beschleunigten und einem rotierenden Bezugssystem auffassen. In einem allgemein beschleunigten Bezugssystem setzt sich die gesamte Trägheitskraft (Scheinkraft) aus maximal 4 Teilkräften zusammen:
\[\begin{equation} \vec{F}_\text{Sc} = \vec{F}_\text{Tr} + \vec{F}_\text{Zf} + \vec{F}_\text{Co} + \vec{F}_\text{Eu} \tag{7.26} \end{equation}\]
mit den Beiträgen:
- \(\vec{F}_\text{Tr} = m\cdot\vec{a}\quad\) (Trägheitskraft in einem linear beschleunigten Bezugssystem)
- \(\vec{F}_\text{Zf} = m\cdot\vec{\omega}\times(\vec{\omega}\times\vec{r})\quad\) (Zentrifugalkraft)
- \(\vec{F}_\text{Co} = 2\cdot m\cdot(\vec{\omega}\times\vec{v})\quad\) (Corioliskraft)
- \(\vec{F}_\text{Eu} = m\cdot(\vec{\alpha}\times\vec{r})\quad\) (Eulerkraft)
Es sollte dich nicht verwundern, dass alle Scheinkräfte proportional zur Masse sind. Ihre Aufgabe ist es ja gerade, die Effekte der Trägheit (die durch die Masse eines Körpers bestimmt ist) in einem beschleunigten Bezugssystem auszugleichen.