3.2 Geschwindigkeit
In Bild 3.10 siehst du in der Mitte einen Tachometer auf dem Armaturenbrett eines Autos.
In diesem Kapitel beschäftigen wir uns mit dem Geschwindigkeitsbegriff. Du erfährst den Unterschied zwischen Geschwindigkeit und Schnelligkeit und was ein Tachometer genau anzeigt.
3.2.1 Durchschnittsgeschwindigkeit
Fährst du mit einem Fahrzeug (Auto, Fahrrad,…), zeigt dir der Kilometerzähler (engl. odometer) die Länge der Wegstrecke (engl. distance) an, die du während deiner Fahrt zurückgelegt hast. Das Wort „Strecke“ in Wegstrecke ist nicht im mathematischen Sinn zu verstehen - sie muss also nicht notwendigerweise gerade sein. In Bild 3.11 siehst du ein Beispiel für eine Wegstrecke und die Angabe ihrer Länge bei einem Kartendienst. Die Länge der (zurückgelegten) Wegstrecke ist immer eine positive Zahl (Skalar).
Hast du für das Durchfahren einer Wegstrecke mit der Länge \(l\) die Zeit \(t\) benötigt, kannst du dir die Durchschnittsgeschwindigkeit \(\overline{v}\) (engl. average speed) ausrechnen:
| \[\begin{equation} \overline{v} = \frac{l}{t}=\frac{\text{Länge der Wegstrecke}}{\text{dafür benötigte Zeit}} \tag{3.1} \end{equation}\] |
So wie die Weglänge und die Zeitdauer ist dann auch die Durchschnittsgeschwindigkeit eine positive Zahl (Skalar). Die Durchschnittsgeschwindigkeit wird zum Beispiel bei Rennen angegeben oder von der Polizei bei einer Abschnittskontrolle (engl. section control) verwendet.
Der oben definierte Begriff der Durchschnittsgeschwindigkeit ist aber für die meisten physikalischen Fragestellungen zu ungenau:
Er enthält keine Richtungsinformation. Zum Beispiel ist es für ein Navi wichtig zu wissen, in welche Richtung sich das Fahrzeug bewegt.
Der Wert sagt nur relativ wenig über die tatsächliche Bewegung eines Körpers aus (siehe auch das Anwendungsbeispiel zur Durchschnittsgeschwindigkeit).
Aus diesen Gründen baut der Geschwindigkeitsbegriff in der Physik auf den Begriff der mittleren Geschwindigkeit auf, den du in einem der nächsten Abschnitte kennenlernen wirst.
3.2.2 Einheit der Geschwindigkeit
Weg hat die Einheit einer Länge. Die SI-Einheit der Länge ist das Meter (\(\mathrm{m}\)) und die der Zeit die Sekunde (\(\mathrm{s}\)). Setzt du in die Definitionsgleichung der Durchschnittsgeschwindigkeit diese Einheiten ein, erhältst du:
\[ [v] = \frac{[l]}{[t]} = 1\;\frac{\mathrm{m}}{\mathrm{s}} \]
Daraus ergibt sich als Einheit der Geschwindigkeit „Meter pro Sekunde“.
Im Alltag findest du oft die Einheit \(\mathrm{km}/\mathrm{h}\) („Kilometer pro Stunde“). Ein Kilometer sind 1000 Meter und eine Stunde enthält 3600 Sekunden (60 Minute mit jeweils 60 Sekunden). Für eine Geschwindigkeit von zum Beispiel \(36\;\mathrm{km}/\mathrm{h}\) erhältst du:
\[ 36\;\frac{\mathrm{km}}{\mathrm{h}} =36\cdot\frac{1000}{3600}\;\frac{\mathrm{m}}{\mathrm{s}} =36\cdot\frac{1}{3{,}6}\;\frac{\mathrm{m}}{\mathrm{s}} =10\;\frac{\mathrm{m}}{\mathrm{s}} \]
Um \(\mathrm{km}/\mathrm{h}\) in \(\mathrm{m}/\mathrm{s}\) umzurechnen, musst du also den Zahlenwert durch \(3{,}6\) dividieren. Bei der Umrechnung von \(\mathrm{m}/\mathrm{s}\) in \(\mathrm{km}/\mathrm{h}\) mit dem Faktor \(3{,}6\) multiplizieren (Bild 3.12).
Wenn du dir nicht merken kannst, ob du bei einer Umrechnung durch \(3{,}6\) oder mal \(3{,}6\) rechnen sollst, hilft dir vielleicht folgender Tipp: Der Zahlenwert der Geschwindigkeit ist bei der Einheit \(\mathrm{m}/\mathrm{s}\) immer kleiner als bei der Einheit \(\mathrm{km}/\mathrm{h}\).
3.2.3 Beispiele für Geschwindigkeitswerte
Um dir eine Vorstellung von der Größe der Geschwindigkeitseinheiten zu geben, findest du hier einige Werte aus der Praxis.
| Meter pro Sekunde | Kilometer pro Stunde | |
|---|---|---|
| Driftgeschwindigkeit zwischen Kontinentalplatten | \(0{,}000000001=10^{-9}\;\mathrm{m/s}\) | \(0{,}00000001=10^{-8}\;\mathrm{km/h}\) |
| Menschliches Haarwachstum | \(0{,}000000001=10^{-9}\;\mathrm{m/s}\) | \(0{,}00000001=10^{-8}\;\mathrm{km/h}\) |
| Meile pro Stunde (\(1=\;\mathrm{mph}\)) | \(0{,}44704\;\mathrm{m/s}\) | \(1{,}609344\;\mathrm{km/h}\) |
| Durchschnittliche Laufgeschwindigkeit | \(4{,}98\;\mathrm{m/s}\) | \(16{,}89\;\mathrm{km/h}\) |
| Schallgeschwindigkeit in Luft (bei Normalbedingungen) | \(340{,}3\;\mathrm{m/s}\) | \(1225\;\mathrm{km/h}\) |
| Orbitalgeschwindigkeit der Erde um die Sonne | \(29{.}800\;\mathrm{m/s}\) | \(107{.}280\;\mathrm{km/h}\) |
| Lichtgeschwindigkeit | \(2.9979246\cdot 10^{8}\approx3\cdot 10^{8}\;\mathrm{m/s}\) | \(1.0792528\cdot 10^{9}\approx1\cdot 10^{9}\;\mathrm{km/h}\) |
Links:
3.2.4 Anwendungsbeispiel: Durchschnittsgeschwindigkeit
Auf einem Autobahnstück der Länge \(10\;\mathrm{km}\) wird das Tempolimit von \(100\;\mathrm{km/h}\) mithilfe einer Abschnittskontrolle überwacht. Ein Auto fährt die erste Hälfte der Strecke nur mit der halben erlaubten Geschwindigkeit. Berechne die maximale Geschwindigkeit, mit der die zweite Hälfte durchfahren werden darf, ohne dass die Abschnittskontrolle einen Verstoß meldet (bei null Toleranz).
Berechnen wir zunächst die Zeit, die ein Auto, das mit der maximal erlaubten Geschwindigkeit von \(100\;\mathrm{km/h}\) fährt, für die Gesamtstrecke benötigt.
\[ \begin{aligned} v = {} & \frac{\ell}{t}&&\qquad\Bigr\rvert\cdot \frac{t}{v} \\ \cancel{v}\cdot \frac{t}{\cancel{v}} = {} & \frac{\ell}{\cancel{t}}\cdot \frac{\cancel{t}}{v} \\ t = {} & \frac{10\;\mathrm{km}}{100\;\mathrm{km/h}} \\ t = {} & 0.1\;\mathrm{h} \\ \end{aligned} \]
oder \(6\) Minuten. Bei jeder kürzeren Durchfahrtszeit meldet die Abschnittskontrolle einen Verstoß.
Fährt das Auto aber nur mit der halben Geschwindigkeit, befindet sich das Fahrzeug nach dieser Zeit gerade einmal bei der Hälfte der Strecke. Daraus folgt das erstaunliche Resultat, dass der Fahrer die zweite Hälfte mit beliebig großer Geschwindigkeit fahren kann, ohne dass die Abschnittskontrolle einen Verstoß meldet!
Intuitiv würdest du vielleicht als Antwort \(150\;\mathrm{km/h}\) geben, weil das arithmetische Mittel aus beiden Geschwindigkeiten genau das Tempolimit ergibt:
\[ \overline{v} = \frac{50+150}{2} = 100\;\mathrm{km/h} \]
Das arithmetische Mittel darf hier aber nicht verwendet werden, weil nicht berücksichtigt wird, dass das Fahrzeug mit der langsameren Geschwindigkeit viel länger unterwegs ist. Um die Durchschnittsgeschwindigkeit bei zwei gleich langen Streckenabschnitten zu berechnen, musst du das gewichtete harmonische Mittel verwenden.
3.2.5 Mittlere Geschwindigkeit
In der Physik ist die mittlere Geschwindigkeit \(\vec{v}_\text{m}\) (engl. average velocity) als Quotient aus Ortsänderung \(\Delta \vec{s}\) (engl. displacement) und Zeitänderung \(\Delta t\) definiert:
| \[\begin{equation} \vec{v}_m =\frac{ \vec{s}_2 - \vec{s}_1 }{t_2-t_1} =\frac{ \Delta\vec{s} }{\Delta t} =\frac{\text{Ortsänderung}}{\text{benötigte Zeit}} \tag{3.2} \end{equation}\] |
Dabei entspricht:
- \(\vec{s}_1\) dem Ort (Ortsvektor) eines Objektpunktes zum früheren Zeitpunkt \(t_1\) und
- \(\vec{s}_2\) dem Ort (Ortsvektor) desselben Objektpunktes zu einem späteren Zeitpunkt \(t_2\).
Die Angabe eines Orts in einem Koordinatensystem entspricht einem Vektor (Ortsvektor). Die Differenz von zwei Vektoren ergibt ebenfalls einen Vektor (Bild 3.13). Im Gegensatz dazu sind Zeitangaben Zahlen (Skalare) und die Differenz ebenfalls eine Zahl. Die Division eines Vektors durch eine Zahl ergibt einen Vektor, und somit ist die mittlere Geschwindigkeit eine Vektorgröße – sie hat eine Größe und eine Richtung (dieselbe Richtung wie die Ortsänderung).
Als Symbol für die Änderung eines Wertes wird in der Physik häufig der griechische Großbuchstabe Delta \(\Delta\) verwendet. Für die Änderung musst du immer „Wert nachher minus Wert vorher“ rechnen. Beachte: Das Delta ist kein zusätzlicher Faktor, sondern ein Symbol für die Differenz zweier Werte – es darf also nicht im Bruch gekürzt werden.
Bei \(\Delta t\) wird im Allgemeinen von einem kurzen Zeitintervall ausgegangen. Wählst du das Zeitintervall zu groß, liefert die mittlere Geschwindigkeit manchmal unbrauchbare Ergebnisse. Kommst du zum Beispiel nach einem Urlaub wieder nach Hause zurück, hast du vielleicht einen Weg von mehreren Hunderten Kilometern zurückgelegt. Der Ort vor und nach dem Urlaub ist aber identisch. Damit ist deine Ortsänderung und damit auch deine mittlere Geschwindigkeit über die Dauer des gesamten Urlaubs gleich null!
Übrigens: In der Definition der mittleren Geschwindigkeit kommt der Quotient aus zwei Differenzen vor. Ein solcher Ausdruck heißt Differenzenquotient und wird uns in diesem Buch noch öfters begegnen.
3.2.6 Anwendungsbeispiel: mittlerer Geschwindigkeit (1D)
Berechne für die Stroboskop-Aufnahmen a) bis c) die mittlere Geschwindigkeit (Bild 3.14).
In allen drei Stroboskop-Aufnahmen kannst du sehen, dass sich das Fahrzeug entlang einer Geraden (gerades Straßenstück) bewegt. In diesem einfachen Fall kann der Ort des Fahrzeugs durch eine Zahl (eigentlich einem eindimensionalen Vektor) beschrieben werden. Du siehst die Angabe der Orte über dem Fahrzeug als (gerichteter) Abstand vom Koordinaten-Ursprung aus eingezeichnet. Außerdem ist bei jeder Bewegungsphase der Zeitpunkt der Messung angegeben. Wir beginnen mit der Bewegung a) und setzen in Gleichung (3.2), der Definition der mittleren Geschwindigkeit, ein:
\[ v_m =\frac{ s_2 - s_1}{t_2 - t_1} =\frac{ 10\;\mathrm{m} - 4\;\mathrm{m}}{3\;\mathrm{s} - 1\;\mathrm{s}} = \frac{6\;\mathrm{m}}{2\;\mathrm{s}} = 3\;\mathrm{m/s} \]
Für die Stroboskop-Aufnahme b) erhalten wir:
\[ v_m =\frac{ s_2 - s_1}{t_2 - t_1} =\frac{ 2\;\mathrm{m} - (-4)\;\mathrm{m}}{3\;\mathrm{s} - 1\;\mathrm{s}} = \frac{6\;\mathrm{m}}{2\;\mathrm{s}} = 3\;\mathrm{m/s} \]
Beachte, dass wir in den Stroboskop-Aufnahmen a) und b) eigentlich dieselbe Bewegung sehen. Allerdings verwenden wir in beiden Fällen ein anderes Koordinatensystem. Die Werte für die Orte und Zeiten können zwar abweichen, die mittlere Geschwindigkeit für dasselbe Stroboskop-Bild – unabhängig vom gewählten Koordinatensystem – muss natürlich identisch sein. An dieser Aufgabe siehst du auch, wie wichtig es ist, alle Zeiten und Orte mit dem richtigen Vorzeichen einzusetzen. Nur so erhältst du das richtige Ergebnis für die mittlere Geschwindigkeit.
Für die Stroboskop-Aufnahme c) erhalten wir schließlich:
\[ v_m =\frac{ s_2 - s_1}{t_2 - t_1} =\frac{ -4\;\mathrm{m} - 2\;\mathrm{m}}{3\;\mathrm{s} - 1\;\mathrm{s}} = \frac{-6\;\mathrm{m}}{2\;\mathrm{s}} = -3\;\mathrm{m/s} \]
In diesem Fall ist die mittlere Geschwindigkeit negativ. Bei dem von uns gewählten Koordinatensystem bedeutet eine negative Geschwindigkeit, dass sich das Fahrzeug nach links bewegt; eine positive mittlere Geschwindigkeit bedeutet eine Bewegung nach rechts. Berücksichtigen wir die Orientierung des Fahrzeugs, können wir die negative Geschwindigkeit in diesem Fall als ein „Rückwärtsfahren“ interpretieren.
3.2.7 Anwendungsbeispiel: mittlerer Geschwindigkeit (2D)
Bei einem Slotcar-Rennen engl. slot car racing) wurde die Position des Modellautos im zeitlichen Abstand von jeweils \(\Delta t=0{,}1\;\mathrm{s}\) ermittelt und in dem Diagramm 3.15 eingezeichnet.
Wir berechnen die mittlere Geschwindigkeit zwischen zwei aufeinander folgenden Punkten der Aufzeichnung. Wir wählen zum Beispiel die Punkte \(P_{30}\) und \(P_{31}\). Der entsprechende Abschnitt aus der Datentabelle lautet:
| t | x(t) | y(t) | |
|---|---|---|---|
| 30 | 2.9 | 0.7038612 | 1.147370 |
| 31 | 3.0 | 0.1544050 | 1.632184 |
Zunächst benötigen wir den Vektor der Ortsänderung:
\[ \Delta\vec{s} = \vec{s}_{31} - \vec{s}_{30} = {\vec{sx}_{31} - \vec{sx}_{30} \choose \vec{sy}_{31} - \vec{sy}_{30}} = {0{,}15\ldots - 0{,}70\ldots \choose 1{,}63\ldots - 1{,}14\ldots} = {-0{,}54\ldots\;\mathrm{m} \choose 0{,}48\ldots\;\mathrm{m}} \]
Als Nächstes berechnen wir das Zeitintervall zwischen beiden Messpunkten:
\[ \Delta t = 3 - 2.9 = 0.1\;\mathrm{s} \]
Aus dem Quotienten aus Ortsänderung und Zeitänderung erhalten wir den Vektor der mittleren Geschwindigkeit:
\[ \vec{v}_m =\frac{ \Delta\vec{s} }{\Delta t} = {-0{,}54\ldots/0.1 \choose 0{,}48\ldots/0.1} = {-5{,}49\ldots\;\mathrm{m/s} \choose 4{,}84\ldots\;\mathrm{m/s}} \]
3.2.8 Momentangeschwindigkeit
Wählen wir immer kleinere Zeitintervalle für die Berechnung der mittleren Geschwindigkeit, können wir feststellen, dass sich der Wert immer weniger ändert. Auf diese Weise erhalten wir die Momentangeschwindigkeit \(\vec{v}\) (engl. instantaneous velocity) eines Punktes zu einem bestimmten Zeitpunkt.
Wählst du ein sehr kleines Zeitintervall, ist der Unterschied zwischen mittlere Geschwindigkeit und Momentangeschwindigkeit zahlenmäßig vernachlässigbar klein. Trotzdem sind beide sehr unterschiedliche Konzepte! Während die mittlere Geschwindigkeit immer eine Ortsänderung voraussetzt, ist die Momentangeschwindigkeit eine Eigenschaft, die ein Körper zu allen Zeitpunkten besitzt, auch wenn keine Zeit verstreicht. So wie du einem Körper auch die Farbeigenschaft „Blau“ zuordnen kannst, auch wenn gerade kein Licht im Raum vorhanden ist und seine Körperfarbe nicht erkennbar ist.
Einen exakten Wert für die Momentangeschwindigkeit lässt sich erst mithilfe des Grenzwertbegriffs der Infinitesimalrechnung berechnen. Er ist definiert als:
| \[\begin{equation} {\vec {v}} ={\underset {\Delta t\rightarrow 0}{\lim }}{\frac {\Delta {\vec {s}}}{\Delta t}} ={\frac {\mathrm {d} {\vec {s}}}{\mathrm {d} t}} \tag{3.3} \end{equation}\] |
In der Praxis gehen wir stets von sehr kleinen Zeitintervallen \(\Delta t\) aus und unterscheiden zwischen Momentangeschwindigkeit und mittlerer Geschwindigkeit nicht so genau und sprechen nur noch von Geschwindigkeit.
3.2.9 Tempo
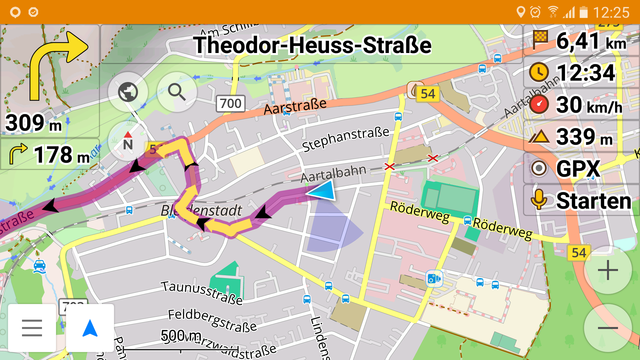
Streng genommen kann der Wert, der dir am Tachometer oder am Navi-Bildschirm (Bild 3.17) angezeigt wird, nicht die Geschwindigkeit des Fahrzeugs im physikalischen Sinn sein.
Geschwindigkeit ist immer eine Vektorgröße und hat eine Richtung. Die Zahl auf der Anzeige hingegen ist immer eine positive Zahl oder null. Sie entspricht der Länge (Betrag) des Geschwindigkeitsvektors. Hat ein Körper zum Beispiel eine Geschwindigkeit von
\[ \vec{v} = \binom{3\;\mathrm{m/s}}{-4\;\mathrm{m/s}}, \]
wird dir der Wert
\[ |\vec{v}| = \sqrt{3^2+(-4)^2}= 5\;\mathrm{m/s} \]
angezeigt. Diese (ungerichtete) Zahlengröße heißt – zur Unterscheidung der Vektorgröße Geschwindigkeit – Tempo (oder Schnelligkeit) (engl. speed). Der Begriff Tempo kommt im Alltag allerdings nur selten vor, gerade einmal in den Begriffen Tempolimit und Tempomat. Die meisten Menschen sprechen auch hier – nicht ganz korrekt – von „Geschwindigkeit“. Aus demselben Grund sollte auch die Durchschnittsgeschwindigkeit eigentlich als Durchschnittstempo bezeichnet werden.
