7.9 Anwendungen von rotierenden Bezugssystemen
Im letzten Kapitel haben wir den Begriff des rotierenden Bezugssystems kennengelernt und uns eingehend mit den darin auftretenden Scheinkräften, der Zentrifugalkraft, der Corioliskraft und der Eulerkraft, beschäftigt. Die Betrachtung einer Bewegung aus der Sicht eines rotierenden Bezugssystems ist in den meisten Fällen sehr kompliziert.
Wenn wir uns für ein rotierendes Bezugssystem entscheiden, dann wählen wir am besten eines, das relativ zu unserem beobachteten Körper ruht. In diesem speziellen Fall sind sowohl die Coriolis- als auch die Eulerkraft null. Und nur in diesem Spezialfall ist die Zentrifugalkraft entgegengesetzt gleich groß der Zentripetalkraft! Wenn ein Körper in einem Bezugssystem ruht, muss die Summe aller (Schein)kräfte null sein! Durch den Wechsel auf ein rotierendes Bezugssystem führen wir ein dynamisches Problem auf ein statisches zurück.
Neben neuen Beispielen (Bild 7.84) greifen wir in den folgenden Abschnitten auch einige Beispiele auf, die wir schon früher in einem Inertialsystem betrachtet haben, und erklären sie aus der Sicht eines speziell gewählten rotierenden Bezugssystems. Die Beschreibung ist jetzt anders, die Physik dahinter bleibt natürlich dieselbe. Für welches Bezugssystem du dich letzten Endes bei einer konkreten Aufgabe entscheidest, ist oft Geschmacksache. Es gibt kein falsches oder richtiges Bezugssystem, nur sind einige in der jeweiligen Situation vielleicht praktischer als andere.
7.9.1 Kreispendel im rotierenden Bezugssystem
Die Kräfte bei einem Kreispendel aus der Sicht eines Inertialsystems haben wir uns bei der Anwendung des Kettenkarussells angesehen. In einem rotierenden Bezugssystem, in dem der Pendelkörper ruht, fallen die Drehachsen von Bezugssystem und Karussell zusammen und die Winkelgeschwindigkeit von beiden ist gleich groß. In diesem Bezugssystem stellen sich die Kräfte wie in Bild 7.85 dar.
In diesem Bezugssystem gibt es keine Beschleunigung, daher fällt die Zentripetalkraft weg. Dafür muss die in allen rotierenden Bezugssystemen auftretende Zentrifugalkraft berücksichtigt werden. In einem statischen Problem ist die Gesamtkraft null, daher gilt:
\[ \vec{T} + \vec{F}_\text{G} + \vec{F}_\text{Zf} = 0 \]
Und für die Seilkraftkomponenten gilt dann:
\[ \begin{aligned} \vec{T}_x = {} & - \vec{F}_\text{Zf} \\ \vec{T}_y = {} & - \vec{F}_\text{G} \\ \end{aligned} \]
7.9.2 Looping im rotierenden Bezugssystem
Die Kräfte bei einem Looping aus der Sicht eines Inertialsystems haben wir uns bei dem Anwendungsbeispiel der Achterbahn angesehen. Dort haben wir festgestellt, dass der entscheidende Zeitpunkt der höchste Punkt im Looping ist. Wählen wir zu diesem Zeitpunkt ein Bezugssystem, in dem der Wagen ruht, stellen sich die Kräfte wie in Bild 7.86 dar.
Im gewählten Bezugssystem tritt keine Beschleunigung auf, daher fällt die Zentripetalkraft weg. Dafür muss die in allen rotierenden Bezugssystemen auftretende Zentrifugalkraft berücksichtigt werden. Damit der Wagen auch am höchsten Punkt noch Kontakt zu den Schienen hat, darf dort die Zentrifugalkraft nicht kleiner als die Gewichtskraft werden. Aus der Kräftesumme
\[ \vec{F}_\text{G} + \vec{F}_\text{Zf} = 0 \]
folgt:
\[ \vec{F}_\text{Zf} = -\vec{F}_\text{G} \]
7.9.3 Kurvenfahrt mit einem Zweirad
Im Gegensatz zu Autos benötigen einspurige Fahrzeuge immer eine Schräglage, um stabil in einer Kurve zu fahren. Für die Untersuchung der Kurvenfahrt mit einem Zweirad verwenden wir ein rotierendes Bezugssystem, das wir exakt so wählen, dass du und dein Bike in diesem ruhen.
Vereinfacht betrachten wir dich und dein Bike als einen einzigen starren Körper 7.87. An dessen Massenmittelpunkt greifen die Gewichtskraft und die Zentrifugalkraft an. Mit dem Kontaktpunkt am Boden erzeugt die Zentrifugalkraft ein aufrichtendes Drehmoment und die Gewichtskraft ein Drehmoment in die andere Richtung. Damit du in der Kurve nicht umkippst, müssen sich beide Drehmomente gerade aufheben.
\[ -M_\text{G} = M_\text{Zf} \]
Nachdem der Radiusvektor \(r\) für beide Drehmomente gleich groß ist, müssen sich die Tangentialkomponenten beider Kräfte die Waage halten:
\[ \begin{aligned} - F_\text{G} \cdot \sin(\alpha)= {} & F_\text{Zf} \cdot \cos(\alpha)\\ m \cdot g \cdot \sin(\alpha) = {} & \frac{m\cdot v^2}{r} \cdot \cos(\alpha) &&\qquad\Bigr\rvert\cdot \frac{1}{\cos(\alpha)\cdot g\cdot m}\\ \frac{\sin(\alpha)}{\cos(\alpha)} = {} & \frac{ v^2}{r \cdot g} \\ \tan(\alpha) = {} & \frac{v^2}{r \cdot g} \\ \alpha = {} & \tan^{-1}\left(\frac{v^2}{r \cdot g}\right) \\ \end{aligned} \]
Der Neigungswinkel \(\alpha\) bei der Kurvenfahrt hängt also nur von der Bahngeschwindigkeit \(v\), dem Kurvenradius \(r\) und der Fallbeschleunigung \(g\) ab – ist also unabhängig von deiner Masse und der deines Bikes. Ab einer gewissen Neigung würden Teile des Zweirads am Boden streifen. Um den Neigungswinkel noch weiter zu erhöhen, gibt es keine andere Möglichkeit, als sich seitlich von der Maschine in Richtung Kurvenmittelpunkt zu hängen und so den gemeinsamen Schwerpunkt noch weiter abzusenken (Bild 7.84).
Damit du nicht seitlich wegrutschst, muss zusätzlich zu den Drehmomenten auch noch die Summe aller Kräfte null sein und da kommt jetzt die Reibungskraft ins Spiel.
\[ F_\text{R} = \mu_\text{H}\cdot F_\text{N} \]
Dabei ist \(\mu_\text{H}\) die Haftreibungszahl. Setzen wir für diese Kräfte ihre jeweils gleich großen Gegenkräfte \(F_\text{Zf}\) und \(F_\text{G}\) ein, erhalten wir den Ausdruck:
\[ \begin{aligned} F_\text{Zf} = {} & \mu_\text{H}\cdot F_\text{G} \\ \frac{m\cdot v^2}{r} = {} & \mu_\text{H}\cdot m\cdot g &&\qquad\Bigr\rvert\cdot \frac{1}{m\cdot g}\\ \frac{v^2}{r\cdot g} = {} & \mu_\text{H}\\ \end{aligned} \]
Solange der Ausdruck auf der linken Seite kleiner als die Haftreibungszahl ist, rutscht das Bike in der Kurve nicht von der Fahrbahn. Interessanterweise spielt auch hier die Masse wieder keine Rolle. Durch Einsetzen folgt für den maximalen Neigungswinkel:
\[ \alpha_\text{max} = \tan^{-1}\left( \mu_\text{H}\right) \]
Gehen wir vom günstigen Fall einer trockenen Straße und einer Haftreibungszahl von rund \(0{,}65\), erhalten wir als maximalen Neigungswinkel \(\alpha_\text{max} = 33{,}02\ldots\).
Noch ein Nachsatz: Nach dem hier vorgestellten einfachen Modell wäre die Kurvenfahrt auf einem Zweirad eine nahezu unmögliche Aufgabe. Jede kleinste Abweichung vom Gleichgewichtsneigungswinkel würde durch das jeweils überwiegende Drehmoment sofort verstärkt werden – ein sofortiger Sturz wäre die Folge. Eine tatsächliche Kurvenfahrt mit einem Zweirad ist dagegen relativ tolerant – jeder von uns schafft es mit ein wenig Übung. Warum Fahrräder diese Eigenstabilität besitzen, ist bisher nicht restlos geklärt. Oder wie Michael Brooks es ausdrückte: „Vergessen wir die mysteriöse dunkle Materie und dunkle Energie; das Fahrrad stellt eine weitaus peinlichere Lücke in den Errungenschaften der Physik dar.“
Links:
7.9.4 Lagrange-Punkte im rotierenden Bezugssystem
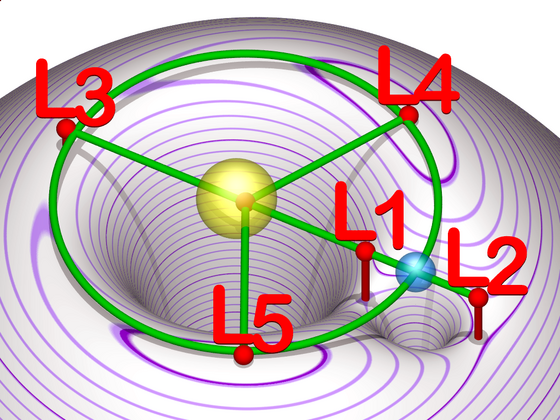
In einem früheren Kapitel haben wir bereits die Lagrange-Punkte besprochen. Betrachten wir die Situation aus dem Blickwinkel eines rotierenden Bezugssystems. Als Drehmittelpunkt für unser Bezugssystem wählen wir das Baryzentrum von Erde und Sonne. Die Drehgeschwindigkeit wählen wir genau so, dass Erde und Sonne in unserem rotierenden Bezugssystem ruhen, dann erscheinen auch die Lagrange-Punkte unbewegt (Bild 7.89).
Durch unsere Wahl des Bezugssystems, in dem alle relevanten Punkte ruhen, haben wir wieder eine statische Situation herbeigeführt. Daher muss für jeden Lagrange-Punkt die Kräftesumme null sein. Da es (relativ zum Bezugssystem) keine Bewegung gibt, braucht es auch keine Zentripetalkraft. Stattdessen müssen wir die im rotierenden Bezugssystem auftretende Zentrifugalkraft berücksichtigen. In Bild 7.90 siehst du das Potenzialgelände für das mitrotierenden Bezugssystem, welches durch Gravitations- und Zentrifugalkräfte erzeugt wird.
Obwohl sich die Punkte \(L_4\) und \(L_5\) auf der Spitze eines Potenzialhügels befinden, sind diese Punkte im Gegensatz zu den drei anderen Lagrange-Punkten trotzdem stabil. Der Grund dafür ist die geschwindigkeitsabhängige Corioliskraft, die in der Darstellung eines Potenzialgefälles nicht gezeigt werden kann. Wenn sich ein Körper von der exakten Lagrange-Position entfernt, sorgt die Coriolis-Beschleunigung für eine Umlaufbahn um diesen Langrange-Punkt. Asteroide oder Monde, die die Punkte \(L_4\) und \(L_5\) umkreisen, werden in der Astronomie als Trojaner bezeichnet. Am Punkt \(L_4\) im System Erde-Sonne befindet sich zum Beispiel der Asteroid 2010 TK₇. Das System Sonne-Jupiter hat sogar mehr als eine Million solcher Trojaner!