4.7.1 Mathematische Beschreibung der Reibungskraft zwischen Festkörpern

Alle Reibungskräfte zwischen Festkörpern (engl. dry friction) werden durch die dieselbe Formel beschrieben:

In dieser Formel bedeutet:

• \(F_{\mathrm{R}}\) die Reibungskraft (in \(\mathrm{N}\))
• \(F_{\mathrm{n}}\) die Anpresskraft normal auf die Oberfläche (in \(\mathrm{N}\))
• \(\mu\) der Reibungskoeffizient oder Reibungszahl (engl. coefficient of friction) (dimensionslose Zahl)

Bild 4.52: Richtungen von Normalkraft und Reibungskraft

Diese Reibungszahlen müssen für unterschiedliche Oberflächen experimentell ermittelt werden und können in Tabellen nachgeschlagen werden. Bei dem Reibungskoeffizienten oder der Reibungszahl handelt es sich um ein Verhältnis von zwei Kräften. Daher ist die Reibungszahl eine dimensionslose Größe – einfach eine Zahl. Je nach Reibungsart muss in die Formel ein anderer Reibungskoeffizient verwendet werden:

• Für die Haftreibungskraft die entsprechende Haftreibungszahl,
• für die Gleitreibungskraft die entsprechende Gleitreibungszahl und
• für die Rollreibungskraft die entsprechende Rollreibungszahl.

Hier noch einige Bemerkungen zu dieser Formel:

• Vielleicht ist dir aufgefallen, dass in dieser Gleichung keine Vektorpfeile über den Kräften stehen. Diese Gleichung sagt daher nur etwas über die Größe (Länge) der Kraftpfeile aus, aber nichts über ihre Richtungen.

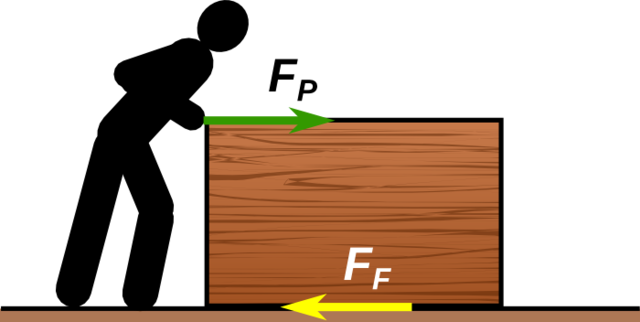
• Die Reibungskraft behindert stets die Bewegung. Daher verläuft die Reibungskraft hier immer parallel zur Oberfläche, auf dem sich der Körper bewegt und zeigt in die Gegenrichtung der Bewegung (Bild 4.52).

• Die Reibungskraft zwischen Festkörpern ist unabhängig von der Größe der Kontaktfläche. Intuitiv würdest du vielleicht vermuten, dass die Reibungskraft mit zunehmender Kontaktfläche größer werden müsste. Bei einer größeren Fläche verteilt sich aber die Anpresskraft auf eine größere Fläche, sodass der Druck im selben Verhältnis sinkt (2. Amontonssche Gesetz engl. Amontons’ Second Law). Für weiche Gummireifen gilt diese Näherung zum Beispiel nicht mehr – hier erhöht sich die Reibung mit der Fläche.

• In der Formel kommt die Geschwindigkeit nicht vor. Die Reibungskraft zwischen Festkörpern ist unabhängig von der Geschwindigkeit (engl. Coulomb’s Law of Friction). Bei großen Geschwindigkeiten muss die zusätzlich auftretende geschwindigkeitsabhängige Luftwiderstandskraft berücksichtigt werden.

4.7.2 Haftreibungskraft

Von Haftreibungskraft (engl. static friction) wird gesprochen, wenn sich ein Körper noch nicht in Bewegung befindet. Versuchst du einen schweren Gegenstand über den Boden zu schieben, benötigst du eine gewisse Kraft, um überhaupt eine Bewegung des Gegenstandes zu erreichen.

Bild 4.53: Kräftegleichgewicht: Druckkraft und gleich große entgegengesetzte Haftreibungskraft

Übst du Kraft auf einen Gegenstand aus, müsste dieser sich nach dem dynamischen Grundgesetz beschleunigt bewegen. Bewegt sich der Körper aber nicht, muss es eine gleich große Gegenkraft geben, die das verhindert – die Summe muss stets null sein (Bild 4.53). Die Haftreibungskraft ist also keine konstante Kraft, sondern wächst mit der Kraft, mit der du drückst. Mit der Reibungsformel kannst du die Kraft berechnen, die notwendig ist, um einen Körper (auf einem bestimmten Untergrund) überhaupt in Bewegung zu versetzen. Wir sollten daher besser von der maximalen Haftreibungskraft sprechen.

Zum Beispiel soll ein \(5\;\textrm{kg}\) Stein auf einem ebenen Holzboden geschoben werden. Für die Haftreibungszahl der Oberflächenkombination Stein auf Holz findest du in der Literatur den Wert \(\mu_{H} = 0{,}9\). Auf einem ebenen Untergrund entspricht die Anpress- oder Normalkraft gerade der Gewichtskraft des Körpers. Mit einer Fallbeschleunigung von \(g=9{,}81\;\mathrm{m}/\mathrm{s}^2\) erhalten wir eine Normalkraft von \(F_{\mathrm{N}}=49{,}05\;\mathrm{N}\). In die Reibungsformel eingesetzt erhalten wir eine Haftreibungskraft von \(F_{\mathrm{R}} = 44{,}145\;\mathrm{N}\). Der Stein muss daher mit einer Kraft größer \(44{,}145\;\mathrm{N}\) angeschoben werden, damit er sich überhaupt in Bewegung setzt.

Bild 4.54: Messung der Kräfte beim Ziehen eines Körpers

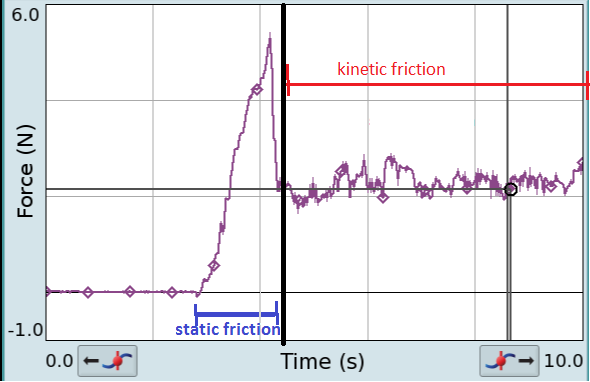
In der Abbildung 4.54 siehst du die Messung der Kräfte beim Ziehen eines Körpers auf einer festen Oberfläche. Du kannst im Diagramm erkennen, wie die Haftreibungskraft kontinuierlich mit der Zugkraft an dem Körper steigt, bis sie einen maximalen Wert erreicht und dann in die Gleitreibung übergeht.

4.7.3 Gleitreibungskraft

Auch wenn die Haftreibungskraft überwunden wird und sich der Körper jetzt bewegt, wird die Bewegung weiterhin durch eine Reibungskraft behindert – die Gleitreibungskraft (engl. sliding friction oder kinetic friction). Wie du im Diagramm 4.54 oben erkennen kannst, ist diese Reibungskraft kleiner als die maximale Haftreibungskraft und sie bleibt konstant – unabhängig von Geschwindigkeit und Zugkraft.

Verwendest du die Reibungsformel mit der Gleitreibungszahl, kannst du berechnen, um wie viel sich die Beschleunigung aufgrund der Oberflächenbeschaffenheiten verringert, wenn ein Körper über eine Oberfläche gleitet.

Zum Beispiel wird ein \(5\;\textrm{kg}\) Stein auf einem ebenen Holzboden mit \(F=100\;\mathrm{N}\) gezogen. Für die Gleitreibungszahl der Oberflächenkombination Stein auf Holz findest du in entsprechenden Tabellen den Wert \(\mu_{G} = 0{,}7\). Auf einem ebenen Untergrund entspricht die Anpress- oder Normalkraft gerade der Gewichtskraft des Körpers. Mit einer Fallbeschleunigung von \(g=9{,}81\;\mathrm{m}/\mathrm{s}^2\) erhalten wir eine Normalkraft von \(F_{\mathrm{N}}=49{,}05\;\mathrm{N}\). In die Reibungsformel eingesetzt erhalten wir eine Haftreibungskraft von \(F_{\mathrm{R}} = 34{,}335\;\mathrm{N}\). Um diesen Wert ist die Zugkraft vermindert, daher verbleibt für die Bewegung die Kraft \(F_{\mathrm{R}} = 100-34{,}335 = 65{,}665\;\mathrm{N}\). Die Beschleunigung ist daher nur \(g=65{,}665/5=13{,}133\;\mathrm{m}/\mathrm{s}^2\) (statt \(g=100/5=20\;\mathrm{m}/\mathrm{s}^2\)).

4.7.4 Rollreibungskraft

Aus Erfahrung wirst du auch wissen, dass es wesentlich leichter ist, ein Möbelstück mit Möbelrollen zu bewegen, als es über den Boden zu schieben. Die Rollreibungskraft (engl. rolling resistance) ist immer kleiner als die Gleitreibungskraft. Daher muss die Rollreibungszahl auch kleiner als die Haft- und Gleitreibungszahl sein.

Bei der Rollreibung ist keine größere anfängliche Kraft zu überwinden, damit ein Körper überhaupt anfängt, sich zu bewegen (im Gegensatz zum Gleiten). Egal ob aus dem Stand oder während der Bewegung – die Rollreibungskraft ist immer gleich groß.

Bild 4.55: Roll- und Kugellager

Bei Kugellagern (Bild 4.55) wird der Vorteil der Rollreibung gegenüber der Gleitreibung technisch genutzt. Solche Lager findest du zum Beispiel in den Rollen deines Skateboards und deiner Rollschuhe oder auch im Tretlager und der Radnabe deines Fahrrades.

4.7.5 Ursachen von Haft-, Gleit- und Rollreibung

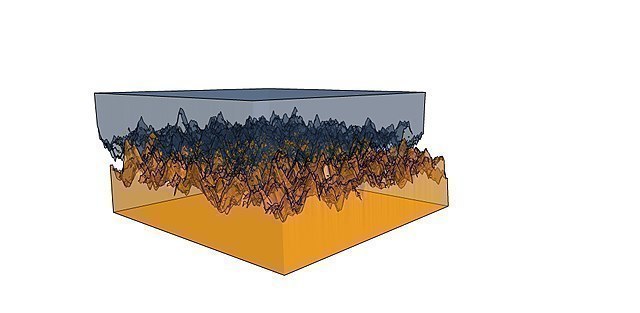
Aus Erfahrung weißt du vermutlich, dass die Reibung zwischen zwei Oberflächen geringer ist, wenn die Oberflächen glatter sind. Aber warum gibt es bei glatten Oberflächen immer noch Reibung? Um das zu sehen, müssen wir glatte Oberflächen unter dem Mikroskop betrachten (Bild 4.56).

Bild 4.56: Glatte Oberflächen unter dem Mikroskop

Wie du sehen kannst, sind selbst die makroskopisch glattesten Oberflächen mikroskopisch immer noch Gebirgslandschaften. Diese Unebenheiten verzahnen sich wie zwei Bürsten. Das ist der Grund, warum es selbst bei glatten Oberflächen immer noch Reibung gibt.

Warum ist die Gleitreibung kleiner als die Haftreibungskraft? Das mag verblüffen, da sich die Oberflächen durch die Gleitbewegung ja nicht ändern. Um einen Körper überhaupt schieben zu können, müssen sich zunächst der Körper so weit heben, dass die Zacken aneinander vorbeigleiten können. Wird ein Körper verschoben, fällt er zwar wieder ein wenig in die Täler und muss gehoben werden, aber nie wieder so tief wie zu Anfang, als er noch ruhte.

Und warum gibt es überhaupt eine Rollreibung? Wenn zwei glatte Oberflächen aufeinander abrollen, sollte es doch gar keine Reibung geben? Einerseits gibt es auch bei harten Rädern (zum Beispiel Stahlräder von Zügen auf Eisenbahnschienen) stets eine gewisse Verformung beim Abrollen. Für diese Walkbewegung ist Kraft erforderlich. Fährst du mit einem wenig aufgepumpten Fahrradreifen, wird dieser stärker durchgewalkt als ein prall aufgepumpter Reifen. Es ist mühsamer damit zu fahren und er wird schneller warm.