6.3 Newtons Gravitationsgesetz
Sowohl das durch Ptolemäus verbesserte geozentrische Modell als auch das durch Kepler verbesserte heliozentrische Modell haben die Bewegung von Himmelskörper erfolgreich beschrieben. Es scheint fast so, als wäre es reine Geschmackssache, welches der beiden Modelle für die Berechnung genommen wird.
Die Bahnen der Planeten waren bekannt, aber es fehlt noch das Verständnis, warum sie sich so bewegen. Das änderte sich durch die Entdeckung des Gravitationsgesetzes durch Isaac Newton.
6.3.1 Entdeckung des Gravitationsgesetzes
Vermutlich hast du die folgende Geschichte schon einmal gehört. Isaac Newton soll unter einem Apfelbaum eingeschlafen sein. Als er in der Nacht von einem herunter fallenden Apfel getroffen wird und aufwacht, erblickt er den Mond. In diesem Moment wird ihm klar: Sowohl der Apfel als auch der Mond folgen denselben physikalischen Gesetzen. Das soll in der Folge zur Formulierung des Gravitationsgesetzes geführt haben.
Auch wenn diese Geschichte mit sehr großer Wahrscheinlichkeit erfunden ist, verdeutlicht sie einen wesentlichen Punkt: Vor der Kopernikanischen Wende war die vorherrschende Meinung, dass das Geschehen im Himmel und auf der Erde unterschiedlichen Gesetzmäßigkeiten folge. Erst durch das (universelle) Gravitationsgesetz erfolgt eine Gleichstellung von irdischen und kosmischen Kräften – für alle Körper im Universum gelten dieselben physikalischen Gesetze (Kosmologisches Prinzip).
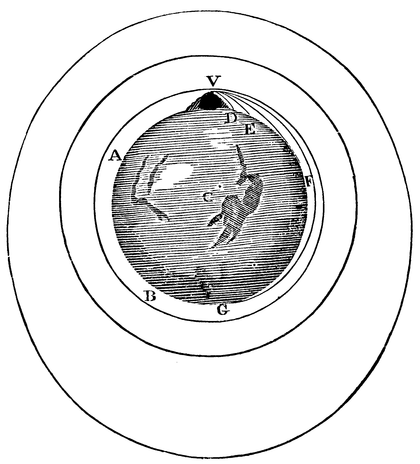
Wenn ein Apfel von der Erde angezogen wird, wird vielleicht auch der Mond von der Erde angezogen. Wenn ich einen Apfel waagrecht zur Erdoberfläche abschieße, fällt er nach ein paar Metern zu Boden. Je schneller ich den Apfel abschieße, desto weiter kommt er. Jetzt ist die Erde aber annähend eine Kugel. Könnte ich den Apfel so schnell abzuschießen, dass sein Herabfallen durch das Wegkrümmen der Erdoberfläche ausgeglichen wird, würde der Apfel immer auf derselben Höhe bleiben und ständig um die Erde „herumfallen“ (Bild 6.20). Natürlich nur unter der Voraussetzung, dass er nicht durch die Luftreibung oder andere Gegenstände auf seiner Bahn behindert wird. Der Apfel befände sich dann auf einer Umlaufbahn um die Erde – genauso wie der Mond (Bild 6.20).
6.3.2 Gravitationsgesetz
Alle Körper ziehen einander an. Diese Kraft zwischen jeweils zwei Körpern beschreibt das Newtonsches Gravitationsgesetz (engl. Newton’s law of universal gravitation):
| \[\begin{equation} F_\text{G}=G\cdot\frac{m_1\cdot m_2}{r^2} \tag{6.2} \end{equation}\] |
In dieser Formel bedeuten:
- \(F_G\), die Schwerkraft (Gravitation) zwischen zwei Körpern (in \(\mathrm{N}\))
- \(m_1\) und \(m_2\), die Massen der beiden Körper (in \(\mathrm{kg}\))
- \(G\), die Gravitationskonstante (in \(\mathrm{\frac {m^{3}}{kg\cdot s^{2}}}\))
- \(r\), der Abstand der Massenmittelpunkte (in \(\mathrm{s}\), Bild 6.21)
Die Gravitation zwischen zwei Körpern wirkt immer anziehend!
Streng genommen gilt das Gravitationsgesetz nur für punktförmige Massen. In Aufgaben, bei denen die Abstände zwischen den Körpern groß im Verhältnis zur Ausdehnung der Körper ist, kannst du so tun, also ob die gesamte Masse des Körpers in seinem Massenmittelpunkt konzentriert ist. In einigen Fällen wie der Berechnung der Gezeitenkräfte muss die räumliche Ausdehnung des Körpers berücksichtigt werden!
Links:
- Applet: Gravitationskraft
6.3.3 Gravitationsgesetz in Vektorschreibweise
Die Vektorform des Gravitationsgesetzes lautet:
\[\begin{equation} \vec{F}_{12}=-G\cdot\frac{m_1\cdot m_2}{|\vec{r}_{12}|^2}\cdot\frac{\vec{r}_{12}}{|\vec{r}_{12}|} \tag{6.3} \end{equation}\]
Dabei ist \(\vec{F}_{12}\) die Kraft, welche die Masse \(m_1\) auf die Masse \(m_2\) ausübt und \(\vec{r}_{12}\) der Verbindungsvektor von der Masse \(m_1\) zu der Masse \(m_2\) (Bild 6.22). Beachte das Minus in der Formel! Es besagt, dass sich der Abstand verkürzt, die Kraft also anziehend ist.
Die Formel mag dir auf den ersten Blick sehr kompliziert vorkommen. Wenn du dir aber überlegst, dass der Betrag eines Vektors nicht anderes als seine Länge ist, kannst du erkennen, dass der erste Teil der Formel dieselbe Zahl ist. Es handelt sich dabei um dieselbe Zahl, die du bereits aus der nicht-verktoriellen Formel des Gravitationsgesetzes kennst – sie ist einfach die Länge des Kraftvektors \(\vec{F}_{12}\).
Der letzte Faktor ist der Verbindungsvektor dividiert durch seine Länge, also der Einheitsvektor (der Richtungsvektor \(\vec{r}_{12}\) auf die Länge eins normiert) – er gibt lediglich die Richtung des Kraftvektors \(\vec{F}_{12}\) an.
Verwendest du die Vektorform des Gravitationsgesetzes, musst du dir die Richtung der Kraft nicht überlegen, sie ist bereits im Kraftvektor enthalten.
6.3.4 Gravitationskonstante
Der Faktor \(G\) im Gravitationsgesetz wird Gravitationskonstante (engl. gravitational constant) genannt. Soweit wir heute wissen, handelt es sich dabei um eine Naturkonstante, die im gesamten Universum den gleichen Wert besitzt.
Nach der Veröffentlichung des Gravitationsgesetzes durch Isaac Newton hat es noch mehr als 100 Jahre gedauert, bis Henry Cavendish um 1800 mit einer Drehwaage einen Wert für die Gravitationskonstante erstmalig bestimmen konnte. Ihr Wert beträgt:
\[ G = 6{,}67\cdot 10^{-11}\,\mathrm{\frac {m^{3}}{kg\cdot s^{2}}} \]
Mit Sicherheit ist dir das Minus im Exponenten der Gravitationskonstante aufgefallen. \(10^{-11}\) ist eine unglaublich kleine Zahl und damit ist die Gravitationskraft eine sehr, sehr kleine Kraft, die sich nur bei extrem großen Massen bemerkbar macht.
Die Einheit der Gravitationskonstante leitet sich direkt aus dem Gravitationsgesetz her.
\[ [G]= [F]\cdot\frac{[r]^2}{[m_1]\cdot[m_2]} = \textrm{N}\cdot\frac{\textrm{m}^2}{\textrm{kg}\cdot\textrm{kg}} = \frac{\textrm{kg}\cdot\textrm{m}}{\textrm{s}^2}\frac{\textrm{m}^2}{\textrm{kg}\cdot\textrm{kg}} = \mathrm {\frac {m^{3}}{kg\cdot s^{2}}} \]
6.3.5 1/r²-Gesetz (Abstandsgesetz)
Die Gravitationskraft nimmt mit dem Quadrat des Abstandes ab. Bei doppeltem Abstand sinkt die Kraft auf \(1/4\), bei dreifachem Abstand auf \(1/9\), und so weiter. Dieses Abstandsgesetz (engl. inverse-square law) ist keine Selbstverständlichkeit. Warum ist die Potenz nicht \(1{,}9\) oder \(2{,}1\)? Es wurden viele Experimente gemacht. Sie alle haben – im Rahmen ihrer Messgenauigkeit – gezeigt, dass der Exponent tatsächlich \(2\) ist.
Am besten kannst du dir das Abstandsgesetz über eine geometrische Vorstellung merken. Die Oberfläche einer Kugel ist durch die Formel
\[\begin{equation} A\,=4\pi r^2 \tag{6.4} \end{equation}\]
gegeben. Wenn du einen kugelförmigen Luftballon auf die doppelte Größe aufbläst, vervierfacht sich die Oberfläche. Bläst du ihn auf den dreifachen Radius auf, wächst die Oberfläche auf das neunfache (Bild 6.23). Du kannst dir vorstellen, dass sich die Gravitationskraft proportional zur Kugeloberfläche „verdünnt“ und damit schwächer wird.
6.3.6 Gravitationskraft bei mehr als zwei Massen
Mithilfe des Gravitationsgesetzes kannst du nur die Kraft zwischen zwei (punktförmigen) Massen ausrechnen. Willst du die Kraft auf eine Masse in einem System mit mehr als zwei Massen berechnen, musst du das Gravitationsgesetz wiederholt für jedes Massenpaar anwenden. Die Gesamtkraft auf diese Masse ergibt sich aus der Vektorsumme der Einzelkräfte.
In Bild 6.24 siehst du ein System aus drei Massen. Willst du die Gesamtkraft auf die Masse \(m_3\) berechnen, musst du die Vektorsumme aus den Kräften \(\vec{F}_{13}\) (Kraft der Masse 1 auf Masse 3) und \(\vec{F}_{23}\) (Kraft der Masse 2 auf Masse 3) bilden.
6.3.7 Träge und schwere Masse
Den Begriff „Masse“ ist uns bisher in zwei unterschiedlichen Funktionen begegnet.
Die träge Masse (engl. inertial mass) kommt im dynamischen Grundgesetz vor. Sie ist ein Maß dafür, wie stark sich ein Körper einer Beschleunigung widersetzt.
Die schwere Masse (engl. gravitational mass) kommt im Gravitationsgesetz vor. Sie ist die Quelle der Gravitationskraft und ein Maß dafür, wie stark Körper einander anziehen.
In der Geschichte der Physik hat es viele Versuche gegeben, einen Unterschied zwischen träger und schwerer Masse zu finden. Einige der genauesten Untersuchungen wurden um 1900 von Loránd Eötvös vorgenommen. Auch er fand – im Rahmen der Messgenauigkeit der Instrumente – keinen Unterschied.
Setzen wir die Gravitationskraft und die Gewichtskraft für einen Körper der Masse \(m\) gleich
\[ G\cdot\frac{M\cdot m}{r^2} = m\cdot g \]
können wir aufgrund der Gleichheit von träger und schwerer Masse die Gleichung durch \(m\) dividieren und erhalten:
\[\begin{equation} g = G\cdot\frac{M}{r^2} \tag{6.5} \end{equation}\]
Die Fallbeschleunigung ist also unabhängig von der Masse eines konkreten Körpers und hängt nur von Ort \(r\) und der Masse \(M\) des Planeten ab. Obwohl Körper mit größerer Masse eine größere Gravitationskraft erfahren, nimmt ihre Trägheit im selben Maß zu, sodass alle Körper am selben Ort prinzipiell gleich fallen (Bild 6.25).
Weil der Luftwiderstand auf der Erde den Fall von Gegenständen verzögert, hat die Mannschaft der Apollo 15 Mission am Mond bei einem Fallversuch mit einem Hammer und einer Feder das Äquivalenzprinzip gezeigt (Video 6.26).
Bild 6.26: Apollo 15 Fallexperiment auf dem Mond
Für seine Allgemeine Relativitätstheorie setzte Albert Einstein die Gleichheit von träger und schwerer Masse als Grundannahme voraus (Äquivalenzprinzips) und entwickelte daraus ein vollständig neues Modell der Gravitation.
Links:
6.3.8 Entdeckung des Neptun
Astronomen haben Mitte des 19. Jahrhunderts festgestellt, dass die Bahn des Planeten Uranus von den Vorhersagen des Newtonschen Gravitationsgesetzes abweicht. Urbain Le Verrier vermutete, dass die Bahnstörungen des Uranus auf einen bislang nicht entdeckten Planeten zurückzuführen sind. Mithilfe des Gravitationsgesetzes berechnete er die voraussichtliche Position am Himmel. Und tatsächlich fanden die Astronomen an der vorausberechneten Stelle einen neuen Planeten – den Planeten Neptun (Bild 6.27).
Eine andere, minimale Bahnabweichung – die sogenannte Periheldrehung des Merkurs – konnte aber bis zuletzt nicht mit dem Newtonschen Gravitationsgesetz erklärt werden. Dieses Rätsel konnte erst rund 50 Jahre später gelöst werden, als ein noch genaueres Modell der Gravitation entwickelt wurde – die allgemeine Relativitätstheorie.
