16.9 Gekrümmte Raumzeit
In Bild 16.89 siehst du die künstlerische Darstellung eines sogenannten „Wurmlochs“.
„Wurmlöcher“ sind ein beliebtes Thema in der Science-Fiction. Dort werden sie oft zur Reise im Weltraum verwendet, wie zum Beispiel im Film Interstellar, bei dem der Physiknobelpreisträger Kip Thorne als wissenschaftlicher Berater tätig war.
Im Kapitel Minkowski-Diagramme hast du bereits die ebene Raumzeit kennengelernt. Nachdem wir uns in diesem Kapitel zunächst mit Maßstäben im Gravitationsfeld beschäftigen, kommen wir zur gekrümmten Raumzeit. Wir werden uns mit den Ursachen und den Wirkungen der Raumkrümmung beschäftigen, ein neues Modell der Gravitation kennenlernen und uns unter anderem auch mit dem Phänomen des „Wurmlochs“ beschäftigen.
16.9.1 Maßstäbe im Gravitationsfeld
Stell dir vor, du befindest dich in einem Weltraum-Labor in einer elliptischen Umlaufbahn um die Erde (Bild 16.90).
Obwohl du auf deiner Umlaufbahn einmal näher und einmal weiter von der Erde bist, herrscht zu allen Zeiten Schwerelosigkeit. Damit befindest du dich immer in einem Inertialsystem. Nach den Einsteinschen Postulaten misst du daher in deinem Labor immer dieselbe Lichtgeschwindigkeit von \(3\cdot 10^{8}\;\mathrm{m/s}\).
Durch die unterschiedliche Größe der Gravitation ändert sich mit der Entfernung zur Erde aber der Gang deiner Uhren in deinem Labor. In der Nähe der Erde geht die Zeit langsamer. Entsprechend muss die Gravitation die Maßstäbe in deinem Labor im selben Ausmaß schrumpfen lassen. Nur so kann die Person im Weltraum-Labor zu allen Zeiten dieselbe konstante Geschwindigkeit von \(c\) messen.
| In der Nähe einer Masse ist jeder Maßstab verkürzt. |
16.9.2 Shapiro-Experiment
Der Einfluss der Gravitation auf den Gang von Uhren kann relativ leicht gezeigt werden (zum Beispiel mit dem Hafele-Keating-Experiment). Trennst du zwei synchronisierte Uhren und bringst sie zu einem späteren Zeitpunkt wieder zusammen, bleibt ein Zeitunterschied bestehen. Bei Maßstäben ist das schon schwieriger. Machst du denselben Versuch mit zwei Maßstäben, stellst du beim erneuten Vergleich am selben Ort fest, dass beide wieder exakt gleich lang sind – Maßstäbe haben in dem Sinne kein „Gedächtnis“.
Wenn sich in der Nähe einer großen Masse Maßstäbe verkürzen, muss der Weg automatisch länger werden. Diese Idee liegt dem Shapiro-Experiment (engl. Shapiro time delay) zugrunde. Dabei wird ein Radarsignal zu einem Planeten geschickt und die Zeit gemessen, bis es als Echo wieder zurückkommt – ähnlich dem Echolot-Verfahren zur Bestimmung der Wassertiefe. Sobald die Sonne sich der Verbindungslinie beider Planeten nähert, sollte sich die Verkürzung der Maßstäbe nahe dem Sonnenrand durch ein Anwachsen der Signallaufzeit bemerkbar machen. Diese Verzögerung wurde von Irwin I. Shapiro in den 1960er-Jahren theoretisch vorhergesagt und auch experimentell bestätigt.
Bild 16.91: Abweichung der normalen Signallaufzeit zwischen Erde und Merkur durch den Einfluss der Sonne
Die Vorhersage der Relativitätstheorie für die Verzögerung des Echos in Abhängigkeit von der Entfernung zur Sonne siehst du in Bild 16.91. Sie nimmt in der Nähe der Sonne steil zu und fällt danach ebenso schnell symmetrisch wieder ab. Dort, wo sich Erde, Sonne und Merkur auf einer Linie befinden, wird das Signal von der Sonne blockiert und die Kurve ist unterbrochen.
16.9.3 Jenseits des Äquivalenzprinzips
Die Äquivalenz von Gravitations- und Trägheitswirkung gilt exakt nur in einem homogenen Gravitationsfeld (Bild 16.92, a). In (b) siehst du die Verhältnisse bei einem sehr großen Labor (oder in der Nähe einer sehr kleinen kompakten Masse). Das Gravitationsfeld ist jetzt deutlich inhomogen und die Beschleunigungsvektoren, die zum Massenmittelpunkt zeigen, sind nicht mehr parallel. In (c) siehst du schließlich die Situation aus der Sicht der Person im fallenden Aufzug: Die Gezeitenkräfte bewirken, dass sich die Körper aufeinander zu bewegen.
Das Äquivalenzprinzip kann das Auftreten des Gezeiteneffekts nicht erklären. Das Äquivalenzprinzip kann also keine vollständige Theorie der Schwerkraft sein. Wir benötigen ein umfassenderes Konzept.
16.9.4 Die 4. Dimension
Du wirst sicher noch wissen, dass die Kreiszahl Pi (\(\pi\)) in der ebenen Geometrie das Verhältnis von Umfang \(U\) zu Durchmesser \(d\) eines Kreises ist (Bild 16.93).
\[\begin{equation} \frac{U}{d}=\pi=3{,}14\ldots \tag{16.27} \end{equation}\]
In Bild 16.94 siehst du einen Kreis, dessen Durchmesser nahe einer großen Masse verläuft. Nach der allgemeinen Relativitätstheorie schrumpfen dort die Maßstäbe. Dadurch haben im Durchmesser jetzt mehr Einheitsstrecken Platz. In unserem Beispiel ist das Verhältnis von Umfang zu Durchmesser zu einer Zahl kleiner als Pi geworden.
\[ \frac{U}{d} =\frac{24}{9} =2{,}66\ldots <\pi \]
Wir können die Situation aber auch anders interpretieren. Wenn alle Maßstäbe gleich lang bleiben sollen, müsste der Durchmesser aus dem Kreis „herausgebeult“ werden, um dasselbe Verhältnis von Umfang zu Durchmesser zu erhalten. Bild 16.95 gibt dir davon eine Vorstellung.
Diese zweite Deutung stammt von Albert Einstein und ist sein berühmtes Konzept des gekrümmten Raumes. Masse verändert dabei die Struktur des Raumes.
Der Kreis in den Bildern oben ist zweidimensional, und die Krümmung des Durchmessers erfolgt in die dritte Dimension (hier nach unten). Aber wohin soll sich ein dreidimensionaler Raum krümmen? Die mathematische Antwort ist einfach: in eine 4. Raumdimension. Dabei gibt es aber ein Problem. Wir können mit 4 Raumdimensionen zwar rechnen, aber vorstellen können wir sie uns nicht. Es geht uns wie den „Flachländern“ im Roman Flatland: A Romance of Many Dimensions von Edwin Abbott Abbott: Sie sind geometrische Wesen in einer zweidimensionalen Welt und können sich die dritte Dimension nicht vorstellen.
Beachte, dass auch diese 4. Dimension eine räumliche Dimension ist. Nimmst du als weitere Dimension die Zeit dazu, hat die Raumzeit der allgemeinen Relativitätstheorie eigentlich 5 Dimensionen.
Links:
- Buch: Flatland: A Romance of Many Dimensions (englisch)
16.9.5 Darstellung der Raumkrümmung
Da wir uns weder eine 4. Raumdimension vorstellen noch darstellen können, reduzieren wir in Darstellungen der Raumkrümmung um eine Dimension. Der Raum wird dann als zweidimensionale Ebene dargestellt, die sich in die dritte Raumdimension krümmt (Gummihautmodell, engl. embedding diagrams, Bild 16.96).
Obwohl sie einen Eindruck der Raumkrümmung vermitteln, sind sie nur eine Analogie – nimm diese Abbildungen also nicht zu „wörtlich“.
16.9.6 Der kürzeste Weg
Die kürzeste Verbindung zwischen zwei Punkten wird in der Geometrie allgemein als Geodäte (engl. geodesic) bezeichnet. In der euklidischen Geometrie ist das die uns vertraute geradlinige Verbindung. Es gibt aber auch andere Geometrien, in denen die Geodäten kurvenförmig sein können.
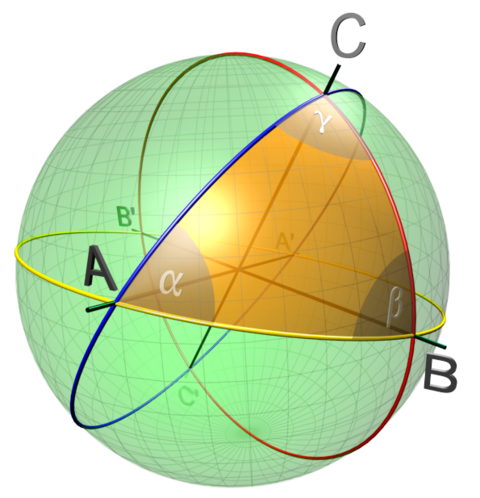
Im Bild 16.97 siehst du das Beispiel einer Kugeloberfläche. Der kürzeste Weg zwischen zwei Punkten A und B verläuft entlang eines Großkreises. Viele Eigenschaften der ebenen Geometrie, die du gewohnt bist, gelten auf gekrümmten Oberflächen nicht mehr – so ist zum Beispiel die Winkelsumme in einem Dreieck nicht mehr 180°, sondern in unserem Fall größer.
In der hyperbolischen Geometrie der Minkowski-Diagramme sind Geodäten noch gerade Strecken. Daher wird die Geometrie der speziellen Relativitätstheorie auch als ebene Raumzeit bezeichnet. In der Geometrie der gekrümmten Raumzeit der allgemeinen Relativitätstheorie (Riemannsche Geometrie) sind die Geodäten im Allgemeinen aber Kurven.
16.9.7 Kräftefreie Bewegung in der gekrümmten Raumzeit
In der klassischen Physik bewegen sich kräftefreie Körper entlang von Geraden. In der gekrümmten Raumzeit der allgemeinen Relativitätstheorie gilt aber:
| Jeder kräftefreie Körper bewegt sich entlang einer Geodäte. |
Wenn du also auf der Erde einen Gegenstand wirfst und dabei eine parabelförmige Bahn beobachtest, dann bewegt er sich kräftefrei entlang einer Geodäte in der gekrümmten Raumzeit (16.98). Und die Ursache für die Raumkrümmung ist die Erde.
Bild 16.98: Fall eines Apfels: (a) beschleunigt als Folge der Gravitationskraft (b) gleichförmig (kräftefrei) in der gekrümmten Raumzeit.
Die Gravitation ist also nach der allgemeinen Relativitätstheorie keine Kraft, sondern einfach die Folge der gekrümmten Raumzeit-Geometrie. John Archibald Wheeler, ein Student von Einstein, fasste das so zusammen: „Spacetime tells matter how to move; matter tells spacetime how to curve“ (Die Raumzeit bestimmt, wie sich Materie bewegt; Materie bestimmt die Krümmung der Raumzeit).
Das Newtonsche Gravitationsgesetz ist durch die allgemeine Relativitätstheorie nicht überflüssig geworden. Für die meisten alltäglichen Berechnungen ist es nach wie vor eine ausgezeichnete Näherung.
16.9.8 Ist die Gravitation eigentlich eine Kraft?
In der Allgemeinen Relativitätstheorie wird die Wirkung der Gravitation als Eigenschaft der Raumzeit gedeutet. Ist die Gravitation dann eigentlich noch eine Kraft?
Das ist eine sehr interessante Frage und hauptsächlich davon abhängig, was wir unter dem Begriff „Kraft“ verstehen wollen. Wir haben Kraft als ein Modell kennengelernt, mit dessen Hilfe wir Wechselwirkungen zwischen Körpern beschreiben können. In diesem Sinn ist die Gravitation natürlich eine Kraft, ebenso wie die Scheinkräfte – die Trägheitskräfte, die durch die Wahl eines beschleunigten Bezugssystems auftreten.
Die geometrische Interpretation der Gravitationskraft war nur der Anfang. In der theoretischen Physik kann heute auch die Wirkung der elektrischen Kraft als Krümmung einer abstrakten Raumzeit interpretiert werden, sodass geladene Teilchen den Geodäten in dieser abstrakten Raumzeit folgen. Die sogenannten Eichtheorien, die die schwache und starke Wechselwirkung beschreiben, sind – wie die Allgemeine Relativitätstheorie – ebenfalls zutiefst geometrische Theorien.
16.9.9 Periheldrehung des Merkurs
Der Merkur durchläuft keine exakte Ellipsenbahn. Der sonnennächste Punkt der Bahn (Perihel) bewegt sich weiter und es entsteht eine Rosettenbahn (Bild 16.99). Dieses Phänomen – das auch bei anderen Planeten zu beobachten ist – wird als Periheldrehung bezeichnet.
Die Periheldrehung des Merkurs kann in der Newtonschen Himmelsmechanik durch den Einfluss der anderen Planeten im Sonnensystem erklärt werden. Allerdings gibt es eine winzige Abweichung: Die gemessene Drehung ist um 0,43 Bogensekunden pro Jahr größer als der berechnete Wert. Im 19. Jahrhundert wurde daher ein bis dahin unentdeckter Planet mit Namen „Vulkan“ angenommen, dessen Einfluss den Unterschied erklären sollte.
Die Gleichungen der Relativitätstheorie liefern den exakten Wert für die Periheldrehung des Merkur, auch ohne weiteren Planet. Dieser Erfolg bestärkte Albert Einstein im Glauben an die Richtigkeit seiner Theorie – lange vor den ersten gezielten experimentellen Bestätigungen.
16.9.10 Quellen der Gravitation
Die Quelle von Gravitation ist nach dem Newtonschen Gravitationsgesetz einzig und alleine die Masse von Körpern.
In der Relativitätstheorie sind dagegen Masse, Energie und Impuls untrennbar miteinander verknüpft. Daher beeinflusst nicht nur die Masse an sich, sondern auch ihr Bewegungszustand (zum Beispiel ihre Rotation) die Krümmung der Raumzeit. Noch genauer: In der allgemeinen Relativitätstheorie verändern Masse, Energie, Impuls, Druck und Spannung die Krümmung der Raumzeit. In der mathematischen Formulierung der Relativitätstheorie sind all diese Größen nur Aspekte einer allgemeineren physikalischen Größe, dem Energie-Impuls-Tensor.
16.9.11 Lense-Thirring-Effekt
Der Lense-Thirring-Effekt (engl. frame-dragging-effect) – benannt nach Josef Lense und Hans Thirring) – beschreibt den Einfluss einer rotierenden Masse auf die Raumzeit. Dabei kannst du dir die Raumzeit wie eine zähe Flüssigkeit vorstellen und die Masse wie eine Kugel, die in ihr schwimmt. Rotiert die Kugel, wird die Flüssigkeit am Rand der Kugel mitbewegt – die Raumzeit wird verdrillt (Bild 16.100).
Der Lense-Thirring-Effekt hervorgerufen durch die Rotation der Erde, konnte durch den Forschungssatelliten Gravity Probe B 2011 mit einer Abweichung von \(1\,\%\) bestätigt werden. Aufgrund der kleinen Masse der Erde – verglichen mit einem Stern oder einem schwarzen Loch – ist dieser Effekt unglaublich klein und die Messung eine Meisterleistung.
16.9.12 Gravitationslinseneffekt
Schon beim Experiment von Eddington hast du gesehen, dass Licht durch Gravitation abgelenkt wird und sich die (scheinbare) Sternposition aufgrund der Masse im Vordergrund verändert. Die Wirkung der Masse ist dabei ähnlich der einer optischen Linse. Dieser Effekt wird daher allgemein als Gravitationslinseneffekt (engl. gravitational lensing) bezeichnet.
Die Aufnahme in Bild 16.101 stammt vom Hubble-Weltraumteleskop und zeigt eine rote Galaxie im Vordergrund. Der umgebende Ring ist das durch Gravitation verzerrte Bild einer weit dahinter gelegenen blauen Galaxie. Albert Einstein hat solche Gravitationslinseneffekte bereits vorausgesagt. Ihm zu Ehren werden solche Erscheinungen „Einstein-Ringe“ genannt. Durch den Gravitationslinseneffekt kommt es nicht immer zu Ring-Erscheinungen. Oftmals kommt es zu Mehrfachbildern. Dann ist ein und dasselbe astronomische Objekt an unterschiedlichen Stellen mehrmals am Nachthimmel zu sehen, wie zum Beispiel beim Einsteinkreuz.
Aus der Form der durch Gravitation entstandenen Bilder kann auf die Größe und Verteilung der Massen im Vordergrund geschlossen werden. Insbesondere bietet der Gravitationslinseneffekt damit eine Möglichkeit, die Verteilung der sogenannten dunklen Materie zu messen. Mit diesem Begriff wird Masse bezeichnet, die kein Licht aussendet und nur durch ihre Gravitationswirkung beobachtet werden kann.
16.9.13 Gravitationswellen
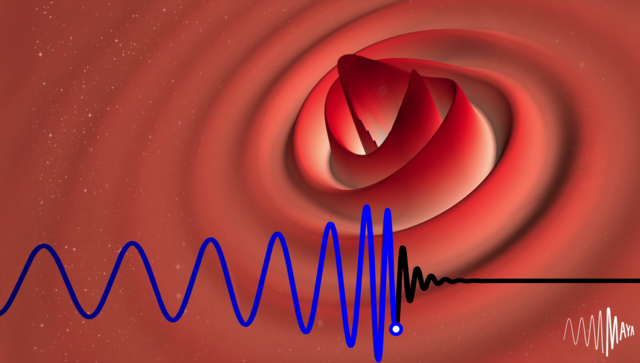
So wie sich die Störung einer Wasseroberfläche als Welle ausbreitet, sollte sich nach der allgemeinen Relativitätstheorie auch die Störung in der Raumzeit ausbreiten. Die Effekte von Gravitationswellen (engl. gravitational waves) sind derart klein, dass sie erst rund 100 Jahre nach der Vorhersage Albert Einsteins experimentell nachgewiesen werden konnten.
Der erste Nachweis gelang 2016 am LIGO (Laser-Interferometer Gravitationswellen-Observatorium). Die Anlage gleicht einem riesigen Interferometer mit mehreren Kilometern Länge. Dabei wurde das charakteristische Muster von Gravitationswellen gemessen, wie sie bei der Verschmelzung zweier umeinander kreisender schwarzer Löcher entstehen (Bild 16.102).
Links:
16.9.14 Einstein-Rosen-Brücke
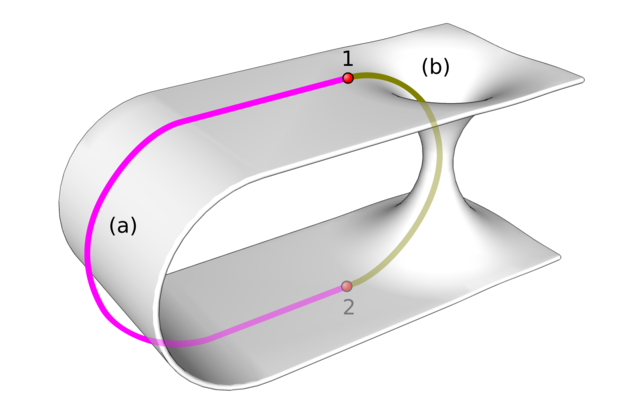
Verwenden wir wieder das Gummihautmodell für die gekrümmte Raumzeit, dann kann ein Wurmloch wie in Bild 16.103 dargestellt werden.
Eine extreme Raumkrümmung verbindet dabei zwei weit entfernte Punkte der Raumzeit durch eine Art Tunnel. Dieser Tunnel in der Raumzeit heißt „Wurmloch“ oder Einstein-Rosen-Brücke (engl. Einstein-Rosen bridge) – benannt nach Albert Einstein und Nathan Rosen. Sie ist in der Science-Fiction ein beliebtes Mittel, die maximal mögliche Reisegeschwindigkeit von \(c\) zu umgehen und so sehr große Entfernungen in kurzer Zeit zu überbrücken. Was sagt die Physik dazu?
Einstein-Rosen-Brücken widersprechen nicht den Gleichungen der Relativitätstheorie. Umgekehrt kann daraus aber nicht geschlossen werden, dass es ein solches Phänomen in der Natur auch tatsächlich geben muss.
Für eine so große Raumkrümmung ist eine unglaublich große Menge an Masse/Energie notwendig. Eine Einstein-Rosen-Brücke zu erzeugen oder auch nur zu kontrollieren, läge jenseits von unseren Möglichkeiten.
Selbst wenn wir eine Einstein-Rosen-Brücke entdecken würden, können wir nicht hindurchreisen. Die Gezeitenkräfte bei der Annäherung an ein Wurmloch wären so groß, dass es jeden Körper zerreißen würde (das wird scherzhaft als „Spaghettifizierung“ bezeichnet).
So faszinierend die Vorstellung von Einstein-Rosen-Brücken auch ist, für Reisen im Weltraum könnten wir sie – sollte es sie wirklich geben – nicht verwenden.
