17.10 Kräfte aus quantenmechanischer Sicht
Der Large Hadron Collider am europäischen Kernforschungszentrum ist einer der leistungsstärksten Teilchenbeschleuniger (Bild 17.98). Über 10.000 Personen aus über 100 Staaten sind bei diesem internationalen Großprojekt beteiligt.
Und wozu dieser Mega-Aufwand? Mit diesen riesigen Maschinen hoffen wir, die noch offenen Fragen zum Aufbau der Materie und den Kräften in der Natur beantworten zu können. So konnte zum Beispiel 2012 das Higgs-Teilchen – nachdem es 35 Jahre zuvor vorhergesagt wurde – tatsächlich nachgewiesen werden.
Links:
17.10.1 Quantenfeldtheorie
Die Beschreibung von Kräften durch Felder ist extrem erfolgreich. Die Maxwell-Gleichungen beschreiben das elektromagnetische Feld, und auch die Relativitätstheorie verwendet Feldgleichungen, um die Gravitationskraft zu beschreiben. Da schien es nur naheliegend, auch in der Quantenmechanik ein Feldkonzept für die Beschreibung von Kräften zu verwenden. Die Quantenfeldtheorie (QFT) (engl. quantum field theory) hat es sich zur Aufgabe gemacht, das Feldkonzept der klassischen Physik für die Beschreibung der Wechselwirkung von Quantenobjekten anzupassen.
In der Quantenmechanik werden Objekte nicht mehr durch Ort und Impuls, sondern durch sogenannte Wellenfunktionen \(\psi (x,y,z,t)\) beschrieben. Da zu jedem Zeitpunkt ein Wert an jedem Raumpunkt angegeben werden kann, erfüllt eine Wellenfunktion ebenfalls das Kriterium für ein Feld. Alle Wellen der Form \(\psi(x,y,z,t)\) besitzen nach den Gesetzen der Quantenmechanik auch Teilcheneigenschaften wie Masse oder Spin. Diese Feldquanten werden daher auch als Wechselwirkungs„teilchen“ (Eichbosonen) bezeichnet.
Nach der Vorstellung der QFT sind alle Teilchen nichts anderes als angeregte Zustände (engl. field excitations oder particle states) der ihnen zugrunde liegenden Quantenfelder, die fundamentaler als die Teilchen selbst sind. Diese fundamentalen Felder sind aber nicht direkt messbar. Nur die sich aus ihnen ergebenden Größen wie Ladungen, Energien oder Geschwindigkeit können gemessen werden. Allerdings gibt es unterschiedliche Beschreibungen („Konfigurationen“) desselben unbeobachtbaren Feldes, die zu gleichen Werten bei den beobachtbaren Größen führen. Eine Transformation von einer solchen Feldkonfiguration in eine andere wird als Eichtransformation (engl. gauge transformation) bezeichnet. Ändern sich die Werte der beobachtbaren Größen unter einer Eichtransformation nicht, werden die Felder als eichinvariant (engl. gauge invariance) bezeichnet. Da jede Invarianz unter einer Transformation als „Symmetrie“ betrachtet werden kann, wird eine eichinvariante Transformation auch als Eichsymmetrie (engl. gauge symmetry) bezeichnet.
Im Kapitel über Elektrizität hast du das elektrische Feld E und das elektrische Potenzialfeld \(\phi\) kennengelernt. Während sich das elektrische Vektorfeld über die Kraft messen lässt, ist das Potenzialfeld prinzipiell unbeobachtbar. Außerdem sind nur Potenzial-Differenzen physikalisch bedeutsam. Addierst du zum Potenzial eine konstante Zahl, würde sich an den beobachtbaren elektrischen Größen nichts ändern – der Nullpunkt bei einem Potenzialfeld ist beliebig wählbar. Der Umstand, dass die additive Konstante im Potenzial frei wählbar ist (wie ein beliebiger Maßstab „geeicht“ werden kann), brachte Hermann Weyl dazu, die Begriffe Eichtransformation, Eichinvarianz und Eichsymmetrie zu verwenden.
Zurzeit lassen sich mit diesem angepassten Feldkonzept alle fundamentalen Wechselwirkungen mit Ausnahme der Gravitation sehr genau vorhersagen.
17.10.2 Eichbosonen
In der Teilchenphysik wird die Kraftübertragung von einem Teilchen auf ein anderes durch den Austausch von Wechselwirkungsteilchen (Eichbosonen, engl. gauge bosons) beschrieben. Jede Kraft hat ihr eigenes Austauschteilchen:
| Wechselwirkung | relative Stärke | Reichweite | Austauschteilchen | Masse | Spin |
|---|---|---|---|---|---|
| Stark | \(1\) | \(\approx10^{-15}\) | Gluonen | \(\approx0\) | 1 |
| Elektromagentisch | \(10^{-2}\) | \(\infty\) | Photon | 0 | 1 |
| Schwach | \(10^{-13}\) | \(\approx10^{-17}\) | Z-,W-Bosonen | \(>80\;\mathrm{GeV}\) | 1 |
| Gravitation | \(10^{-39}\) | \(\infty\) | Graviton (hypothetisch) | 0 | 2 |
In der Tabelle kannst du erkennen: je größer die Masse des Austauschteilchens, desto geringer die Reichweite der Kraft. Damit ist auch geklärt, warum wir aus dem Alltag nur die elektromagnetische und die Gravitationskraft kennen. Die Reichweite der starken Wechselwirkung entspricht in etwa dem Abstand von Nukleonen in einem Atomkern, die der schwachen Wechselwirkung sogar noch weit darunter.
Eine durch den Austausch von Teilchen übertragene abstoßende Kraft lässt sich noch vorstellen: Spielen zwei Personen einander einen schweren Ball abwechselnd zu, ist beim Wegwerfen und auch beim Fangen jedes Mal ein Kraftstoß spürbar. Im Rahmen der Quantenmechanik können auch anziehende Kräfte durch Austauschteilchen beschrieben werden, allerdings gibt es dafür keinen so anschaulichen Vergleich mehr.
17.10.3 Virtuelle Teilchen
Bei den Austauschteilchen handelt es sich nicht um normale Teilchen, sondern um sogenannte virtuelle Teilchen. Diese sind weder sichtbar noch direkt messbar – sie machen sich nur durch ihre Wechselwirkung bemerkbar. Du kannst dir den virtuellen Zustand eines Teilchens am ehesten als einen kurzlebigen Zwischenzustand vorstellen, der nur während einer Wechselwirkung zweier Teilchen auftritt.
Aber wie kann ein Elektron ständig virtuelle Photonen aussenden, ohne Masse oder Energie zu verlieren? Nach der Heisenbergsche Unschärferelation gilt: Um ein Photon der Energie \(E\) messen zu können, muss es mindestens für die Dauer von \(\Delta t\) lang existieren, wobei \(\Delta t\cdot E\approx h/2\pi\) gilt. Für ein grünes Photon mit der Energie \(2\;\mathrm{eV}\) ist das rund \(10^{-15}\;\mathrm{s}\). Virtuelle Photonen existieren nur so lange, wie es das Unschärfeprinzip zulässt, ohne dass sie nachgewiesen werden können. Trifft das virtuelle Photon innerhalb dieser Zeit auf eine andere Ladung, wird es von dieser absorbiert. Andernfalls gehen Energie und Impuls des virtuellen Photons wieder auf die aussendende Ladung zurück.
Je weniger Energie das virtuelle Photon hat, desto länger kann es existieren und desto weiter kann es sich daher fortbewegen. Die Energie des Photons hängt nur von seiner Frequenz ab und die kann beliebig klein sein. Dies ist einerseits der Grund dafür, dass die elektrische Kraft zwischen Ladungen mit der Entfernung abnimmt und andererseits die Reichweite unbegrenzt ist.
Daraus ergibt sich auch noch eine andere interessante Folge: Das reine Vakuum ist gar nicht so leer, wie du dir vielleicht bisher vorgestellt hast. Nach der Quantenfeldtheorie treten an jedem Ort im Universum ständig Quantenfluktuationen auf (Vakuumfluktuationen) , also entstehen aus dem Nichts virtuelle Teilchen und verschwinden nach kürzester Zeit wieder.
17.10.4 Elektrische Kraft
Die elektrische Kraft wirkt zwischen elektrischen Ladungen. Die Kraftübertragung erfolgt durch (virtuelle) Photonen. Da ihre Masse null ist, hat die elektrische Kraft unendliche Reichweite. Da Photonen selbst keine elektrische Ladung besitzen, wird die Ladung der Wechselwirkungspartner nicht verändert. Der Zweig der Quantenphysik, der sich mit der elektrischen Wechselwirkung beschäftigt, heißt Quantenelektrodynamik (QED).
17.10.5 Starke Wechselwirkung
Die starke Kraft oder starke Wechselwirkung (auch Farbkraft, engl. strong nuclear force) wirkt zwischen Quarks und damit auch zwischen allen Teilchen, die aus Quarks bestehen (Hadronen). Insbesondere ist sie damit für die Bindung zwischen Nukleonen (zwischen Neutronen und Protonen) im Atomkern verantwortlich. Die Kraftübertragung erfolgt durch Gluonen. Der Name leitet sich vom englischen Begriff glue für Klebstoff her. Die starke Kraft hat theoretisch unbegrenzte Reichweite, da Gluonen keine Masse haben. Alle aus Quarks gebildeten Teilchen sind farbneutral – die Farbladung nach außen hin also abgeschirmt. Somit wirkt die starke Kraft praktisch nur im Inneren von Hadronen und ist auf eine Reichweite von etwa \(10^{-15}\;\mathrm{m}\) begrenzt.
Nach der Quantenchromodynamik QCD gibt es acht Gluonen, die alle masselos sind und Spin 1 haben. Sechs der Gluonen besitzen eine Farbladung, die sich immer aus einer „Farbe“ und einer „Antifarbe“ zusammensetzt (Bild 17.99). Zwei weitere sind dagegen „farblos“ (Bild 17.99).
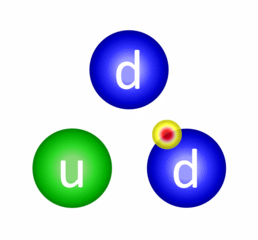
In der Animation 17.100 siehst du als Beispiel die Wechselwirkung innerhalb eines Neutrons. Die Gluonen sind dargestellt als Punkte mit der Farbladung im Zentrum und der Antifarbe am Rand. Zum Beispiel stößt ein grünes up-Quark ein grün/anti-rotes Gluon aus und wird dadurch rot. Trifft dieses Gluon auf ein rotes down-Quark, wird seine Farbladung mit der anti-roten Farbladung des Gluons aufgehoben und übernimmt die verbleibende grüne Farbladung. Durch den Austausch eines Gluons ändert sich die Farbladung beider wechselwirkenden Quarks. Nur ein Austausch von „farblosen“ Gluonen ändert die Farbladung der beteiligten Quarks nicht.
Gluonen können aber auch direkt mit anderen Gluonen wechselwirken, sodass Teilchen existieren könnten, die nur aus Gluonen bestehen, die Glueballs.
17.10.6 Schwache Kraft
Die schwache Kraft oder schwache Wechselwirkung (engl. weak nuclear force) wirkt zwischen Leptonen, Quarks und Hadronen – also zwischen allen Teilchen bis auf Eichbosonen. Sie ist um Größenordnungen kleiner als die elektrische oder die starke Wechselwirkung. Treten diese Kräfte auf, ist die schwache Wechselwirkung vernachlässigbar. Sie zeigt sich daher besonders deutlich bei Neutrinos, weil sie weder eine elektrische Ladung noch eine Farbladung besitzen.
Die drei Austauschteilchen der schwachen Wechselwirkung sind das neutrale Z-Boson sowie ein positiv und ein negativ geladenes W-Boson. Alle Austauschteilchen der schwachen Kraft besitzen Masse, daher hat sie eine extrem kurze Reichweite unterhalb eines Atomkernradius (weniger als \(10^{-18}\;\mathrm{m}\)).
Die schwache Kraft kann keine gebundenen Systeme bilden. Im Gegenteil: Sie ist für den Zerfall (oder treffender gesagt: für die Umwandlung) von Hadronen und Leptonen verantwortlich. Das bekannteste Beispiel ist der Betazerfall, bei dem ein Neutron in ein Proton, ein Elektron und ein Elektron-Antineutrino umgewandelt wird. Teilchen-Umwandlungen sind nur dann möglich, wenn dabei kein Erhaltungssatz verletzt wird.
17.10.7 Umwandlungen von Teilchen
Im Mikrokosmos finden ständig Umwandlungen von Teilchen statt. Dabei lassen sich prinzipiell zwei Arten von Umwandlungen unterscheiden:
- spontane Umwandlungen eines Teilchens in mehrere Folgeteilchen („Teilchenzerfall“) und
- angeregte Umwandlungen, bei der durch Zusammenstöße von zwei oder mehreren Teilchen neue Teilchen entstehen.
Die Art der möglichen Umwandlungen wird dabei nur durch die Erhaltungssätze eingeschränkt.
17.10.7.1 Spontane Teilchenumwandlung
Ein typisches Beispiel für eine spontane Umwandlung ist der „Beta-Zerfall“ eines Neutrons in ein Proton, ein Elektron und ein Elektron-Antineutrino.
\[ n^0 \quad \rightarrow \quad p^+ \; + \; e^- + \; \overline{\nu}_e \]
Das Elektron-Antineutrino ist notwendig, damit die Leptonenzahl vor und nach der Umwandlung erhalten bleibt (in unserem Fall null bleibt).
Warum haben wir das Wort „Zerfall“ in diesem Abschnitt stets in Anführungszeichen gesetzt? Weil der Begriff etwas irreführend ist. Denn der Begriff „Zerfall“ lässt fälschlicherweise vermuten, dass in unserem Beispiel Protonen und Elektronen fixe Bestandteile von Neutronen sind. Das ist aber nicht der Fall. In einem Atomkern kann sich zum Beispiel auch ein Proton in ein Neutron, ein Positron und ein Elektron-Neutrino umwandeln („Beta-Minus-Zerfall“).
\[ p^+ \quad \rightarrow \quad n^0 \; + \; e^+ + \; \nu_e \]
Die Masse des entstandenen Neutrons ist sogar größer als die Masse des ursprünglichen Protons. Die zusätzliche Masse stammt von der verminderten Bindungsenergie des Tochterkerns – schließlich befindet sich ein Proton weniger im Kern und die Abstoßung der Kernteilchen ist insgesamt geringer. Diese Umwandlung kann daher auch nicht bei einem isolierten Neutron stattfinden. Du siehst: Von einem „Zerfall“ im Sinne von „in seine Bestandteile zerfallen“, kann also keine Rede sein.
17.10.7.2 Angeregte Teilchenumwandlung
Bei der angeregten Teilchenumwandlung wird ein Umwandlungsprozess durch das gleichzeitige Zusammentreffen von zwei oder mehreren Teilchen ausgelöst. Die kinetische Energie der Ausgangsteilchen kann dabei teilweise oder vollständig in Masse der Folgeteilchen umgewandelt werden. Hier einige Beispiele für Umwandlungsprozesse bei der Kollision von zwei Protonen:
\[ \begin{aligned} p^+ \; + \; p^+ \quad \rightarrow \quad {} & p^+ \; + \; p^+ \; + \; e^- \; + \; e^+ \\ p^+ \; + \; p^+ \quad \rightarrow \quad {} & p^+ \; + \; p^+ \; + \; \pi^0 \\ p^+ \; + \; p^+ \quad \rightarrow \quad {} & p^+ \; + \; n^0 \; + \; \pi^+ \\ p^+ \; + \; p^+ \quad \rightarrow \quad {} & \ldots \\ \end{aligned} \]
Prinzipiell kann jeder Umwandlungsprozess auch in die umgekehrte Richtung ablaufen, also zum Beispiel:
\[ p^+ \; + \; n^0 \; + \; \pi^+ \quad \rightarrow \quad p^+ \; + \; p^+ \]
Allerdings ist die Wahrscheinlichkeit, dass gleich drei Teilchen mit den richtigen Eigenschaften an einem Ort zusammentreffen, wesentlich geringer. Entsprechend seltener wird diese Umwandlung in der Natur beobachtet.
17.10.8 Feynman-Diagramm
In der Teilchenphysik werden sogenannte Feynman-Diagramme für die abstrakte, bildliche Darstellung von Wechselwirkungen verwendet.
Für Feynman-Diagramm gelten folgende Regeln:
- Wechselwirkungsteilchen werden als wellen-, spiralförmige oder strichlierte Linien dargestellt.
- Alle anderen Teilchen werden als Pfeile in der Zeit dargestellt.
- Anti-Teilchen sind durch Pfeile gegen die Zeitrichtung gekennzeichnet.
- Aus der Pfeilrichtung kann nicht auf anziehende oder abstoßende Kräfte geschlossen werden!
Die Richtung der Zeitachse ist leider nicht einheitlich. In manchen Diagrammen verläuft sie von unten nach oben, in anderen von links nach rechts.
In Bild 17.101 siehst du das Feynman-Diagramm zur Wechselwirkung von zwei Elektronen durch den Austausch eines virtuellen Photons (\(\gamma\)). Die Zeitachse verläuft von links nach rechts.
In Bild 17.102 siehst du das Feynman-Diagramm für den Zerfall eines Neutrons in ein Proton (Beta-Zerfall). Das down-Quark im Neutron sendet ein \(\mathrm{W^-}\)-Boson aus und wird zu einem up-Quark – das ganze Teilchen zu einem Proton. Das \(\mathrm{W^-}\)-Boson kann wegen seiner großen Masse nicht lange bestehen und zerfällt in ein Elektron (\(\mathrm{e^-}\)) und ein Elektron-Anti-Neutrino (\(\mathrm{\bar{\nu}_e}\)). Beachte den Pfeil gegen die Zeitrichtung für das Anti-Teilchen.
In der Relativitätstheorie ist uns das Myonenschauer Experiment untergekommen. In Bild 17.103 siehst du das Feynman-Diagramm für den häufigsten Zerfall eines Myons in ein Myon-Neutrino, ein Elektron-Antineutrino und ein Elektron. Beachte, dass die Zeitachse dieses Mal von unten nach oben verläuft. Der Pfeilrichtung des Anti-Teilchen zeigt wieder gegen die Zeitrichtung.
17.10.9 Gravitationskraft
Die Gravitationskraft wirkt zwischen Massen, daher auf alle Elementarteilchen. Da die Gravitationskraft im Verhältnis zu den restlichen Kräften allerdings um Zehnerpotenzen kleiner ist, kann sie in der Teilchenphysik fast immer vernachlässigt werden.
Nach Vorstellung der Quantenfeldtheorie (QFT) erfolgt die Kraftübertragung – wie bei allen anderen Kräften – durch Austauschteilchen, den sogenannten Gravitonen. Da die Reichweite der Gravitationskraft – wie die der elektrischen Kraft – unbegrenzt ist, kann daraus geschlossen werden, dass die Masse von Gravitonen ebenfalls null ist. Der eindeutige Nachweis einzelner Gravitonen erscheint aktuell nicht möglich. Die Wahrscheinlichkeit für die Wechselwirkung einzelner Gravitonen ist so gering, dass der Bau eines ausreichend großen Detektors unsere Möglichkeiten bei Weitem übersteigt.
Das erfolgreichste Modell der Gravitation ist nach wie vor die Raum-Zeit-Krümmung. Die theoretischen Physikerinnen und Physiker versuchen, die Quantenfeldtheorie und die Allgemeine Relativitätstheorie in Einklang zu bringen. Diese Theorie der Quantengravitation (QG) befindet sich derzeit noch in der Entwicklung.
17.10.10 Higgs Boson
Im Standardmodell werden Kräfte durch den Austausch von Eichbosonen beschrieben. Im Jahr 1964 wurde zum Standardmodell eine mathematisch konsistente Theorie entwickelt, die verlangte, dass alle Wechselwirkungsteilchen masselos sind. Die Experimente zeigen allerdings, dass die Wechselwirkungsteilchen der schwachen Kraft – die W- und Z-Bosonen – große Massen haben. In der Folge wurde eine Lösung für das Problem von theoretischen Physikerinnen und Physikern gefunden, die Brout-Englert-Higgs-Mechanismus genannt wird. Er beschreibt, wie die grundlegende Eigenschaft der Masse von Elementarteilchen zustande kommt. Nach dieser Theorie gibt es ein weiteres bisher unbekanntes Feld, das sogenannte Higgs-Feld. Die Masse von W- und Z-Bosonen, aber auch die Masse aller anderen (massebehafteten) Elementarteilchen wie Elektronen und Quarks, wird als Folge der Wechselwirkung mit dem Higgs-Feld erklärt. Mit diesem Ansatz wurde es möglich, die schwache und die elektromagnetische Wechselwirkung als zwei verschieden starke Aspekte einer einzigen grundlegenden elektroschwachen Wechselwirkung zu beschreiben.
Das Higgs-Feld ist zwar nicht direkt messbar, aber die Theorie sagt voraus, dass bei großen Energien ein weiteres Elementarteilchen entsteht, das sogenannte Higgs-Teilchen. Bei Experimenten am CERN wurde 2012 ein neues Teilchen im Massenbereich von etwa \(125\;\mathrm{GeV}\) gefunden, dessen Eigenschaften mit denen des Higgs-Bosons übereinstimmten. 2013 erhielten François Englert und Peter Higgs, nachdem das neue Feld und das neue Teilchen benannt sind, für die Entwicklung des Higgs-Mechanismus den Nobelpreis.
Der Großteil der Masse im Universum stammt allerdings nicht vom Higgs-Feld. Das Proton hat eine Masse von \(1{,}67\cdot 10^{-27}\;\mathrm{kg}\) oder rund \(938{,}3\;\mathrm{MeV/c^2}\). Bildest du die Summe der Massen der Bausteine (zwei Up-Quarks zu je \(2{,}3\;\mathrm{MeV/c^2}\) und ein Down-Quark mit \(4{,}8\;\mathrm{MeV/c^2}\)), erhältst du gerade einmal etwa \(1\,\%\) der Masse des Protons. Fast die gesamte Masse des Protons besteht aus Bindungsenergie durch die starke Wechselwirkung.
17.10.11 Kopplungskonstante
Vielleicht hast du dich in der Übersicht über die Kräfte gewundert, wie die Werte für die relative Stärke zustande gekommen sind. Gravitation wirkt auf Massen, während die elektromagnetische Kraft nur auf elektrische Ladungen wirkt. Diese beiden Kräfte vergleichen zu wollen, scheint wie der Versuch, Äpfel mit Motorsägen zu vergleichen.
In der theoretischen Physik gelang es, die Wirkung der vier Grundkräfte mithilfe von dimensionslosen Faktoren, den sogenannten Kopplungskonstanten, zu formulieren. Ihre Werte sind ein Maß für die Größe der jeweiligen Kraftart. Diese Konstanten werden aus Messungen der Wahrscheinlichkeit einer Wechselwirkung bei der Begegnung zweier Teilchen ermittelt.
Trotz des Wortes „Konstante“ im Namen variieren ihre Werte bei der Wechselwirkung mit unterschiedlichen Teilchen leicht. Die Werte für die Kopplungskonstanten sind also nur Durchschnittswerte. Messungen ergeben für die Verhältnisse der Kopplungskonstanten:
\[\begin{equation} \textstyle\alpha_\mathrm{s}: \textstyle\alpha_\mathrm{em}: \textstyle\alpha_\mathrm{W}: \textstyle\alpha_\mathrm{G} =1:10^{-2}:10^{-13}:10^{-39} \tag{17.38} \end{equation}\]
Die starke Kraft ist danach rund 100-mal stärker als die elektromagnetische Kraft, \(10^{-13}\)-mal stärker als die schwache Kraft und \(10^{-39}\)-mal stärker als die Schwerkraft. Die Kopplungskonstante für die elektromagnetische Kraft \(\textstyle\alpha_\mathrm{em}\) wird auch Feinstrukturkonstante genannt.
17.10.12 Weltformel
Bei Experimenten der Hochenergiephysik zeigen die Kopplungskonstanten ein interessantes Verhalten. Bei sehr großen Energien nähern sich die Werte der Kopplungskonstante von schwacher und elektromagnetischer Wechselwirkung einander an (Bild 17.104).

Bild 17.104: Die Kopplungskonstanten \(\alpha\) der vier Grundkräfte als Funktion der Energie \(E\).
In den 1960er-Jahren gelang es, die schwache und die elektromagnetische Wechselwirkung in einer Theorie zusammenzufassen. Laut dieser Theorie sind die beiden Kräfte nur zwei Aspekte einer einzigen grundlegenden Wechselwirkung (elektroschwachen Wechselwirkung, engl. electroweak interaction).
In Bild 17.104 kannst du sehen, dass auch die Kopplungskonstanten der anderen Wechselwirkungen eine ähnliche Tendenz bei großen Energien zeigen. Nach der Urknalltheorie (engl. big bang theory) war die Temperatur im Universum umso höher, je weiter die Zeit zurückgedreht wird, bis schließlich der Urknall erreicht wird. Im frühen Universum könnte es daher wirklich nur eine einzige Urkraft gegeben haben, die sich erst durch das allmähliche Abkühlen des Universums in die vier Grundkräfte, so wie wir sie heute kennen, aufgespalten hat.
Theoretische Physikerinnen und Physiker versuchen daher alle vier Grundkräfte durch einen einzigen mathematischen Formalismus zu beschreiben. Eine Theorie, die zusätzlich die starke Wechselwirkung beschreibt, wird große vereinheitlichte Theorie (engl. Grand Unified Theory oder kurz GUT) genannt. Eine Theorie, die sogar alle vier Grundkräfte vereint, wird Theorie von Allem oder Weltformel (engl. Theory of Everything, kurz TOE) genannt.
17.10.13 Stringtheorie
Das Standardmodell ist eine sehr erfolgreiche Theorie. Es bietet eine vollständige, korrekte, konsistente und elegante Beschreibung der bekannten Elementarteilchen und ihrer Wechselwirkungen. Das Standardmodell wurde durch zahlreiche Experimente bestätigt. Kein Experiment widerspricht ihm. Trotzdem sind nicht alle glücklich damit. Im Standardmodell sind zwar keine Fehler aufgetreten, aber viele Fragen bleiben unbeantwortet. Warum sind beispielsweise Top-Quarks etwa eine Billion Mal massereicher als Neutrinos? Was stabilisiert die Masse des Higgs-Bosons? Warum gibt es genau drei Gruppen von Fermionen? All das lässt sich nicht auf einige wenige Grundprinzipien zurückführen, sondern wirkt willkürlich.
Physikerinnen und Physiker sind also auf der Suche nach einer Erweiterung des Standardmodells, die diese Fragen beantworten kann. Eine dieser Erweiterungen ist die Stringtheorie (engl. string theory). Darin besteht jedes Teilchen aus jeweils einem einzigen winzigen vibrierenden Energie-Faden (String). Alle Fäden sind gleich, aber je nachdem, wie der Faden schwingt, beobachten wir ein Elektron oder ein anderes Teilchen. So wie jede Schwingung einer Gitarrensaite einem anderen Ton entspricht, entspricht jedes Schwingungsmuster eines Strings einem anderen Teilchen im Standardmodell (Bild 17.105).
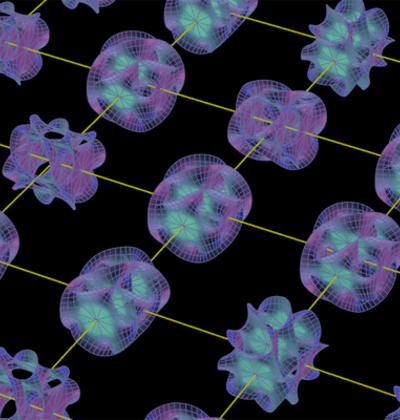
Bild 17.106: Calabi-Yau-Mannigfaltigkeit, zu der die sechs Extradimensionen in jedem Punkt der Raumzeit „aufgerollt“ sind
Nach der Auffassung der Stringtheorie benötigen wir 10 Dimensionen, um die Natur zu beschreiben. Zusätzlich zu den uns vertrauten vier Dimensionen (drei Raum- und eine Zeitdimension) sagt die Stringtheorie sechs weitere Raumdimensionen voraus. Diese Extradimensionen sollen in jedem Punkt der Raumzeit extrem kompakt – etwa in der Größenordnung der Planck-Länge (\(\approx 10^{-35}\;\mathrm{m}\)) – „aufgerollt“ sein (Bild 17.106). Sie machen sich daher nur auf extrem kleinen Skalen bemerkbar. Im Alltag können wir nur die üblichen drei Raumdimensionen erkennen.
Links:
17.10.14 M-Theorie
Ende des 20. Jahrhunderts gab es schon fünf unterschiedliche Stringtheorien. 1995 sorgte Edward Witten bei einer Konferenz für Aufsehen, als er eine neue Theorie vorstellte, die er M-Theorie nannte. Dabei handelt es sich nicht um eine weitere Stringtheorie, sondern um eine übergeordnete Theorie, die alle bisherigen Stringtheorien und auch die Supergravitation (11d SUGRA) vereint (Bild 17.107).

Bild 17.107: M-Theorie als Verbindung der Stringtheorien (Type I, Type IIA, IIB, Hel E8 und Hel SO(32))
Wie bei einem Ambigramm ergeben sich die unterschiedlichen Stringtheorien, wenn die M-Theorie aus unterschiedlichen Blickwinkeln betrachtet wird (Bild 17.108). Die M-Theorie ist ein Fortschritt, weil sich gewisse Probleme in einigen Stringtheorien einfacher lösen lassen als in anderen. Mithilfe der „Übersetzungsregeln“ der M-Theorie (den sogenannten Dualitäten) lassen sich diese Probleme von einer Stringtheorie in eine andere übertragen.
Das „M“ im Namen könnte für Membran stehen. Denn spezielle Membranen (sogenannte Branes) sind ein neues Konzept der M-Theorie. Dabei handelt es sich um zweidimensionale Objekte, die in einer höherdimensionalen Raumzeit existieren sollen. Branes können sowohl miteinander als auch mit den eindimensionalen Strings wechselwirken. Zum Beispiel können offene Strings an Branes enden und somit Kräfte übertragen. Für die Beschreibung ist dann noch eine weitere Raumdimension notwendig. Sie ist sozusagen der „Klebstoff“, der die verschiedenen Stringtheorien vereint. Nach der M-Theorie besteht damit unser Universum sogar aus 11 Dimensionen.
Die M-Theorie beschreibt alle vier Grundkräfte in einem Formalismus und ist aktuell der aussichtsreichste Kandidat für eine vereinheitlichte Theorie. Allerdings gibt es im Moment keine einzige Vorhersage des Modells, die sich experimentell überprüfen und damit ihre Richtigkeit zeigen lässt.
17.10.15 Wie geht es weiter?
Ende des 19. Jahrhunderts gab es in der Physikgemeinschaft die vorherrschende Meinung, dass alle grundlegenden physikalischen Gesetze bereits entdeckt waren. Lediglich ein paar kleine Probleme galt es noch zu lösen. Darunter etwa die Frage nach der Stabilität von Atomen, die Frage nach dem Lichtäther oder der photoelektrische Effekt. Doch diese scheinbar „kleinen Unstimmigkeiten“ führten in den Jahrzehnten danach zur Entwicklung der Relativitätstheorie und der Quantenmechanik, die unser Weltbild vollkommen verändert haben.
Obwohl wir heute mehr von der Natur verstehen als jemals zuvor, ist die Liste der ungelösten Probleme in der Physik seitdem nicht kürzer, sondern sogar länger geworden. Auch wenn es aktuell wieder so aussieht, als wären alle fundamentalen Gesetze gefunden und es nur eine Frage der Zeit ist, bis eine Möglichkeit gefunden wird, die Stringtheorie experimentell nachzuweisen – wir könnten uns auch irren! Auch die besten Physikerinnen und Physikern stellen Theorien und Modelle auf, die sich im Experiment als falsch erweisen. Aber auch diese scheinbaren Misserfolge, helfen neue Erkenntnisse über die Natur zu gewinnen. Denke zum Beispiel an den negativen Ausgang beim Michelson-Morley-Experiment, der letztlich zur Entwicklung der Relativitätstheorie führte.

Bild 17.109: Physikerin beim Aufbau eines Experiments, bei dem ein neuartiger Lichtwellenleiter, der Informationen noch schneller übertragen können soll, getestet wird.
Aber auch abgesehen davon gibt es für Physikerinnen und Physiker jede Menge zu tun. Einige der aktuell wichtigsten Forschungsgebiete sind die Plasma- und Fusionsforschung, die Entwicklung von Quantencomputern oder die Festkörperphysik, die sich mit den Eigenschaften und Formen von Materie im festen Aggregatzustand befasst, wie etwa der Hochtemperatur-Supraleitung.
Du siehst: Die Physik hört niemals auf, spannend zu sein. Je genauer wir hinsehen und je mehr wir herausfinden, desto mehr entdecken wir, was wir noch nicht über die Natur wissen. Und vielleicht gehörst ja gerade du in ein paar Jahren zu den Personen, die mit dem Nobelpreis für Physik ausgezeichnet werden und die ihren Namen neben Persönlichkeiten wie Marie Curie, Albert Einstein oder Erwin Schrödinger wieder finden. Also: Hör niemals auf, neugierig zu sein!