10.5 Radioaktivität
In Bild 10.46 siehst du einen sogenannten Geigerzähler. Mit diesem Messgerät kann radioaktive Strahlung festgestellt werden. In der Nähe einer radioaktiven Substanz hörst du ein unregelmäßiges Klicken (Audio abspielen).
Bisher ging es fast immer nur um die Atomhülle. In diesem Kapitel widmen wir uns ausschließlich den Atomkernen. Du wirst erfahren, was der Begriff „Radioaktivität“ bedeutet, was in einer Nuklidkarte verzeichnet ist, durch welches Gesetz der zufällige radioaktive Zerfall von Kernen beschrieben werden kann und was das Klicken des Geigerzählers bedeutet.
10.5.1 Radioaktiver Zerfall
Die meisten chemischen Elemente besitzen mehrere Isotope. Befinden sich zu viele oder zu wenige Neutronen in einem Kern, wird er „unrund“. Er gibt Energie ab und wandelt sich dabei in ein anderes Atom um. Dieser Vorgang wird radioaktiver Zerfall (engl. radioactive decay) und die Atome als radioaktiv (engl. radioactive) bezeichnet.
Durchläuft die abgegebene Strahlung ein elektrisches Feld, können drei unterschiedliche Anteile radioaktiver Strahlung unterschieden werden, die Alpha (\(\alpha\)), Beta (\(\beta\)) und Gamma (\(\gamma\)) genannt wurden (Bild 10.47).
Alpha-Strahl (rot): Wird in Richtung der negativen Platte abgelenkt. Es muss sich dabei um positiv geladene Teilchen handeln.
Beta-Strahl (blau): Wird in Richtung der positiven Platte abgelenkt. Es muss sich dabei um negativ geladene Teilchen handeln.
Gamma-Strahl (schwarz): wird nicht abgelenkt, ist daher elektrisch neutral.
10.5.2 Alpha-Zerfall
Bei einem Alpha-Zerfall (engl. alpha decay) stößt der radioaktive Kern einen Helium-Kern (\({}^{4}_2\mathrm{He}\), \(\alpha\)-Teilchen) ab (Bild 10.48).
Die Massenzahl verringert sich dabei um vier (zwei Protonen und zwei Neutronen) und die Kernladungszahl um zwei. Dabei ändert das Atom das Element. Als Beispiel siehst du im Bild oben die Umwandlung von Radium-226 (Ordnungszahl 88) in Radon-222 (Ordnungszahl 86).
\[ {}^{226}_{\,\,88}\mathrm{Ra}\ \overset{\alpha}{\longrightarrow}\ {}^{222}_{\,\,86}\mathrm{Rn} +{}^{4}_2\mathrm{He} \]
10.5.3 Beta-Zerfall
Bei einem Beta-Zerfall (engl. beta decay) wandelt sich ein Neutron in ein Proton um. Die Masse und die Ladung gleicht ein Elektron aus, das ebenfalls bei dieser Umwandlung entsteht und aus dem Kern ausgestoßen wird (Bild 10.49) – es stammt also nicht aus der Atomhülle!
Da nur ein Nukleon in ein anderes Nukleon umgewandelt wird, bleibt die Massenzahl unverändert. Die Kernladungszahl steigt um eins. Auch beim Beta-Zerfall ändert sich das Element. Im Bild oben siehst du den Zerfall von Cäsium-137 (Ordnungszahl 55) zu Barium-137 (Ordnungszahl 56).
\[ {}^{137}_{\,\,55}\mathrm{Cs}\ \overset{\beta}{\longrightarrow}\ {}^{137}_{\,\,56}\mathrm{Rn} +e^{-} \]
Umgekehrt kommt es auch vor, dass ein Proton in ein Neutron umgewandelt wird. In diesem Fall wird ein Positron (positiv geladenes Elektron, Anti-Elektron) aus dem Kern ausgestoßen und die Kernladungszahl sinkt um eins. Dieser Prozess wird \(\beta^+\)-Zerfall genannt – im Gegensatz zum \(\beta^-\)-Zerfall, bei dem ein negativ geladenes Elektron ausgestoßen wird.
10.5.4 Gamma-Zerfall
Nach einem Alpha-Zerfall oder Beta-Zerfall hat der neue Kern oft noch überschüssige Energie. Der radioaktive Kern gibt diese Energie in Form eines Gamma-Quants (Photon oder Lichtteilchen mit sehr hoher Energie) ab (Bild 10.50).
Beim Gamma-Zerfall (engl. gamma decay) findet keine Kernumwandlung statt.
10.5.5 Nuklidkarte
Die Kerne aller Atomarten (Nuklide) sind in der Nuklidkarte (engl. chart of nuclides) (Bild 10.51) aufgelistet. Die Protonenzahl steigt nach oben und die Neutronenzahl steigt nach rechts. Stabile Isotope sind schwarz eingezeichnet, instabile Nuklide farbig, wobei die Farbe über die Art des Zerfalls Auskunft gibt.
Alle Isotope eines Elements befinden sich waagrecht nebeneinander. Im Periodensystem entspricht ein Feld einer ganzen Zeile in der Nuklidkarte.
Entlang der \(45^\circ\)-Gerade (\(\mathrm{N}=\mathrm{Z}\)) befinden sich die Nuklide, die gleich viele Protonen wie Neutronen besitzen. Während für niedrige Ordnungszahlen die Anzahl der Protonen und Neutronen in einem stabilen Kern gleich groß ist, sind für größere Kerne mehr Neutronen als Protonen notwendig.
Der Grund für diese Asymmetrie ist die unterschiedliche Reichweite von elektrischer Kraft und Kernkraft (Starke Wechselwirkung). Während die Reichweite der abstoßenden elektrischen Kraft unbegrenzt ist, wirkt die anziehende Kernkraft nur zwischen Nukleonen in unmittelbarer Nähe (Bild 10.52).
10.5.6 Zerfallsreihen
Der bei einem radioaktiven Zerfall entstandene Kern kann selbst wieder radioaktiv sein. Der Kern zerfällt wiederholt, bis er schließlich ein stabiles Nuklid erreicht. Die Serie an Nukliden, die ein Kern durchläuft, bis er stabil ist, wird Zerfallsreihe (engl. decay chain) genannt.
In Bild 10.53 siehst du ein Beispiel für eine solche Zerfallsreihe, die Uran-Actinium-Reihe. Sie beginnt bei dem radioaktiven Isotop Uran-235 und endet bei dem stabilen Isotop Blei-207.
10.5.7 Radioaktive Quellen
Radioaktivität ist Teil unseres täglichen Lebens. Zum Beispiel befinden sich geringe Mengen Radon in der Luft und Uran und Thorium im Erdreich.
Radioaktive Strahlung zählt zur ionisierenden Strahlung und schädigt Zellen. Mit der natürlichen Strahlenbelastung haben alle Organismen auf der Erde leben gelernt – wir verfügen über ausreichend Reparatur-Mechanismen, um gesund zu bleiben.
Zu einem gesundheitlichen Problem kommt es dann, wenn wir über diese natürliche Strahlenbelastung hinaus radioaktiver Strahlung ausgesetzt sind. Die Endprodukte bei der Kernspaltung, wie sie in Kernkraftwerken anfallen, sind zum Beispiel radioaktiv. Gelangen diese radioaktiven Stoffe in die Umwelt, führt das zu schweren gesundheitlichen Schäden.
Schwach radioaktive Substanzen werden auch in der Medizin verwendet, zum Beispiel bei der Untersuchung von Stoffwechselvorgängen (Tracer-Prinzip).
10.5.8 Abschirmung radioaktiver Strahlung
Alpha- und Betastrahlung bestehen aus Teilchen. Trotz großer Bewegungsenergie haben sie nur ein kleines Durchdringungsvermögen. Alphastrahlung kann schon durch ein Blatt Papier abgehalten werden und Betastrahlung durch ein dünnes Aluminiumblech (Bild 10.54).
Am schwersten lässt sich Gammastrahlung abschirmen. Sie kommt in unterschiedlich großen Energiewerten vor. Je größer die Energie, desto tiefer dringt Gammastrahlung in die Materie ein. Zur Abschirmung werden üblicherweise dicke Platten aus Blei verwendet.
10.5.9 Spontaner Zerfall
Der Zerfall eines radioaktiven Atoms ist absolut zufällig („spontan“). Er kündigt sich weder vorher an, noch lässt sich der Zeitpunkt des Zerfalls auf irgendeine Weise beeinflussen (weder durch Temperaturänderung, noch durch chemische Prozesse). Der Geigerzähler (Bild 10.46) macht diesen zufälligen Zerfall hörbar.
Dieser Zufall ist sehr erstaunlich. Egal ob in der Mechanik oder in der Elektrizitätslehre – nichts passiert zufällig, alles hat eine Ursache. Und selbst in der Thermodynamik, wo so viele Teilchen am Werk sind, dass wir mit Statistik arbeiten müssen (Kinetische Gastheorie), könnten wir doch jede Kollision der Gasteilchen zumindest im Prinzip erklären.
Was die Physikerinnen und Physiker lange nicht wussten: Der zufällige radioaktive Zerfall ist eine der wenigen Fälle, bei dem der Quanten-Charakter des Mikrokosmos im Alltag erkennbar wird. Heute wissen wir: Im Bereich der Atome und darunter ist alles zufällig!
10.5.10 Halbwertszeit
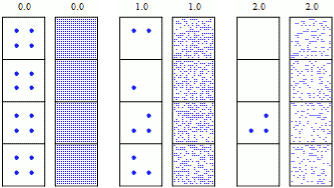
Auch wenn ein einzelner Zerfall eines radioaktiven Isotops vollkommen zufällig und unvorhersehbar ist, lässt sich das Verhalten einer großen Menge derselben radioaktiven Kerne – dank Statistik – sehr gut vorhersagen (Gesetz der großen Zahlen). In der Simulation 10.56 siehst du auf der linken Seite Kästchen mit anfänglich 4 und auf der rechten Seite Kästchen mit 400 radioaktiven Kernen. Der Zustand der rechten Seite ist kaum vorhersehbar, aber in den Kästchen auf der rechten Seite ist die Anzahl der verbleibenden Kerne ungefähr gleich groß.
Für eine große Menge gleicher Isotope gibt es eine charakteristische Halbwertszeit \(t_{1/2}\) (engl. half-life) also einen Zeitraum, in dem rund die Hälfte aller ursprünglich vorhandenen Kerne zerfallen sind. Im interaktiven Bild 10.57 siehst du den Zusammenhang von Halbwertszeit und verbleibenden Kernen (abfallende Exponentialfunktion). Nach etwa 10 Halbwertszeiten sind nur mehr \(0{,}1\,\%\) des ursprünglichen Materials vorhanden – die Aktivität einer Strahlenquelle wird dann als vernachlässigbar angesehen.
Die Werte für die Halbwertszeiten der unterschiedlichen Isotope sind sehr unterschiedlich. Der Bereich reicht von extrem kurzen Halbwertszeiten von \(10^{−22}\) Sekunden (zum Beispiel Lithium-4) bis zu extrem langen Halbwertszeiten von mehreren Billiarden Jahren (zum Beispiel Kalzium-48).
Links:
10.5.11 Zerfallsgesetz
Hast du zu Beginn \(N_0\) identische radioaktive Kerne, kannst du mit dem Zerfallsgesetz (engl. exponential decay) berechnen, wie viele Kerne \(N\) nach der Zeit \(t\) noch übrig sind. Es lautet:
| \[\begin{equation} N(t)=N_{0}\cdot {\mathrm e}^{{-\lambda t}} \tag{10.5} \end{equation}\] |
Die Anzahl folgt also einer abfallenden Exponentialfunktion. In dieser Formel bedeuten:
- \(N(t)\), die Anzahl der Kerne nach der Zeit \(t\) („Stück“, also dimensionslos)
- \(N_0\) die ursprüngliche Anzahl der Kerne („Stück“, also dimensionslos)
- \(e\), die Eulersche Zahl (\(2{,}71\ldots\))
- \(\lambda\), die Zerfallskonstante (in \(\mathrm{1/s}\))
- \(t\), die verstrichene Zeit (in \(\mathrm{s}\))
Die Zerfallskonstante \(\lambda\) (Lambda) hängt vom jeweiligen Nuklid ab. Die Zerfallskonstante ist nicht die Halbwertszeit. Du kannst aber beide Konstanten mithilfe des natürlichen Logarithmus ineinander umrechnen.
\[\begin{equation} \lambda = \ln(2)\cdot T_{1/2} \tag{10.6} \end{equation}\]
10.5.12 Herleitung des Zerfallsgesetzes
Unterschiedliche radioaktive Nuklide zerfallen in unterschiedlichen Raten. Für alle gilt jedoch: Je größer die Anzahl der Kerne, desto größer ist die Anzahl der Zerfälle pro Zeiteinheit. Mathematisch lässt sich das durch
\[ \frac{dN}{dt} = -\lambda\cdot N \]
ausdrücken. Die Konstante \(\lambda\) (Zerfallskonstante) ist charakteristisch für das jeweilige Nuklid. Umformen liefert:
\[ \begin{aligned} \frac{dN}{dt} = {} & -\lambda\cdot N \qquad\Bigr\rvert\cdot \frac{dt}{N} \\ \frac{dN}{N} = {} & -\lambda\cdot dt \\ \end{aligned} \]
Bilden wir das bestimmte Integral vom Zeitpunkt 0, bei dem \(N_0\) Kerne vorhanden sind bis zu einer Zeit \(t\), zu der nur noch \(N\) Kerne übrig sind, dann erhalten wir:
\[ \int_{N_0}^N\frac{dN}{dt} = -\lambda\int_0^t dt \]
Lösen des Integrals liefert:
\[ \ln\left({\frac {N}{N_{0}}}\right) = -\lambda t \]
Wenden wir die Exponentialfunktion auf beiden Seiten an und berücksichtigen, dass \(\mathrm{e}^{\ln(x)}=x\) ergibt, erhalten wir:
\[ \mathrm{e}^{-\lambda t}={\frac {N}{N_{0}}}\qquad\Bigr\rvert\cdot N_0 \]
Und schließlich das Zerfallsgesetz:
\[ N=N_{0}\cdot\mathrm{e}^{-\lambda t} \]
10.5.13 Radiokarbonmethode zur Altersbestimmung
Eine wichtige Anwendung von radioaktiver Strahlung ist die Altersbestimmung von organischen Proben mithilfe der Radiokarbonmethode (C-14 Methode). Luft enthält nicht nur das stabile Kohlenstoffisotop C-12, sondern auch das radioaktive Isotop C-14. Es handelt sich dabei um einen \(\beta\)-Strahl mit einer Halbwertszeit von 5730 Jahren:
\[\begin{equation} {}^{14}_6\mathrm{C}\ \overset{\beta}{\longrightarrow}\ {}^{14}_7\mathrm{N} +\mathrm {e^{-}} \tag{10.7} \end{equation}\]
In der Atmosphäre befinden sich beide Isotope. Auf der einen Seite zerfallen ständig radioaktive C-14 Kerne, auf der anderen Seite entstehen in den oberen Schichten der Atmosphäre durch kosmische Strahlung ständig neue C-14 Kerne. Insgesamt ist ihre Konzentration über große Zeiträume konstant. C-12 und C-14 verhalten sich chemisch gleichwertig. Alle Lebewesen nehmen daher beide Isotope im Körper auf, solange sie leben. Das Verhältnis von C-12 und C-14 im Körper ist dasselbe wie in der Luft. Sobald ein Organismus stirbt (Zeitpunkt der „Fixierung“), ändert sich dieses Verhältnis. Während die C-12 Atome alle erhalten bleiben, verringert sich durch den radioaktiven Zerfall die Anzahl der C-14 Atome. Das Verhältnis von C-12 zu C-14 Atomen ist also ein Maß für das Alter der Probe.
Mit diesem Verfahren lässt sich das Alter von organischen Materialien im Bereich zwischen 300 und etwa 60.000 Jahren bestimmen. Zum Beispiel wurde der Todeszeitpunkt der Gletschermumie „Ötzi“ (Bild 10.58) mithilfe der Radiokarbonmethode auf etwa 3200 v. d. Z. datiert.
10.5.14 Transmutation
Nach der Vorstellung Alchemisten war der Stein der Weisen (engl. philosopher’s stone) – eine bestimmte Substanz – der Schlüssel zur „Herstellung“ von Gold aus unedlen Metallen, wie zum Beispiel Blei oder Quecksilber (Bild 10.59). Heute wissen wir, dass alle Versuche der Alchemisten zur Goldsynthese scheitern mussten. Denn die gesamte Chemie spielt sich in der Atomhülle ab. Um jedoch das Element eines Atoms zu ändern, muss dessen Atomkern verändert werden.
.jpeg){kind=link}
Die sogenannte Transmutation (Kernumwandlung, engl. nuclear transmutation) ist eigentlich ein ganz alltägliches Phänomen. Sie findet zum Beispiel beim Alpha- oder Beta-Zerfall von selbst statt. Ist es aber gezielt möglich, ein Element in Gold zu verwandeln? Dies gelang erstmals Glenn Seaborg im Jahr 1980. Dabei wurden im Labor einige Tausend Atome Bismut in das einzige stabile Gold Isotop Au-197 umgewandelt. Mithilfe eines Teilchenstrahls aus einem Zyklotrons wurden Protonen und Neutronen aus den schweren Bismut-Atomen entfernt. Die Kosten für so eine Umwandlung sind jedoch astronomisch hoch. Deshalb ist es unwirtschaftlich, Gold auf diese Weise künstlich zu erzeugen.
