13.3 Bahnen geladener Teilchen in Magnetfeldern
Die Leuchterscheinung in Bild 13.24 wird Nordlicht oder aurora borealis genannt.

Bild 13.24: Polarlicht nahe dem Nordpol (Video)
Im Kapitel Ladungen in Magnetfeldern hast du über die Kräfte von geladenen Teilchen in Magnetfeldern erfahren. In diesem Kapitel betrachten wir die Bahnen der Teilchen, die sich daraus ergeben, und wie Polarlichter zustande kommen.
13.3.1 Kreisbahn in einem homogenen Magnetfeld
In Bild 13.25 siehst du die Bahn eines Protons, dessen Geschwindigkeitsrichtung im rechten Winkel zu den Feldlinien eines homogenen Magnetfeldes steht – es entsteht eine kreisförmige Bahn.
Die Lorentzkraft steht zu allen Zeiten im rechten Winkel auf den Geschwindigkeitsvektor und ist immer gleich groß. Die konstante Lorentzkraft wirkt als Zentripetalkraft und zwingt das Proton auf eine Kreisbahn.
Da \(\vec{v}\) und \(\vec{F}_L\) immer rechtwinkelig aufeinander stehen, wird zu keiner Zeit Beschleunigungsarbeit vom Feld verrichtet. Die Bewegung ändert nur die Richtung, sie wird aber weder schneller noch langsamer.
Um den Bahnradius für diese Bewegung zu erhalten, setzen wir die Lorentzkraft gleich der Zentripetalkraft:
\[ \begin{aligned} F_L = {} & F_Z \\ Q\cdot v\cdot B = {} & \frac{m\cdot v^2}{r} &&\Bigr\rvert\cdot r \\ r\cdot Q\cdot v\cdot B = {} & m\cdot v^2 &&\Bigr\rvert\cdot \frac{1}{Q\cdot v\cdot B} \\ r = {} & \frac{m\cdot v^{\cancel{2}}}{Q\cdot \cancel{v}\cdot B} \\ \end{aligned} \]
Durch Kürzen erhalten wir den Ausdruck:
| \[\begin{equation} r = \frac{m\cdot v}{Q\cdot B} \tag{13.5} \end{equation}\] |
13.3.2 Schraubenbahn in einem homogenen Magnetfeld
Schließen Geschwindigkeitsvektor und Magnetfeldlinien einen Winkel \(\alpha\) ungleich 90° ein, ist die Bahn eine Schraubenlinie (Bild 13.26).
Der Geschwindigkeitsvektor \(\vec{v}\) kann in zwei Komponenten zerlegt werden: eine Komponente normal und eine Komponente parallel zu den magnetischen Feldlinien:
- \(\vec{v}_\perp\): hier wirkt die Lorentzkraft, diese Komponente sorgt für die Kreisbewegung
- \(\vec{v}_\parallel\): bleibt unbeeinflusst von dem Magnetfeld und sorgt für den Hub (Steigung) der Schraubenlinie.
Wie bei der Kreisbahn in einem homogenen Magnetfeld wird auch in diesem Fall keine Arbeit an dem Teilchen verrichtet.
13.3.3 Fadenstrahlrohr
In Bild 13.27 siehst du die Kreisbahn eines geraden Elektronenstrahls in einem Fadenstrahlrohr (engl. teltron tube), wie er durch ein homogenes Magnetfeld abgelenkt wird.
Im Hintergrund kannst du eine Spule des Helmholtz-Spulen-Paares erkennen, die für ein homogenes Magnetfeld im Bereich der Kathodenröhre sorgt.
Mithilfe einer solchen Anordnung konnte schon um 1900 das Verhältnis von Elektronenladung zu Elektronenmasse (\(e/m_e\)) ermittelt werden.
Wird die Röhre in der Halterung leicht verdreht, stehen Geschwindigkeitsrichtung und Magnetfeldrichtung nicht mehr im rechten Winkel zueinander und die dabei entstehende Schraubenbahn lässt sich mit dem Fadenstrahlrohr ebenfalls deutlich beobachten.
Links:
- Simulation: Fadenstrahlrohr Versuch
- Video: Fadenstrahlrohr
13.3.4 Bestimmung der spezifischen Ladung des Elektrons
Das Verhältnis von Ladung zu Masse (\(q/m\)) eines Teilchens wird als spezifische Ladung (engl. mass-to-charge ratio) bezeichnet, im Falle des Elektrons bedeutet das den Quotienten aus Elementarladung und Elektronenmasse \(e/m_e\). Aus dem Ablenkversuch mit dem Fadenstrahlrohr lässt sich dieses Verhältnis berechnen.
Für die Kreisbahn eines Elektrons in einem homogenen Magnetfeld gilt:
\[ \begin{aligned} \frac{m_e\cdot v}{e\cdot B} = {} & r\qquad\Bigr\rvert\cdot \frac{e\cdot B}{m_e} \\ v = {} & \frac{r\cdot e\cdot B}{m_e} \\ \end{aligned} \]
Die Geschwindigkeit \(v\) erhält das Elektron beim Durchlaufen einer Beschleunigungsspannung \(U\), bevor es das Magnetfeld erreicht. Durch Gleichsetzen von kinetischer Energie und elektrischer Arbeit des Elektrons (Energieerhaltungssatz) erhalten wir:
\[ \begin{aligned} {\frac {1}{2}}\cdot m_e\cdot v^{2} = {} & e\cdot U \qquad\Bigr\rvert\cdot \frac{2}{m_e} \\ v^{2} = {} & \frac{2\cdot e\cdot U}{m_e} \\ \end{aligned} \]
In diese Gleichung setzen wir den Ausdruck für \(v\) aus der Beziehung oben ein.
\[ \begin{aligned} \left(\frac{r\cdot e\cdot B}{m_e}\right)^{2} = {} & \frac{2\cdot e\cdot U}{m_e} \\ \frac{r^2\cdot e^2\cdot B^2}{m_e^2} = {} & \frac{2\cdot e\cdot U}{m_e}\qquad\Bigr\rvert\cdot \frac{m_e}{r^2\cdot e\cdot B^2} \\ \frac{e}{m_e}=\frac{2\cdot U}{r^{2}\cdot B^{2}} \end{aligned} \]
Alle Größen auf der rechten Seite der Gleichung – also die magnetische Flussdichte \(B\), der Bahnradius \(r\) und die Beschleunigungsspannung \(U\) – können durch Messung bestimmt und so die spezifische Ladung berechnet werden.
Nach demselben Prinzip kann die spezifische Ladung von beliebigen geladenen Teilchen bestimmt werden.
Links:
13.3.5 Zyklotron
Das Zyklotron ist ein Teilchenbeschleuniger und besteht aus zwei halbkreisförmigen Dosen („Dees“). Ein konstantes senkrechtes Magnetfeld sorgt durch die Lorentzkraft für die Ablenkung normal zur Bewegungsrichtung der geladenen Teilchen. Durch ein elektrisches Wechselfeld zwischen den Dees werden die geladenen Teilchen im Spalt zwischen den Dees kurzfristig beschleunigt und bewegen sich auf immer größer werdenden Halbkreisen immer weiter nach außen, bis sie mit maximaler Geschwindigkeit die Austrittsöffnung erreichen (Bild 13.28).
Der Bahnradius eines Teilchens in einem homogenen Magnetfeld ist
\[ r = \frac{m\cdot v}{Q\cdot B} \]
und nimmt proportional mit der Geschwindigkeit \(v\) zu. Für die Umlaufdauer \(T\) gilt:
\[ \begin{aligned} T = {} & \frac{2\cdot\pi\cdot r}{v} \\ = {} & \frac{2\cdot\pi}{v}\cdot \frac{m\cdot v}{Q\cdot B} \\ = {} & \frac{2\cdot\pi\cdot m}{Q\cdot B} \\ \end{aligned} \]
Durch den Kehrwert der Umlaufdauer erhalten wir die Zyklotronfrequenz \(f_Z\):
| \[\begin{equation} f_Z = \frac{Q\cdot B}{2\cdot\pi\cdot m} \tag{13.6} \end{equation}\] |
Sie ist unabhängig von der Geschwindigkeit des Teilchens! Das Teilchen kann also mit einer konstanten Wechselfrequenz zwischen den Dees immer weiter beschleunigt werden.
Zyklotrone können bis zu einem Durchmesser von rund \(5\;\mathrm{m}\) gebaut werden. Protonen können dabei auf eine Energie von etwa \(100\;\mathrm{eV}\) (Elektronenvolt) beschleunigt werden.
13.3.6 Synchrotron
Moderne Teilchenbeschleuniger werden als Synchrotron gebaut. Im Gegensatz zu einem Zyklotron besteht ein Synchrotron aus einem mehreren Kilometern langen hohlen Ring, in dem die Ladungen durch elektrische Felder entlang des Ringes beschleunigt werden.
Mit ansteigender Geschwindigkeit muss – bei konstantem Bahnradius – die nötige Zentripetalkraft vergrößert werden. Das bedeutet, dass die Lorentzkraft (=Zentripetalkraft) beim Beschleunigen mit der Teilchengeschwindigkeit synchronisiert werden muss; daher der Name Synchrotron.

Bild 13.29: Lage des unterirdischen LHC Teilchenbeschnleunigers
Im Bild 13.29 siehst du den Large Hadron Collider, einen Teilchenbeschleuniger des europäischen Kernforschungszentrums CERN bei Genf mit einer Länge von \(27\;\mathrm{km}\)! Protonen können damit auf eine Energie von etwa \(13\;\mathrm{TeV}\) (Tera-Elektronenvolt) beschleunigt werden – sie bewegen sich dann fast mit Lichtgeschwindigkeit.
Links:
- Website: CERN online entdecken (Englisch)
13.3.7 Massenspektrograph
In der Natur kommt jedes chemische Element als Isotopengemisch vor. Zum Beispiel besteht natürlicher Kohlenstoff aus einer Mischung von \(\text{C-}12\) (\(\sim 98{,}94\,\%\)), \(\text{C-}13\) (\(\sim 1{,}06\,\%\)) und Spuren von \(\text{C-}14\). Durch die gleiche Kernladungszahl verhalten sich Isotope eines Elements chemisch vollkommen identisch. Sie unterscheiden sich nur in ihrer Masse.
Um die Mengenanteile der einzelnen Isotope eines Elements zu ermitteln, kann ein Massenspektrograph (engl. mass spectrograph) wie in Bild 13.30 verwendet werden. Alle Isotope werden mit derselben Geschwindigkeit in ein homogenes Magnetfeld geschossen. Aufgrund der identischen Ladung der Isotope eines Elements und der gleichen Geschwindigkeit ist die Lorentzkraft bei jedem Isotop gleich groß. Je größer die Masse, desto größer fällt ihr Bahnradius aus.
\[ r = \frac{v}{Q\cdot B}\cdot m \]
Auf einem Auffangbildschirm kann anhand der Lage des Auftreffpunktes die Isotopen-Sorte ermittelt werden. Die Helligkeit des Auftreffpunktes gibt Auskunft über die Häufigkeit dieses Isotops.
Um zu gewährleisten, dass alle Isotope beim Erreichen der Ablenkkammer dieselbe Geschwindigkeit besitzen, passieren die Teilchen zuvor einen Geschwindigkeitsfilter.
13.3.8 Geschwindigkeitsfilter
Ein Geschwindigkeitsfilter (engl. velocity selector) verwendet ein gekreuztes magnetisches und elektrisches Feld, um nur Ionen mit einer bestimmten Geschwindigkeit aus einem Ionenstrahl durch eine Lochblende passieren zu lassen (Bild 13.31).
Sind die Feldrichtungen wie in Bild 13.31 angeordnet, werden positiv geladene Teilchen durch die Coulombkraft nach unten und durch die Lorentzkraft nach oben abgelenkt. Sind beide Kräfte gleich groß, heben sie einander auf und die Bahn des Teilchens ist gerade. Setzen wir die Coulombkraft \(F_\text{C}\) und die Lorentzkraft \(F_\text{L}\) gleich, erhalten wir:
\[ \begin{aligned} F_{{\text{C}}} = {} & F_{{\text{L}}} \\ q\cdot E = {} & q\cdot v\cdot B \\ E = {} & v\cdot B \\ \end{aligned} \]
Und für die Passiergeschwindigkeit \(v_{{\text{0}}}\)
| \[\begin{equation} v_{{\text{0}}}={\frac{E}{B}} \tag{13.7} \end{equation}\] |
Während die Coulombkraft nur von der Ladung abhängt, ist die Lorentzkraft von der Ladung und der Geschwindigkeit eines Teilchens abhängig. Ist die Geschwindigkeit größer als \(v_0\) (\(v>v_0\)), überwiegt die Lorentzkraft und das Teilchen wird nach oben abgelenkt. Ist die Geschwindigkeit kleiner als \(v_0\) (\(v<v_0\)), ist die Lorentzkraft kleiner als die Coulombkraft und das Teilchen wird nach unten abgelenkt.
Für den Filterprozess spielt die Masse der Teilchen keine Rolle. Daher wird diese Art von Filter zum Beispiel bei Massenspektrographen verwendet.
13.3.9 Teilchenbahn in einem inhomogenen Magnetfeld
Bisher haben wir nur die Bahnen von geladenen Teilchen in homogenen magnetischen Feldern betrachtet. In Bild 13.32 siehst du ein Elektron, das sich von links einem Nordpol eines Stabmagneten spiralförmig nähert.
Der B-Feld-Vektor besteht aus zwei Komponenten: \(\vec{B}_2\) radial zur Symmetrieachse des Magnetfeldes und \(\vec{B}_1\) normal dazu. Zeigt die Geschwindigkeitsrichtung des Elektrons in das Bild hinein, sorgt die Lorentzkraft \(\vec{F}_2\) – hervorgerufen durch die Komponente \(\vec{B}_2\) – für die Zentripetalkraft. Die Lorentzkraft \(\vec{F}_1\) – hervorgerufen durch die Komponente \(\vec{B}_1\) – wächst bei Annäherung an den Pol und bewirkt eine vom Pol wegweisende Beschleunigung. Das Elektron nähert sich dem Nordpol in einer immer enger werdenden Spiralbahn, bis sich schließlich seine Richtung umkehrt und es sich vom Pol wieder weg bewegt. Dabei folgt es einer gegensinnigen Spiralbahn. Aus einer Rechtsdrehung wird eine Linksdrehung und umgekehrt.
Bei diesem Vorgang ändert das Elektron zwar ständig die Bewegungsrichtung, der Geschwindigkeitsbetrag (Schnelligkeit) bleibt dabei aber unverändert. Nur ein elektrisches Feld kann den Geschwindigkeitsbetrag einer Ladung ändern!
Diese Anordnung wird als magnetischer Spiegel (engl. magnetic mirror) bezeichnet. Befinden sich zwei magnetische Spiegel gegenüber, lassen sich zwischen ihnen geladene Teilchen „einsperren“. Sie pendeln zwischen den beiden magnetischen Spiegeln hin und her, wie Licht bei einem optischen Spiegel. Die Anordnung wird magnetische Flasche (engl. magnetic bottle) genannt.
13.3.10 Magnetosphäre der Erde
Im Abschnitt Magnetfeld der Erde haben wir das Magnetfeld nahe der Erdoberfläche betrachtet. Das Magnetfeld reicht jedoch weit in den Weltraum hinein.
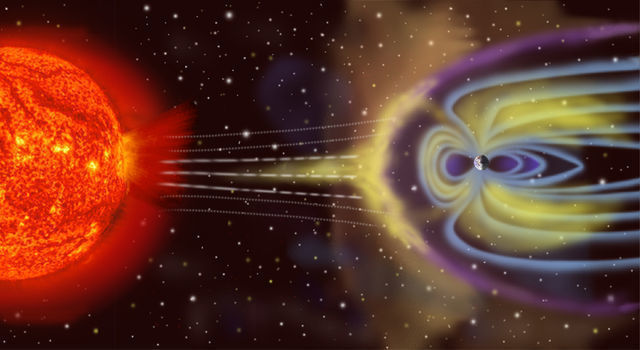
Die Sonne sendet ständig einen als Sonnenwind (engl. solar wind) bezeichneten Strom von sehr schnellen geladenen Teilchen aus. Der Teil des Sonnenwindes, der die Erde erreicht, verformt das Magnetfeld der Erde (Bild 13.33). Das Erdmagnetfeld hält den Teilchenschauer zum größten Teil von der Erde ab. Bei langen Reisen außerhalb der Magnetosphäre (zum Beispiel bei einer Marsmission) ist der Schutz der Besatzung vor der Strahlenbelastung durch den Sonnenwind ein schwieriges Problem.
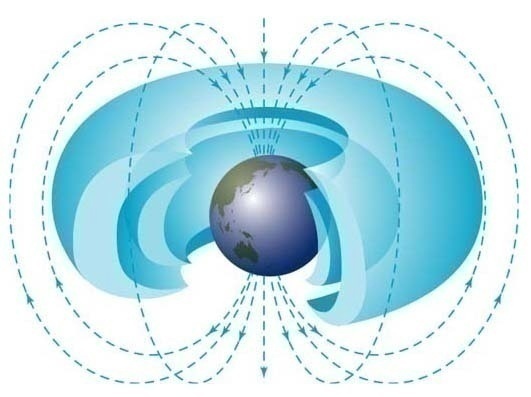
Ein Teil der geladenen Teilchen aus dem Sonnenwind wird zwischen den Magnetpolen der Erde wie in einer magnetischen Flasche gefangen. Diese wulstförmigen Bereiche um die Erde werden als Van-Allen-Strahlungsgürtel bezeichnet (Bild 13.34).
An den Polen kommen diese Teilchen der Erde dabei so nahe, dass sie dort mit Luftmolekülen aus der Atmosphäre zusammenstoßen und die als Polarlicht bekannte Leuchterscheinung hervorrufen (Nordpol: Aurora borealis; Südpol: Aurora australis).