13.2 Geladene Teilchen in Magnetfeldern
Im Bild 13.19 siehst du das Schnellboot Yamato-1. Das Besondere an diesem Schiff: Der Antrieb besitzt keine mechanischen Teile!
In diesem Kapitel erfährst du unter anderem, welche Kraft auf ein geladenes Teilchen in einem Magnetfeld wirkt, wie Einheit und Größe des Magnetfeldes definiert werden und wie ein Antrieb ohne bewegliche Teile gebaut werden kann.
13.2.1 Kraft auf eine Ladung in Magnetfeldern
In einem elektrischen Feld wirkt auf eine Ladung \(q\) die Coulombkraft. Sie zeigt für positive Ladungen in Richtung der elektrischen Feldlinien und hat den Betrag \(F_C = E\cdot q\). Die Coulombkraft wirkt unabhängig vom Bewegungszustand der Ladung.
Im Gegensatz dazu übt ein Magnetfeld eine Kraft nur auf bewegte Ladungen aus. Diese magnetische Kraft auf eine Ladung nennen wir (zu Ehren von Hendrik Antoon Lorentz und zur Unterscheidung der Coulombkraft \(F_C\) durch das elektrische Feld) Lorentzkraft \(F_L\) (engl. forentz force).
Experimente zeigen, dass die Lorentzkraft folgende Eigenschaften hat (Bild 13.20):
Die Lorentzkraft steigt proportional mit der Größe der Ladung \(q\), der Geschwindigkeit der Ladung \(v\) und Größe des Magnetfeldes \(B\).
Die Lorentzkraft steht immer im rechten Winkel sowohl zur Geschwindigkeitsrichtung \(\vec{v}\) der Ladung als auch zur Magnetfeldrichtung \(\vec{B}\).
Die Lorentzkraft ist am größten, wenn Magnetfeld und Geschwindigkeitsrichtung im rechten Winkel aufeinander stehen. Zwischen 0° und 90° ändert sich die Kraft mit dem Sinus des Winkels zwischen Magnetfeld und Geschwindigkeitsrichtung. Bewegt sich die Ladung in Richtung des magnetischen Feldes (parallel oder anti-parallel), ist die Lorentzkraft null.
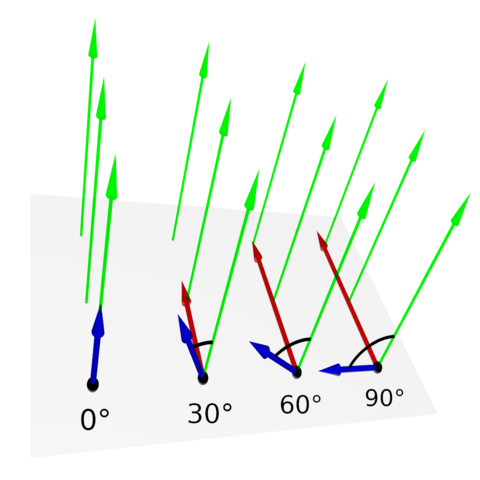
Bild 13.20: Kraft (rot) auf eine positive Ladung in einem Magnetfeld (grün) für unterschiedliche Geschwindigkeitsrichtungen (blau) der bewegten Ladung
Aus diesen Eigenschaften bietet es sich an, für die mathematische Beschreibung der Lorentzkraft auf eine Ladung das Kreuzprodukt zu verwenden.
| \[\begin{equation} \vec{F}_L = q\cdot \vec{v}\times\vec{B} \tag{13.1} \end{equation}\] |
In dieser Gleichung bedeutet:
- \(\vec{F}_L\), die Kraft auf geladenes Teilchen (in \(\mathrm{N}\))
- \(q\), die elektrische Ladung des Teilchens (in \(\mathrm{C}\))
- \(\vec{v}\), die Geschwindigkeit des Teilchens (in \(\mathrm{m/s}\))
- \(\vec{B}\), die magnetische Flussdichte des Feldes am Ort des Teilchens (in \(\mathrm{T}\))
Dieselbe Gleichung ohne Vektoren lautet:
\[\begin{equation} F_L = q\cdot v\cdot B\cdot \sin(\alpha) \tag{13.2} \end{equation}\]
Dabei ist \(\alpha\) der Winkel zwischen Magnetfeldrichtung und Geschwindigkeitsrichtung des Teilchens.
13.2.2 Merkregel für die Richtung der Lorentzkraft
Die UVW-Regel (Ursache-Vermittler-Wirkung) hilft dir, die Richtung der Lorentzkraft zu bestimmen. Um die Kraftrichtung für eine positive Ladung zu bestimmen, verwendest du deine rechte Hand. Beginne – so wie beim Zählen mit den Fingern – mit dem Daumen:
- Finger (Daumen) zeigt in die Geschwindigkeitsrichtung \(\vec{v}\) (Ursache)
- Finger (Zeigefinger) zeigt in die Magnetfeldrichtung \(\vec{B}\) (Vermittler)
- Finger (Mittelfinger) zeigt in die Richtung der Lorentzkraft \(\vec{F}_L\) (Wirkung)
Stehen die Geschwindigkeitsrichtung und das Magnetfeld im rechten Winkel zueinander, bilden deine Finger der rechten Hand ein Dreibein wie in Bild 13.21 (rechts). Die Regel funktioniert aber auch, wenn Magnetfeldrichtung und Geschwindigkeitsrichtung einen Winkel ungleich \(90^\circ\) einschließen. Achte nur darauf, dass der Mittelfinger immer im rechten Winkel zu deiner Handfläche abgespreizt wird.
Für negative Ladungen gibt es zwei mögliche Merkhilfen:
Du bestimmst die Richtung der Lorentzkraft so, als wäre es eine positive Ladung. Hast du die Richtung ermittelt, nimm die entgegengesetzte Richtung – das negative Vorzeichen der negativen Ladung kehrt die Kraftrichtung um.
Statt der rechten Hand verwendest du für die Bestimmung der Lorentzkraftrichtung bei negativer Ladung die linke Hand und wendest die UVW-Regel wie gewohnt an (Bild 13.21 (links)).
Verwende die Merkhilfe, die dir besser gefällt, aber vermische sie nicht!
13.2.3 Magnetfeld B
Sowohl bei der Definition der Feldstärke des Gravitationsfeldes als auch der Feldstärke des elektrischen Feldes sind wir so vorgegangen, dass wir die Feldkraft auf einen Einheitskörper bezogen haben. Also konkret: die Gravitationskraft pro Einheitsmasse beziehungsweise die Coulombkraft pro Einheitsladung. Soweit wir wissen, gibt es so etwas wie einen magnetischen Einheitskörper in der Natur nicht. Daher müssen wir uns für die Definition des Magnetfeldes etwas anderes einfallen lassen.
Für die Definition des Magnetfeldes \(B\) können wir die Lorentzkraft auf eine Testladung verwenden. Durch Umformen erhalten wir:
| \[\begin{equation} B = \frac{F_B}{q\cdot v} \tag{13.3} \end{equation}\] |
In der Gleichung bedeuten:
- \(F_B\), die Lorentzkraft (in \(\mathrm{N}\))
- \(v\), die Geschwindigkeit der Testladung (in \(\mathrm{m/s}\))
- \(q\), die Größe der Testladung (in \(\mathrm{C}\))
Die Stärke des Magnetfeldes \(B\) wird aus historischen Gründen nicht als magnetische Feldstärke, sondern als magnetische Flussdichte (engl. magnetic flux density) oder als magnetische Induktion (engl. magnetic induction) bezeichnet.
13.2.4 Einheit der magnetischen Flussdichte
Die Einheit folgt direkt aus der Definition der magnetischen Flussdichte:
\[ [B] = \frac{[F_B]}{[q]\cdot[v]} = 1\;\frac{\mathrm{N}}{\mathrm{C}\cdot\mathrm{m/s}} = 1\;\frac{\mathrm{N\cdot s}}{\mathrm{C}\cdot\mathrm{m}} = 1\;\mathrm{T} \]
Die Einheit „Newton-Sekunde pro Coulomb-Meter“ wird – zu Ehren des Erfinders Nikola Tesla – ein Tesla (\(\mathrm{T}\)) genannt.
Das Tesla ist eine große Einheit. Zum Vergleich: Das Erdmagnetfeld in Mitteleuropa beträgt nur rund \(50\;\mathrm{\mu T}\) (millionstel Tesla), Haftmagnete für Pinnwände erreichen einige hundertstel Tesla und die stärksten Permanentmagnete haben Flussdichten von bis zu \(0{,}4\;\mathrm{T}\).
13.2.5 Elektromagnetische Kraft
Bisher sind wir immer von einem elektrischen oder einem magnetischen Feld ausgegangen. Sind beide Felder vorhanden, ist die Kraft auf eine Ladung \(q\) die Vektorsumme (Superposition) von Coulombkraft und Lorentzkraft.
\[ \begin{aligned} \vec{F} = {} & \vec{F}_C + \vec{F}_L \\ \vec{F} = {} & q\cdot \vec{E} + q\cdot \vec{v}\times\vec{B} \\ \end{aligned} \]
Oder nach Herausheben von \(q\):
| \[\begin{equation} \vec{F} = q\cdot (\vec{E} + \vec{v}\times\vec{B}) \tag{13.4} \end{equation}\] |
Dieser Ausdruck beschreibt ganz allgemein die elektromagnetische Kraft (engl. electromagnetic force) auf eine Ladung.
13.2.6 Hall-Effekt
Ein Hall-Plättchen ist ein Halbleiter-Plättchen, das in Längsrichtung von einem konstanten Strom durchflossen wird. Befindet sich das Hall-Plättchen in einem Magnetfeld und zeigt die Feldrichtung aus der Bildebene (Bild 13.22), erfahren die Elektronen eine Lorentzkraft durch die Magnetfeldkomponente normal zu dem Plättchen. Bewegen sich die Elektronen von rechts nach links und zeigen die Magnetfeldlinien aus der Bildebene heraus, werden die Elektronen nach der UVW-Regel nach unten abgelenkt. An der Unterseite des Plättchens kommt es dadurch zu einem Elektronenüberschuss und an der Oberseite zu einem Elektronenmangel (Hall-Effekt (engl. hall effect)). Das entspricht einer Potenzialdifferenz, die als elektrische Spannung zwischen den beiden Kontakten oben und unten messbar ist – die sogenannte Hall-Spannung (engl. hall voltage).
Ein Hall-Plättchen misst immer nur die Magnetfeldkomponente im rechten Winkel zur Oberfläche des Plättchens. Eine Hall-Sonde besteht daher aus drei paarweise im rechten Winkel angeordneten Hall-Plättchen. Aus der Vektorsumme aller drei Hall-Spannungen kann die Größe und Richtung des Magnetfeldes an einer Stelle im Feld bestimmt werden.
Links:
- WebApp: Hall Effekt
13.2.7 Magnetohydrodynamik
Befindet sich eine leitende Flüssigkeit (zum Beispiel Meerwasser oder Blut) in einem Magnetfeld und kommt es durch Anlegen einer elektrischen Spannung zu einem Stromfluss, werden alle geladenen Teilchen durch die Lorentzkraft quer zur Strömungsrichtung beschleunigt (Bild 13.23). Dabei spielt das Vorzeichen der geladenen Teilchen keine Rolle. Da sich positive und negativ geladene Teilchen bei einem Stromfluss in entgegengesetzte Richtungen bewegen, werden sie durch die Lorentzkraft in dieselbe Richtung abgelenkt! Alle ungeladenen Teilchen werden durch Reibung mit den geladenen Teilchen mitbewegt.
Dieses Prinzip der Magnetohydrodynamik (MHD) (engl. magnetohydrodynamics) kann als Schiffsantrieb oder als Pumpe ohne mechanische Teile verwendet werden. Mit der Umkehrung des Prinzips lässt sich ein elektrischer Generator ohne mechanische Teile bauen. Auch wenn sich der magnetohydrodynamische Antrieb für Schiffe und der Generator zur elektrischen Energiegewinnung als zu unwirtschaftlich herausgestellt haben, gibt es weitere Anwendungen dieses Verfahrens.
Links:
- Bauanleitung: Boot mit magnetohydrodynamischen Antrieb





