12.3 Elektrostatisches Feld
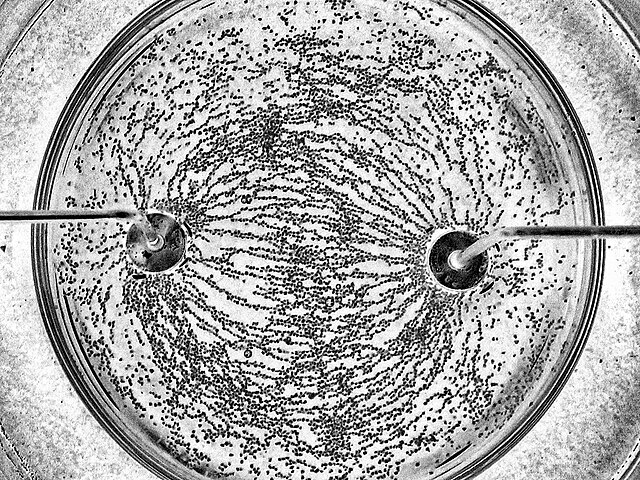
Verteilst du Grießkörner auf eine Schicht Rizinusöl zwischen zwei Metallkontakten und lädst einen davon mit einem Bandgenerator, während der andere Kontakt geerdet wird, werden die Grießkörner elektrisch polarisiert. Sie fügen sich zu langen Ketten zusammen (Bild 12.20). Der Grund dafür ist, dass die ungleichnamigen Enden der Grießkorn-Dipole einander anziehen und versuchen, einander möglichst nahezukommen.
Das Bild hat Ähnlichkeiten mit den Feldlinienbildern des Gravitationsfeldes. In diesem Kapitel übertragen wir den Feldbegriff, wie wir ihn bei der Schwerkraft schon kennengelernt haben, auf die elektrische Kraft. Das durch elektrische Ladungen verursachte Feld nennen wir elektrisches Feld (engl. electric field). Als elektrostatisches Feld bezeichnen wir elektrische Felder, die sich mit der Zeit nicht ändern. In diesem Kapitel wirst du außerdem das Feld einiger besonderer Ladungsanordnungen kennenlernen.
Links:
- Video: Influenzmaschine und Grießkörner in Rizinusöl
- Video: Elektrische Felder (durch Grießkörner sichtbar gemacht)
12.3.1 Feldstärke des elektrischen Feldes
Legst du einen Probekörper mit kleiner positiver Ladung an einen beliebigen Raumpunkt, kannst du dort die elektrische Kraft durch andere Ladungen messen. Damit ist die Voraussetzung für ein Vektorfeld erfüllt. Da jede Ladung das Feld verändert, muss eine Probeladung möglichst klein im Verhältniss zu den felderzeugenden Ladungen gewählt werden, damit das Feld damit möglichst unverfälscht gemessen werden kann. Liest du im Text die Begriffe „Probeladung“ oder „geladener Testkörper“, ist damit immer ein Körper mit so einer kleinen Ladung gemeint.
Wie schon bei der Definition der Feldstärke im Gravitationsfeld soll auch im elektrischen Feld der Feldvektor unabhängig von der Ladung des jeweiligen Testkörpers sein. Nach Messung der Kraft auf eine Probeladung erhältst du die elektrische Feldstärke \(E\) (engl. electric field strength) als Quotient aus Coulombkraft \(F_C\) und Ladung \(q\) des Testkörpers.
| \[\begin{equation} \vec{E}=\frac{\vec{F}_C}{q} \tag{12.6} \end{equation}\] |
Durch Einsetzen in die Definitionsgleichung erhältst du für die Einheit der elektrischen Feldstärke:
\[ [E] = \frac{[F]}{[q]} = 1\;\frac{\text{N}}{\text{C}} \]
Die Einheit „Newton pro Coulomb“ spiegelt wider, dass es sich bei der elektrischen Feldstärke um die Kraft pro Einheitsladung (\(+1\text{C}\)) handelt.
Umgekehrt gilt: Befindet sich eine Ladung \(q\) in einem elektrischen Feld mit der Feldstärke \(E\), erfährt die Ladung eine Kraft der Größe
\[\begin{equation} \vec{F} = q\cdot \vec{E} \tag{12.7} \end{equation}\]
Links:
- WebApp: Ladungen und Felder
12.3.2 Elektrische Feldstärke einer Punktladung
Wenden wir die Definition der elektrischen Feldstärke auf das konkrete Beispiel einer punktförmigen Ladung an. Die elektrische Kraft \(F\) einer Testladung \(q\) im Feld einer Punktladung \(Q\) ist durch das Coulombsche Gesetz (Gleichung (12.2)) beschrieben:
\[ F=k\cdot{\frac {q\cdot Q}{r^{2}}} \]
Setzen wir in Definitionsgleichung (12.6) der Feldstärke ein, erhalten wir das Ergebnis:
\[\begin{align} E = {} & F\cdot\frac{1}{q} \notag \\ E = {} & k\cdot{\frac {q\cdot Q}{r^{2}}} \cdot \frac{1}{q} \notag \\ E = {} & k\cdot{\frac {Q}{r^{2}}} \tag{12.8} \\ \end{align}\]
12.3.3 Feldliniendarstellung des elektrischen Feldes
Elektrische Vektorfelder werden oft durch Feldlinien dargestellt (Bild 12.21).
Aus dem Feldlinienbild kannst du folgende Eigenschaften des elektrischen Feldes ablesen:
die Richtung des Kraftvektors (Feldstärkevektors) in einem beliebigen Punkt des Feldes entspricht der Richtung der Tangente an die Feldlinie an dieser Stelle.
Für positive Ladungen wirkt die elektrische Kraft in Feldlinienrichtung (\(q_1\), \(q_2\) in Bild 12.21), für negative Ladungen gegen die Feldlinienrichtung (\(q_3\) in Bild 12.21).
Größe der Kraft (Feldstärke) in einem beliebigen Punkt des Feldes. (Die (relative) Dichte der Feldlinien ist ein Maß für die Stärke des Feldes im jeweiligen Bereich.) Im Feldlinienbild 12.21 liegen die Feldlinien in der Umgebung von Testladung \(q_1\) dichter beisammen als in der Umgebung der Testladung \(q_2\). Sind beide Ladungen gleich groß, ist die Kraft auf die Ladung \(q_1\) größer als auf \(q_2\).
Eigentlich gibt es unendlich viele Feldlinien in einem Feld, die beliebig dicht beieinanderliegen. Die Anzahl der tatsächlich gezeichneten Feldlinien wird so gewählt, dass die Eigenschaften des Feldes gut erkennbar sind. Daher ist die Dichte der Feldlinien in einem Feldlinienbild kein absolutes Maß für die Feldstärke, sondern erlaubt es nur, die Feldstärken relativ zueinander innerhalb eines Feldlinienbildes abzuschätzen.
In jedem Punkt des Feldes gibt es eine eindeutige Kraft. Daher können sich Feldlinien auch nicht kreuzen. Am Kreuzungspunkt gäbe es sonst zwei Kraftrichtungen.
12.3.4 Feld einer punktförmigen Ladung
Für die Feldstärke einer Punktladung haben wir den Ausdruck
\[ E = k\cdot\frac{Q}{r^{2}} \]
erhalten. Wie du sehen kannst, nimmt sie mit dem Quadrat des Abstandes ab.
Alle Feldlinien einer einzelnen punktförmigen oder kugelsymmetrischen elektrischen Ladung verlaufen geradlinig durch die Ladung (Bild 12.22), ein sogenanntes Radialfeld. Für die Messung der Kraft an einer Stelle in einem elektrischen Feld wird – definitionsgemäß – stets ein positiv geladener Probekörper verwendet. Er wird von anderen positiven Ladungen abgestoßen und von negativen Ladungen angezogen. Daraus ergibt sich die Feldlinienrichtung im elektrischen Feld.
| Die elektrischen Feldlinien entspringen an positiven Ladungen und enden an negativen Ladungen. |
12.3.5 Feld zweier punktförmiger Ladungen
In Bild 12.23 siehst du das Feld von zwei gegengleich geladenen Punktladungen. Dieses Feld wird als elektrisches Dipolfeld (engl. electric dipole field) bezeichnet.
In Bild 12.24 ist das Feldlinienbild von zwei gleich geladenen Punktladungen zu sehen.
Beachte den Bereich um den Mittelpunkt zwischen den beiden Ladungen. Hier gibt es einen kräftefreien Punkt (engl. point of zero net force), in dem sich alle Kräfte aufheben. In diesem Punkt verschwindet die Feldstärke. Die Verbindungslinie zwischen den beiden Ladungen trägt je eine Feldlinie, die von der Ladung zum Mittelpunkt verläuft, und zwar mit entgegengesetzter Richtung. Eine Feldlinie kann immer nur eine Richtung haben!
12.3.6 Elektrisches Feld zweier gegengleich geladener paralleler Platten
In Bild 12.25 siehst du das Feldlinienbild von zwei gegengleich geladener paralleler Platten. Eine solche Anordnung findest du zum Beispiel bei einem Plattenkondensator.
Beachte den Feldbereich in der Mitte des Kondensators. In diesem Bereich verlaufen die Feldlinien (fast) alle parallel und ihre Dichte ist überall (fast) gleich. Das bedeutet, dass die Feldstärke in diesem Bereich überall gleich ist. Es handelt sich um einen homogenen Feldbereich. Dort sind die Verhältnisse besonders einfach. Die Feldstärke beträgt dort (ohne Herleitung)
\[\begin{equation} E= 4\cdot\pi\cdot k\cdot\frac{Q}{A}= \frac{Q}{\varepsilon_0\cdot A} \tag{12.9} \end{equation}\]
Die Fläche \(A\) entspricht der Fläche einer Kondensatorplatten(seite) und \(Q\) entspricht der auf dem Kondensator befindlichen Gesamtladung.
12.3.7 Geländedarstellung des elektrischen Feldes
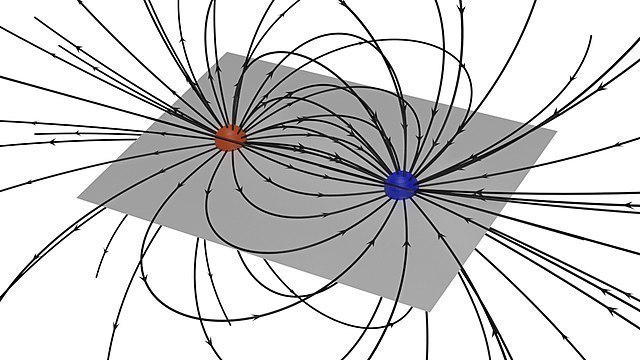
Das elektrische Feld ist dreidimensional und erfüllt den Raum. Um die wesentlichen Eigenschaften eines Feldes zu zeigen, ist in vielen Fällen ein zweidimensionaler Schnitt durch das Feld ausreichend. Das elektrische Dipolfeld in Bild 12.23 erhältst du, wenn du den Schnitt entlang der grauen Ebene, die durch die Mittelpunkte beider Ladungen verläuft, im Bild 12.26 wählst.
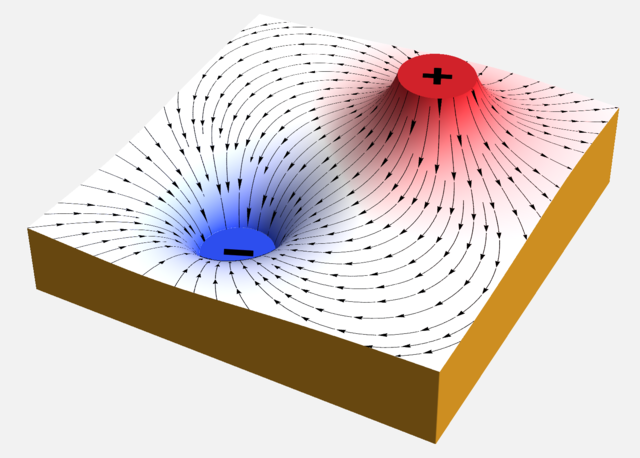
So ein zweidimensionaler Schnitt eines elektrostatischen Feldes lässt sich auch in Form eines Geländemodells veranschaulichen. Das Geländemodell des elektrischen Dipolfeldes siehst du in Bild 12.27.
Das Verhalten einer positiven Testladung kannst du dir als Verhalten einer Kugel in diesem Gelände vorstellen. Legst du sie in der Nähe der positiven Ladung ins Gelände (Berg) und lässt sie los, wird sie, dem Gefälle folgend, in Richtung der negativen Ladung (Tal) rollen. In Analogie zu Wasser werden die positiven Ladungen daher auch Quellen und die negativen Ladungen Senken des elektrischen Feldes genannt.
12.3.8 Elektrischer Fluss
Der Größe des elektrischen Flusses (engl. electric flux) liegt eine sehr anschauliche Vorstellung zugrunde. Du kannst ihn dir als „Maß für die Anzahl der Feldlinien durch eine Fläche“ vorstellen.
Im Bild 12.28 siehst du als einfaches Beispiel den elektrischen Fluss durch zwei identische Flächen mit unterschiedlicher Ausrichtung in einem homogenen Feld. Der elektrische Fluss durch die linke Fläche ist kleiner als durch die rechte Fläche.
Diese anschauliche Vorstellung kann für die mathematische Definition des elektrischen Flusses aber nicht verwendet werden, da die Anzahl aller Feldlinien immer unendlich ist.
Die elektrische Feldstärke ist ein Maß für die Stärke des Feldes und daher wird der elektrische Fluss als inneres Produkt von Feldstärke \(\vec{E}\) und dem Flächennormalvektor \(\vec{A}\) der Fläche definiert:
| \[\begin{equation} \Phi_E=\vec{E}\cdot\vec{A} \tag{12.10} \end{equation}\] |
Als Formelsymbol für den Fluss wird üblicherweise der griechische Großbuchstabe Phi verwendet. Der Index \(E\) drückt aus, dass es sich um den Fluss des elektrischen Feldes handelt.
Das Skalarprodukt ist am größten, wenn beide Vektoren in dieselbe Richtung zeigen (im Einklang mit Bild 12.28 rechts), es wird kleiner, je näher der Winkel bei 90 Grad liegt (im Einklang mit Bild 12.28 links) und wird schließlich null, wenn beide Vektoren normal zueinanderstehen – in Analogie zu unserer anschaulichen Vorstellung: Keine Feldlinie durchdringt mehr die Fläche. Ohne Vektoren kann der elektrische Fluss durch
\[ \Phi_E=E\cdot A\cdot\cos(\alpha) \]
ausgedrückt werden, wobei \(\alpha\) der Winkel zwischen Feldlinie und Flächennormale ist.
Formst du die Definitionsgleichung (12.10) des elektrischen Flusses um, erhältst du den Ausdruck:
\[ E = \frac{\Phi_E}{A} \]
Diesen Ausdruck kannst du dir als „Anzahl der Feldlinien durch die Einheitsfläche“ vorstellen. Je größer der Fluss, desto mehr Feldlinien durchdringen die Einheitsfläche und desto dichter liegen die Feldlinien. Deshalb wird die elektrische Feldstärke \(E\) auch als elektrische Flussdichte bezeichnet.
12.3.9 Elektrischer Fluss um eine Punktladung
In nicht homogenen Feldern, wo sich die elektrische Feldstärke von Punkt zu Punkt ändert, muss für die meisten Fälle die Integralrechnung für die Berechnung des elektrischen Flusses verwendet werden. Der elektrische Fluss durch eine Kugeloberfläche um eine Punktladung (Bild 12.29) ist eine der wenigen Ausnahmen.
Dadurch, dass sich die punktförmige Ladung im Mittelpunkt der Kugeloberfläche befindet (also überall gleich weit entfernt ist), steht der Feldstärkenvektor in jedem Punkt normal auf die Kugeloberfläche und hat überall dieselbe Länge.
Der elektrische Fluss ist in diesem speziellen Fall einfach das Produkt aus Feldstärke der Punktladung und der Kugeloberfläche:
\[\begin{align} \Phi_E = {} & E\cdot A \notag \\ \Phi_E = {} & \left(k\cdot\frac{Q}{r^2}\right)\cdot (4\pi \cdot r^{2}) \notag \\ \Phi_E = {} & k\cdot Q\cdot4\pi \notag \end{align}\]
Mit dem Zusammenhang von Coulomb-Konstante und elektrischer Feldkonstante (Gleichung (12.4)) lässt sich das Ergebnis noch einfacher ausdrücken:
\[\begin{align} \Phi_E = {} & k\cdot Q\cdot4\pi \notag \\ \Phi_E = {} & \frac {1}{4\pi\varepsilon_{0}} \cdot Q\cdot4\pi \notag \\ \Phi_E = {} & \frac {Q}{\varepsilon_{0}} \notag \\ \end{align}\]
Obwohl wir den elektrischen Fluss einer Punktladung nur durch eine Kugeloberfläche hergeleitet haben, kann gezeigt werden, dass dieses Ergebnis ganz allgemein für jede beliebige geschlossene Oberfläche um eine punktförmige Ladung gilt!
12.3.10 Elektrischer Fluss ohne eingeschlossene Ladung
Betrachten wir den Fall einer geschlossenen Oberfläche, innerhalb der sich keine einzige Ladung befindet (Bild 12.30).
Jede Feldlinie, die an einer Stelle der geschlossenen Oberfläche eintritt, verlässt sie an einer anderen Stelle. Daraus können wir schließen:
| Der elektrische Gesamtfluss durch eine geschlossene Oberfläche, die keine Ladung enthält, ist immer null (\(\Phi_E = 0\)). |
12.3.11 Anwendungsbeispiel: Feldstärke eines elektrischen Dipols
Ein elektrischer Dipol besteht aus zwei gleich großen Ladungen mit entgegengesetztem Vorzeichen. Der Abstand zwischen den Ladungen beträgt \(2a\). Finde einen Ausdruck für die elektrische Feldstärke \(E\) im Punkt \(P\), der sich gleich weit von beiden Ladungen entfernt befindet. Der Abstand \(r\) vom Dipol soll größer als der Abstand \(a\) sein (\(r \gg a\)).
Aus Symmetriegründen folgt, dass auf eine positive Testladung im Punkt \(P\) der Betrag der abstoßenden Kraft durch die positive Ladung \(q\) und der Betrag der anziehenden Kraft durch die negative Ladung \(-q\) gleich groß sind. Mit der Definition der elektrischen Feldstärke gilt für die Beträge:
\[ E_1 = E_2 = k \cdot \frac{q}{b^2} \]
Wenden wir den Satz des Pythagoras im rechtwinkeligen Dreieck 1 an, können wir das Hypotenusen-Quadrat durch die Summe der Katheten-Quadrate ersetzen und wir erhalten:
\[\begin{equation} E_1 = E_2 = k \cdot \frac{q}{r^2+a^2} \tag{12.11} \end{equation}\]
Für die Gesamtfeldstärke \(\vec{E}_\text{ges}\) müssen wir die Vektorsumme der beiden Feldstärken \(\vec{E}_1\) und \(\vec{E}_2\) bilden. In Bild 12.31 sehen wir, dass die x-Komponenten beider Feldstärken immer entgegengesetzt gleich groß sind und sich damit aufheben. Der Betrag der Gesamtfeldstärke \(E_\text{ges}\) ist somit die doppelte Länge der Ankathete im rechtwinkeligen Dreieck 2, die wir mithilfe des Kosinus ausdrücken können. Es gilt:
\[\begin{equation} \cos(\alpha) = \frac{a}{b} = \frac{a}{(r^2+a^2)^{1/2}} \tag{12.12} \end{equation}\]
Setzen wir die Ausdrücke (12.11) und (12.12) ein, erhalten wir für den Betrag der gesuchten Gesamtfeldstärke:
\[ \begin{aligned} E_\text{ges} = {} & 2\cdot E_1\cdot \cos(\alpha) \\ = {} & 2\cdot \left(k \cdot \frac{q}{r^2+a^2}\right)\cdot \left(\frac{a}{(r^2+a^2)^{1/2}}\right)\\ = {} & k \cdot \frac{2\cdot q\cdot a}{(r^2+a^2)^{3/2}}\\ \end{aligned} \]
Gehen wir davon aus, dass \(r\) viel größer als \(a\) ist (\(r \gg a\)), dann ist \(r^2\) noch viel größer als \(a^2\) und wir können den Betrag von \(a\) im Ausdruck vernachlässigen. Damit erhalten wir näherungsweise:
\[\begin{equation} E_\text{ges} \approx k \cdot \frac{2\cdot q\cdot a}{r^3} \tag{12.13} \end{equation}\]
Beim elektrischen Dipol nimmt die Feldstärke mit der Entfernung mit \(1/r^3\) ab und damit schneller als die Feldstärke einer elektrischen Punktladung, deren Feldstärke „nur“ mit \(1/r^2\) abnimmt. Das ist auch anschaulich einzusehen, da sich die Wirkungen von gleich großen positiven und negativen Ladungen aufheben, erscheint ein Dipol aus großer Entfernung als elektrisch neutral, wie es auch bei Atomen der Fall ist.