13.4 Magnetfelder durch Stromfluss
Werden starke Magnetfelder benötigt, kommen immer Elektromagneten zum Einsatz, wie der Elektromagnet für ein Zyklotron in Bild 13.35.
In diesem Kapitel geht es um das magnetische Feld, das durch einen stromdurchflossenen Leiter entsteht, und den Elektromagneten.
13.4.1 Ørsted Experiment
Im Jahr 1820 veröffentlichte Hans Christian Ørsted seine Entdeckung, dass eine Kompassnadel durch einen nahegelegenen elektrischen Strom von der Nordrichtung abgelenkt wird und bestätigte damit eine direkte Beziehung zwischen Elektrizität und Magnetismus.
Dieser Effekt kann durch die Versuchsanordnung in Bild 13.36 gezeigt werden (Ørsted Experiment). Ein Kabel wird parallel zu einer Kompassnadel ausgerichtet. Werden die Enden mit den Kontakten einer Batterie verbunden, fließt elektrischer Strom durch das Kabel und die Kompassnadel weicht von ihrer ursprünglichen Richtung ab. Die zweite Kompassnadel (links unten im Bild) ist so weit von dem Strom führenden Kabel entfernt, dass sie nicht beeinflusst wird und weiterhin in Richtung des geografischen Nordpols zeigt.
Je größer der Strom, desto stärker weicht die Nadel von ihrer ursprünglichen Richtung ab, bis sie schließlich im rechten Winkel zu dem Leiter steht. Ein Umdrehen der Stromrichtung bewirkt eine Abweichung der Nadel in die entgegengesetzte Richtung.
Link:
13.4.2 Magnetfeld eines geraden, stromdurchflossenen Leiters
Streust du Eisenfeilspäne um einen geraden stromdurchflossenen Leiter, erhältst du das Bild 13.37.
Da sich Eisenfeilspäne entlang der magnetischen Feldlinien anordnen, lässt sich das Magnetfeld um einen geraden elektrischen Leiter mithilfe von konzentrischen Kreisen (Kreisen mit gleichem Mittelpunkt) um den Leiter beschreiben. Diese liegen in Normalebenen zum Leiter. Um auch die Orientierung der Magnetfeldlinien zu bestimmen, untersuchen wir den Raum um den Leiter mithilfe einer Magnetnadel. In Bild 13.38 siehst du das Magnetfeld B eines stromdurchflossenen Leiters, wenn die technische Stromrichtung zu dir zeigt – also aus der Bildebene. Das wird in nachfolgenden Bildern durch einen \(\odot\) angedeutet (du siehst von vorn auf den Pfeil, also auf die Pfeilspitze), andernfalls wird ein \(\otimes\) gezeichnet (du siehst von hinten auf den Pfeil, also auf die gekreuzte Befiederung).
Im Gegensatz zu allen bisherigen Magnetfeldern hast du es hier mit einem Magnetfeld ohne Magnetpole zu tun!
Links:
- WebApp: Versuch Eisenfeilspäne
- WebApp: Magnetfeld eines geraden Leiters
13.4.3 Rechte-Faust-Regel für einen stromdurchflossenen Leiter
Die Richtung des Magnetfeldes eines geraden Leiters merkst du dir am einfachsten mit der Rechten-Faust-Regel (Korkenzieher-Regel). Umfasst du den Leiter mit deiner rechten Hand, sodass der ausgestreckte Daumen in Richtung der technischen Stromrichtung zeigt, weisen dir die restlichen Finger die Richtung der magnetischen B-Feldlinien (Bild 13.39).
13.4.4 Formel für das Magnetfeld eines geraden stromdurchflossenen Leiters
Die Stärke des magnetischen Feldes hängt nicht nur von der Stromstärke, sondern auch von der Entfernung vom Leiter ab – sie nimmt mit der Entfernung ab. Das B-Feld eines (mathematisch unendlich) langen geraden Leiters lässt sich durch die folgende Formel beschreiben:
\[\begin{equation} B = \frac{\mu_0}{2\cdot\pi} \cdot \frac{I}{r} \tag{13.8} \end{equation}\]
In dieser Formel bedeuten:
- \(B\), die magnetische Flussdichte (in \(\mathrm{T}\))
- \(I\), die elektrische Stromstärke (in \(\mathrm{C/s}\))
- \(r\), der radiale Abstand zum Leiter (in \(\mathrm{m}\))
- \(\mu_0\), die magnetische Feldkonstante (\(1.26\cdot 10^{-6}\;\mathrm{N/A^2}\))
Anders als das kugelsymmetrische elektrische Feld einer einzelnen Ladung, welches mit dem Quadrat des Abstands abnimmt, ist das magnetische Feld eines geraden Leiters zylindersymmetrisch und nimmt „nur“ mit linear mit der Entfernung \(r\) vom Draht ab.
Die Formel für das Magnetfeld eines geraden stromdurchflossenen Leiters lässt sich aus dem Biot-Savart-Gesetz herleiten, welches das Magnetfeld bewegter Ladungen beschreibt.
13.4.5 Magnetfeld eines ringförmigen, stromdurchflossenen Leiters
Biegst du den stromdurchflossenen Leiter zu einem Ring, erhältst du das Magnetfeld in Bild 13.40. Die technische Stromrichtung verläuft links aus der Bildebene und rechts in sie hinein. Die Richtung der Magnetfeldlinien ergibt sich wieder aus der Rechten-Faust-Regel, wenn du dir vorstellst, mit deiner rechten Hand in den Ring hineinzugreifen.
Im Gegensatz zu einem geraden Leiter hat diese Anordnung erkennbare Pole – oben der magnetische Nordpol und unten der magnetische Südpol. Ein Strom führender Ring ist also ein magnetischer Dipol (engl. magentic dipol)!
13.4.6 Helmholtz Spule
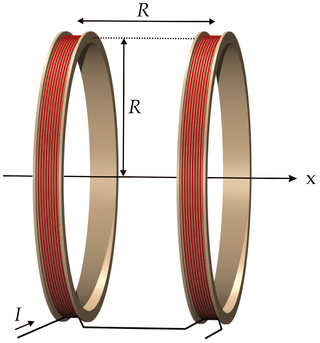
Die Anordnung in Bild 13.41, bei der zwei Spulen mit Radius \(R\) sich im Abstand \(R\) befinden, wird Helmholtz-Spule (engl. Helmholtz coil) genannt. Der Name geht auf Hermann von Helmholtz zurück. Eigentlich sind es zwei Spulen. Da es sich aber um zwei verbundene Spulen handelt, wird nur von der Helmholtz Spule (Einzahl) gesprochen.
Werden beiden Spulen gleichsinnig von Strom durchflossen, entsteht zwischen den beiden Spulen ein homogenes Feld (Bild 13.42). Es handelt sich dabei um die einfachste Spulenanordnung, mit der ein homogenes Magnetfeld (zwischen den Spulen) erzeugt werden kann.
13.4.7 Magnetfeld einer stromdurchflossenen Spule
Wickeln wir den stromdurchflossenen Leiter zu einer zylinderförmigen Spule, erhalten wir ein Magnetfeld, wie es in Bild 13.43 zu sehen ist.
Wickeln wir den Leiter ganz eng, erhalten wir eine dicht gewickelte Zylinderspule. Das Feld dieser Spule ist im Außenbereich von dem Feld eines Stabmagneten nicht mehr zu unterscheiden (Bild 13.44).
Im Gegensatz zu einem Stabmagneten kann die Polung einer Spule einfach durch Umkehren der Stromrichtung geändert werden.
Links:
- WebApp: Magnetfeld einer Spule
13.4.8 Magnetfeld einer sehr langen stromdurchflossenen Spule
Je länger die gewickelte Spule, desto homogener wird das Feld im Inneren der Spule (Bild 13.45).
Das homogene Magnetfeld im Inneren einer langen zylinderförmigen Spule lässt sich durch die folgende Gleichung beschreiben:
\[\begin{equation} B=\mu_0 \cdot \frac{N}{l}\cdot I \tag{13.9} \end{equation}\]
In dieser Formel bedeuten:
- \(B\), die magnetische Flussdichte (in \(\mathrm{T}\))
- \(\mu_0\), die magnetische Feldkonstante (\(1.26\cdot 10^{-6}\;\mathrm{N/A^2}\))
- \(N\), die Anzahl der Wicklungen (dimensionslose Zahl)
- \(l\), die Länge der Zylinderspule (in \(\mathrm{m}\))
- \(I\), die elektrische Stromstärke (in \(\mathrm{C/s}\))
Die Größe des B-Feldes nimmt also linear mit der Anzahl der Wicklungen und linear mit der Stromstärke zu.
Ein homogenes Feld einer langen Spule ist die magnetische Analogie zum elektrischen homogenen Feld eines Kondensators.
13.4.9 Magnetisches Dipolmoment
In Abschnitt Ausrichtung im Magnetfeld haben wir gezeigt, dass sich ein frei drehbarer magnetischer Dipol (zum Beispiel eine Kompassnadel) in einem äußeren Magnetfeld immer entlang der Feldlinien ausrichtet. Sein Nordpol zeigt dann in Feldlinienrichtung (Bild 13.46, a)
Für jede Drehung aus dieser Lage benötigst du Kraft und bei der Drehung verrichtest du Arbeit gegen die magnetischen Feldkräfte (Bild b). Das magnetische Moment eines Dipols \(\mu\) (engl. magnetic moment) entspricht der Arbeit, die bei der Drehung des Magneten in einem äußeren homogenen Magnetfeld der Stärke \(1\;\mathrm{T}\) gegen die Feldkräfte in eine rechtwinkelige Position zu den Feldlinien verrichtet werden muss. Ist für diese \(90^\circ\)-Drehung zum Beispiel die Arbeit \(1\;\mathrm{J}\) notwendig, dann ist das magnetische Moment des Dipols genau \(1\;\mathrm{J/T}\) („Joule pro Tesla“). Diese Arbeit ist dann als Energie im magnetischen Feld gespeichert.
Als Formelsymbol für das magnetische Dipolmoment wird meistens der griechische Kleinbuchstabe My (gesprochen „Mü“) verwendet. Vorsicht: Die magnetische Permeabilität hat dasselbe Formelsymbol! Manchmal wird daher für das magnetische Dipolmoment auch das Formelsymbol \(m\) verwendet.
Die meisten magnetischen Dipole in der Praxis bestehen aus einem Ringstrom, daher wird das magnetische Dipolmoment auch in der Einheit \(\mathrm{Am^2}\) („Ampere Quadratmeter“) angegeben.
13.4.10 Äquivalenz der Einheiten J/T und Am²
Da die Äquivalenz der Einheiten \(\mathrm{J/T}\) und \(\mathrm{Am^2}\) nicht auf den ersten Blick offensichtlich ist, möchten wir hier die Gleichheit zeigen.
Joule ist die Einheit der Arbeit. Aus der Definitionsgleichung der Arbeit folgt:
\[ 1\;\mathrm{J} = 1\;\mathrm{N}\cdot\mathrm{m} \]
Tesla ist die Einheit der magnetischen Flussdichte. Aus der Definitionsgleichung folgt:
\[ 1\;\mathrm{T} = 1\;\frac{\mathrm{N\cdot s}}{\mathrm{C}\cdot\mathrm{m}} \]
Die darin enthaltene Einheit der elektrischen Ladung ist über die elektrische Stromstärke definiert.
\[ 1\;\mathrm{C} = 1\;\mathrm{A}\cdot\mathrm{s} \]
Damit erhalten wir:
\[ 1\;\mathrm{T} = 1\;\frac{\mathrm{N}\cdot\mathrm{s}}{\mathrm{C}\cdot\mathrm{m}} = 1\;\frac{\mathrm{N}\cdot\cancel{\mathrm{s}}}{(\mathrm{A}\cdot\cancel{\mathrm{s}})\cdot\mathrm{m}} = 1\;\frac{\mathrm{N}}{\mathrm{A}\cdot\mathrm{m}} \]
Bilden wir davon den Kehrwert und setzen ein, sehen wir die Gleichheit der beiden Einheiten:
\[ 1\;\frac{\mathrm{J}}{\mathrm{T}} =1\;\mathrm{J}\cdot\frac{1}{\mathrm{T}} =1\;(\cancel{\mathrm{N}}\cdot\mathrm{m})\cdot\left(\frac{\mathrm{A}\cdot\mathrm{m}}{\cancel{\mathrm{N}}}\right) =1\;\mathrm{A}\cdot\mathrm{m}^2 \]
13.4.11 Drehmoment eines magnetischen Dipols
Befindet sich ein magnetischer Dipol (zum Beispiel eine Kompassnadel) in einem äußeren Magnetfeld und ist dieser nicht entlang der Feldlinien ausgerichtet, erfährt er eine Drehkraft (Drehmoment).
Diese Drehkraft lässt sich mithilfe des magnetischen Moments des Dipols beschreiben. Betrachten wir das magnetische Moment als einen Vektor, dessen Richtung vom Süd- zum Nordpol des Magneten zeigt, erhältst du das Drehmoment \(\vec{D}\) in einem homogenen Magnetfeld als Kreuzprodukt aus magnetischem Dipol-Moment-Vektor \(\vec{\mu}\) und magnetischer Flussdichte \(\vec{B}\) (Bild 13.47), oder:
\[\begin{equation} \vec{D} = \vec{\mu}\times\vec{B} \tag{13.10} \end{equation}\]
Die Stärke (und Richtung) dieser Drehkraft hängt nicht nur von der Größe des magnetischen Moments des Dipols ab, sondern auch von seiner Orientierung relativ zur Richtung des äußeren Magnetfeldes. Die Drehkraft ist maximal, wenn das magnetische Moment und die äußere Feldrichtung einen Winkel von \(90^\circ\) bilden. Der Betrag der Drehkraft ist in dieser Stellung das Produkt der Beträge
\[ D = \mu\cdot B \]
Aufgrund der geometrischen Eigenschaften des Kreuzprodukts lässt sich der Betrag des Drehmoments für beliebige Winkel \(\alpha\) mit der Formel
\[\begin{equation} D = \mu\cdot B\cdot\sin(\alpha) \tag{13.11} \end{equation}\]
berechnen. Setzen wir die Einheiten ein, erhalten wir die Einheit des Drehmoments.
\[ [D] = [\mu]\cdot[B] = 1\;\frac{\mathrm{J}}{\cancel{\mathrm{T}}} \cdot 1\;\cancel{\mathrm{T}} =1\;\mathrm{J} =1\;\mathrm{N}\cdot\mathrm{m} \]
13.4.12 Elektromagnet
Eine Spule mit einem Spulenkern (einem ferromagnetischen Material im Inneren der Spule) wird als Elektromagnet (engl. electromagnet) bezeichnet (Bild 13.48).

Bild 13.48: Einfacher Elektromagnet aus Batterie, Schaltdraht und Eisennagel
Die Elementarmagnete im ferromagnetischen Kernmaterial richten sich im Feld der Spule aus und verstärken es. Für eine Spule mit Eisenkern gilt:
\[\begin{equation} B = \mu_r \cdot B_0 \tag{13.12} \end{equation}\]
In dieser Formel bedeuten:
- \(B\), die magnetische Flussdichte der Spule mit Eisenkern (in \(\mathrm{T}\))
- \(B_0\), die magnetische Flussdichte der Spule ohne Eisenkern (in \(\mathrm{T}\))
- \(\mu_r\), die Permeabilitätszahl des Kernmaterials (dimensionslose Zahl)
Die Permeabilitätszahl ist eine materialabhängige Zahl, die angibt, um das Wievielfache das Magnetfeld durch einen Spulenkern aus diesem Material stärker wird. Für Eisen beträgt der Wert bei vollständiger Ausrichtung der Elementarmagnete rund \(10{.}000\). Das Feld der Spule wird also mit einem Eisenkern \(10{.}000\)-fach verstärkt!
13.4.13 Rechte-Faust-Regel für eine Spule
Die Rechte-Faust-Regel für einen stromdurchflossenen Leiter zeigt dir auch bei einer Spule verlässlich die Richtung der magnetischen Feldlinien an. Willst du nur die Polarität einer Spule wissen, ist die Rechte-Faust-Regel für eine Spule (engl. coil right hand rule) oft einfacher anzuwenden.
Umfasse die Spule so, dass die vier Finger deiner rechten Hand in die technische Stromrichtung zeigen (Bild 13.49). Der Daumen zeigt dann zum Nordpol der Spule.
13.4.14 Relais
Das Relais (ausgesprochen „Rö-lee“ Audio abspielen ) (engl. relay) ist ein elektromagnetischer Schalter. Wird der Steuerstromkreis geschlossen, wird die Spule zum Elektromagnet und schließt den Schalter des Laststromkreises (Bild 13.50).
Eine der ersten Anwendungen des Relais war die Telegrafie. Je länger ein Kabel, desto größer der elektrische Widerstand. Nach etwa \(30\;\mathrm{km}\) befand sich daher jeweils ein elektromagnetischer Schalter und eine Spannungsquelle, die das schwache Signal verstärkte. Der Name geht auf die Relaisstationen der Post zurück (von dem französischen Wort relais für „Pferdewechsel“). Vor der Erfindung der Telegrafie wurden eilige Nachrichten mit Pferdeboten verschickt. Bei solchen Stationen konnten die Reiter erschöpfte Pferde gegen frische tauschen.
Auch der erste Computer mit Rechenwerk und Speicher bestand aus Relais. 2.000 Stück davon verbaute Konrad Zuse 1941 in den Zuse Z3.
Links:
- Film: Funktion des Relais
13.4.15 Magnetfeld einer rotierenden geladenen Kugel
Als Nächstes betrachten wir das Magnetfeld einer rotierenden, geladenen Kugel. Drehen sich die Ladungen (in unserem Beispiel Elektronen) um ein Drehzentrum, entspricht das einem Ringstrom. Je weiter vom Drehzentrum entfernt, desto größer ist die Geschwindigkeit der Elektronen auf der Kugel und desto größer die Stromstärke in dieser Schicht. Das Magnetfeld lässt sich daher durch parallele Ringströme, deren Stromstärke in Richtung der Pole der Kugel abnimmt, annähern (Bild 13.51).
Das resultierende Magnetfeld aus all diesen Ringströmen siehst du im Bild 13.52. Da hauptsächlich die Ströme in Äquatornähe zum Feld beitragen, entspricht das Magnetfeld annähernd dem eines Stabmagneten.