13.5 Leiter in Magnetfeldern
13.5.1 Kraft auf einen Strom führenden Leiter in Magnetfeldern
Bisher haben wir die Lorentzkraft bei einzelnen bewegten Ladungen kennengelernt. Ein elektrischer Strom in einem Leiter besteht aus einer Vielzahl an Elektronen, die sich durch den Leiterquerschnitt bewegen. Auf ein stromdurchflossenes Leiterstück wirkt daher ebenfalls eine Lorentzkraft (Bild 13.53).
Richtung und Größe der Lorentzkraft auf ein Leiterstück wird durch ein Kreuzprodukt beschrieben. Die Gleichung lautet:
| \[\begin{equation} \vec{F}_L = I\cdot \vec{\ell}\times\vec{B} \tag{13.13} \end{equation}\] |
Beachte, dass die Stromstärke \(I\) zwar eine Richtung hat, mathematisch aber kein Vektor ist. Stattdessen ist die Länge des Leiterstücks ein Vektor. Der Richtungsvektor des Leiterstücks muss in die technische Stromrichtung zeigen, damit diese Gleichung stimmt.
Dieselbe Gleichung ohne Vektoren lautet:
\[\begin{equation} F_L = I\cdot \ell\cdot B\cdot \sin(\alpha) \tag{13.14} \end{equation}\]
Wobei \(\alpha\) der Winkel zwischen Magnetfeldrichtung \(\vec{B}\) und der gerichteten Länge \(\vec{\ell}\) des Leiterstücks ist. Die Richtung der Lorentzkraft steht immer im rechten Winkel zur Stromrichtung und zur Magnetfeldrichtung. Ist der Sinus von \(\alpha\) null – Stromrichtung und Magnetfeldrichtung parallel oder anti-parallel –, dann ist auch die Lorentzkraft null.
13.5.2 Herleitung der Lorentzkraft auf ein Leiterstück
Für die Herleitung gehen wir von einem geraden Stück Draht der Länge \(\ell\) aus, das mit der Stromstärke \(I\) durchflossen wird und sich in einem homogenen Magnetfeld \(B\) befindet (Bild 13.54).
Bewegen sich die Elektronen mit der konstanten Driftgeschwindigkeit \(v\) durch den Leiter, benötigen sie die Zeit
\[ t=\frac{s}{v}=\frac{\ell}{v} \]
um das Leiterstück zu durchqueren. Nach der Definition der Stromstärke gilt:
\[ \begin{aligned} I = {} & \frac{Q}{t}\qquad\Bigr\rvert\cdot t \\ I\cdot t = {} & Q\\ \end{aligned} \]
Setzen wir für die Zeit \(t\) ein, erhalten wir:
\[ \begin{aligned} Q = {} & I\cdot t \\ Q = {} & I\cdot\frac{\ell}{v} \\ \end{aligned} \]
Setzen wir diese Ladungsmenge in die Formel für die Lorentzkraft ein, erhalten wir den Ausdruck
\[ \begin{aligned} F_L = {} & Q\cdot v\cdot B \\ F_L = {} & I\cdot\frac{\ell}{v}\cdot v\cdot B \\ F_L = {} & I\cdot \ell\cdot B \\ \end{aligned} \]
für die Lorentzkraft auf ein Leiterstück.
13.5.3 Merkregel für die Richtung der Lorentzkraft auf ein Leiterstück
Wenn du bedenkst, dass die technische Stromrichtung und die Bewegungsrichtung der positiven Ladungsträger in dieselbe Richtung zeigen, ist es nicht schwer, die UVW-Regel (Ursache-Vermittler-Wirkung) für ein geladenes Teilchen auch für die Lorentzkraft auf ein Leiterstück anzuwenden (Bild 13.55): Wie für positive Ladungsträger verwendest du die rechte Hand. Beginne – so wie beim Zählen mit den Fingern – mit dem Daumen:
- Finger (Daumen) zeigt in die (technische) Stromrichtung \(I\) (Ursache)
- Finger (Zeigefinger) zeigt in die Magnetfeldrichtung \(B\) (Vermittler)
- Finger (Mittelfinger) zeigt in die Richtung der Lorentzkraft \(F_L\) (Wirkung)
Stehen die Stromrichtung und Magnetfeldrichtung im rechten Winkel zueinander, bilden die Finger deiner rechten Hand ein Dreibein wie in Bild 13.55. Du kannst die UVW-Regel auch dann verwenden, wenn Magnetfeldrichtung und Stromrichtung einen Winkel ungleich \(90^\circ\) einschließen. Achte nur darauf, dass der Mittelfinger immer im rechten Winkel zu deiner Handfläche abgespreizt wird.
13.5.4 Leiterschaukel-Experiment
Die Lorentzkraft auf ein Leiterstück kann zum Beispiel mit dem Leiterschaukel-Experiment gezeigt werden (Bild 13.56).
Eine lose aufgehängte Leiterschlaufe befindet sich im Feld eines Hufeisenmagnets. Wird der Strom eingeschaltet, kommt es zu einer deutlichen Bewegung der Leiterschlaufe. Befindet sich der Nordpol unten und zeigt die technische Stromrichtung von links nach rechts, bewegt sich der Leiter – im Einklang mit der UVW-Regel für ein Leiterstück – aus dem Hufeisenmagneten heraus. Wird die Stromrichtung oder die Polung des Hufeisenmagnets vertauscht, bewirkt die Lorentzkraft eine Bewegung der Leiterschlaufe in den Hufeisenmagneten hinein.
Im Bild 13.57 siehst du links das Magnetfeld des Hufeisenmagnets (braun) und das Magnetfeld des Leiters in blauer Farbe. Im Bereich (a) verlaufen die Feldlinien anti-parallel und das Magnetfeld wird geschwächt. Im Bereich (b) verlaufen die Feldlinien parallel und das Magnetfeld wird verstärkt. Auf der rechten Seite siehst du die Überlagerung (Superposition) beider Felder. Auch am Feldlinienbild kannst du die Richtung der Lorentzkraft erkennen: Sie erfolgt in Richtung abnehmender Feldliniendichte. Stell dir vor, die Feldlinien bestünden aus gespannten Gummifäden. Bewegt sich der Leiter nach links, entspannen sich die Gummischnüre.
Links:
- Video: Lorentzkraft auf Leiterstück
13.5.5 Messen der Lorentzkraft
In Bild 13.58 siehst du einen Versuchsaufbau, um die Lorentzkraft bei einem Leiterstück direkt zu messen.
Die Lorentzkraft auf die senkrechten Leiterstücke ist jeweils gleich groß und entgegengesetzt. Alle seitlichen Kräfte heben sich also auf – die Nettokraft ist null. Wird der Federkraftmesser vor dem Einschalten des Stroms auf null gestellt, kann die Lorentzkraft, die auf das waagrechte Leiterstück der Länge \(\ell\) wirkt, direkt auf der Skala abgelesen werden.
13.5.6 Kraft zwischen zwei parallelen Strom führenden Leitern
Die Lorentzkraft bewirkt eine Kraftwirkung zwischen zwei zueinander parallel angeordneten stromdurchflossenen Leitern. Fließen die Ströme anti-parallel, kommt es zu einer abstoßenden Kraft (Bild 13.59, links). Fließen die Ströme hingegen parallel, kommt es zu einer anziehenden Kraft (Bild 13.59, rechts).
Die Richtung der Kraftwirkung kannst du dir mithilfe eines Leiter-Elektrons des linken Drahtes im Magnetfeld des rechten Drahtes herleiten (Bild 13.60). Die Magnetfeldrichtung des rechten Leiters ist durch die Rechte-Faust-Regel festgelegt. Zeigt die technische Stromrichtung im linken Leiter nach unten, bewegen sich die negativen Leiter-Elektronen nach oben. Aus der Geschwindigkeitsrichtung des Elektrons und der Richtung des Magnetfeldes folgt nach der UVW-Regel für ein geladenes Teilchen eine abstoßende Kraft.
Auch am Feldlinienbild der beiden Leiter kannst du die abstoßende Wirkung bei anti-parallelen Strömen erkennen. Im Bereich zwischen den Leitern zeigen die Magnetfeldlinien in dieselbe Richtung und verstärken sich. Links und rechts neben den Drähten verlaufen die Magnetfeldlinien in entgegengesetzter Richtung. In diesem Bereich schwächen sich die Felder (Bild 13.61, oben). Darunter siehst du die Überlagerung (Superposition) beider Felder. Die Kraftwirkung erfolgt in Richtung abnehmender Feldstärke.
Im Falle von zwei parallel fließenden Strömen zeigen die Magnetfeldlinien im Zwischenraum der beiden Leiter in entgegengesetzter Richtung. Dort wird das Feld geschwächt (Bild 13.62, oben). Links und rechts neben den Drähten verlaufen die Feldlinien in dieselbe Richtung und verstärken das Feld. Darunter siehst du die Überlagerung beider Felder. Die Kraftwirkung erfolgt in Richtung abnehmender Feldstärke – hier kommt es zu einer anziehenden Wirkung.
Links:
- Video: Realexperiment - Parallele Ströme
- WebApp: Parallele Ströme
13.5.7 Ampèresches Kraftgesetz
Bisher haben wir nur die Kraftrichtung zwischen zwei parallelen Strom führenden Leitern betrachtet. Aber können wir die Größe der Kraft herleiten?
Die Kraft auf ein stromführendes Leiterstück der Länge \(\ell\) des zweiten Leiters im Magnetfeld des ersten Leiters ist (Bild 13.63):
\[ F_{2} = I_2\cdot \ell\cdot B_1 \]
Wir kennen bereits die Formel für das Magnetfeld eines geraden, stromdurchflossenen Leiters. Die magnetische Flussdichte \(B_1\) des Magnetfeldes des ersten Leiters beträgt in der Entfernung \(d\)
\[ B_1=\frac{\mu_0}{2\cdot\pi}\cdot \frac{I_1}{d} \]
Setzen wir diese magnetische Flussdichte in die Formel für die Lorentzkraft ein, erhalten wir:
\[ F_{2} = I_2\cdot \ell\cdot\left(\frac{\mu_0}{2\cdot\pi} \cdot \frac{I_1}{d}\right) = \frac{\mu_0}{2\cdot\pi}\cdot \frac{I_1\cdot I_2}{d}\cdot\ell \]
Dieselbe Formel ergibt sich, wenn wir die Kraft von Leiter zwei auf den Leiter eins berechnen. Daher können wir den Index bei der Kraft weglassen. Die Beziehung
| \[\begin{equation} \frac{F}{\ell} = \frac{\mu_0}{2\cdot\pi}\cdot\frac{I_1\cdot I_2}{d} \tag{13.15} \end{equation}\] |
wird Ampèresches Kraftgesetz (engl. Ampère’s force law) genannt. In dieser Formel bedeuten:
- \(F\) Kraft zwischen den beiden Leitern (in \(\mathrm{N}\))
- \(\ell\) die Länge der beiden Leiter (in \(\mathrm{m}\))
- \(I_1\) und \(I_2\), die elektrischen Stromstärken der Leiter (in \(\mathrm{C/s}\))
- \(d\) der Abstand beider Leiter (in \(\mathrm{m}\))
- \(\mu_0\), die magnetische Feldkonstante (\(1.26\cdot 10^{-6}\;\mathrm{N/A^2}\))
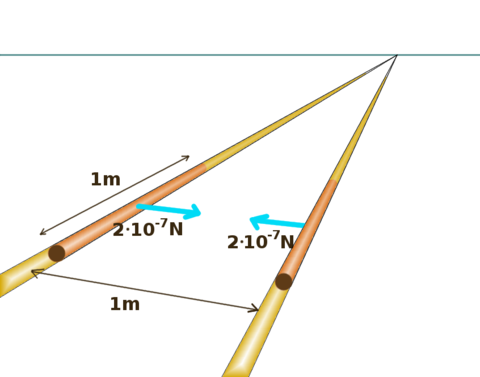
Das Ampèresches Kraftgesetz wurde bis 2019 dazu verwendet, die Basis-Einheit Ampere des Internationalen Einheitensystems festzulegen (Bild 13.64).
Befinden sich zwei parallele Leiter im Abstand von einem Meter und ist die Kraft pro einem Meter Leiter \(2\cdot10^{-7}\;\mathrm{N}\), beträgt die elektrische Stromstärke in beiden Leitern exakt \(1\;\mathrm{A}\).