13.11 Elektromotor
Jeder Blu-ray-Player, jeder Haartrockner, jede Waschmaschine, jede Küchenmaschine, jeder Roboter und jedes E-Bike (Bild 13.133) hat einen.
Die Rede ist vom Elektromotor. Er wandelt elektrische Energie in mechanische Energie um und dient so als Antrieb für eine Vielzahl von Geräten. In diesem Kapitel erfährst du über das Drehmoment von Leiterschleifen in einem Magnetfeld und über ihre Anwendungen.
13.11.1 Ausrichtung im Magnetfeld
Legst du einen drehbar gelagerten Stabmagneten in ein äußeres Feld, dreht er sich in Feldlinienrichtung. In Bild 13.134 siehst du, wie sich die Feldlinien des Gesamtfeldes (Überlagerung aus äußerem Feld und Feld des Stabmagneten) dabei „entspannen“.
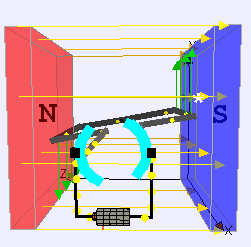
Ebenso verhält sich eine stromdurchflossene Leiterschleife (Bild 13.135). Die Pfeile zeigen die Richtung der Lorentzkraft, die auf die Leiterelektronen an diesen Stellen wirkt und die Drehung verursacht.
In beiden Fällen stoppt die Bewegung nach der Ausrichtung im Feld. Für eine anhaltende Drehung braucht es mehr.
13.11.2 Drehmoment auf eine Leiterschleife
Auf eine stromführende Leiterschleife in einem Magnetfeld wirkt die Lorentzkraft (Bild 13.135). Je nach Lage der Leiterschleife bewirken die entgegengesetzten Kräfte auf beiden Seiten der Leiterschleife eine unterschiedlich große Drehkraft (Drehmoment). Mit zunehmender senkrechter Lage wird das Drehmoment kleiner. Sobald die Leiterschleife senkrecht steht, ist das Drehmoment null. Die Größe des Drehmoments einer Spule oder Leiterschleife (Spule mit nur einer Windung) lässt sich mit folgender Formel berechnen:
| \[\begin{equation} M = N\cdot I\cdot A \cdot B\cdot\cos(\beta) \tag{13.31} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(M\), das Drehmoment auf die Spule (in \(\mathrm{Nm}\))
- \(N\), die Anzahl der Windungen der Spule (dimensionslose Zahl)
- \(I\), die Stromstärke (in \(\mathrm{A}\))
- \(A\), die Querschnittsfläche der Spule (in \(\mathrm{m^2}\))
- \(B\), die magnetische Flussdichte des äußeren Feldes (in \(\mathrm{T}\))
- \(\beta\), der Winkel zwischen der Nord-Richtung der Spule und der Feldlinienrichtung des äußeren Feldes
13.11.3 Herleitung: Drehmoment auf eine Leiterschleife
Um die Größe des Drehmoments herzuleiten, gehen wir von einer rechteckigen Leiterschleife mit einer Länge \(a\) und einer Breite \(b\) aus. Sie befindet sich, wie in Bild 13.136 gezeigt, in einem homogenen Magnetfeld. Schicken wir einen Strom \(I\) durch sie hindurch, kommt es zu einer Lorentzkraft. Entlang der Seiten \(b\) zeigt die Stromrichtung entlang der magnetischen Feldlinienrichtung, und die Lorentzkraft ist null (\(F_L = 0\)). Entlang der Seiten \(a\) stehen die Strom- und die Magnetfeldrichtung im rechten Winkel zueinander – die Lorentzkraft ist hier maximal, also \(F_L = I\cdot a\cdot B\). Da die Stromrichtungen entlang der beiden \(a\)-Seiten entgegengesetzt verlaufen, zeigen auch die Lorentzkräfte in entgegengesetzte Richtungen. Die Lorentzkraft kippt also die Leiterschleife um die eingezeichnete Symmetrie-Achse.
In der ursprünglichen Lage stehen die Kraft \(F_L\) und der Abstand \(r\) zur Drehachse im rechten Winkel zueinander. Für das Drehmoment auf einer Seite gilt daher die Formel:
\[ \begin{aligned} M = {} & r\cdot F_L \\ M = {} & \left(\frac{b}{2}\right)\cdot (I\cdot a\cdot B) \\ M = {} & \frac{1}{2}\cdot I\cdot a\cdot b\cdot B \qquad\Bigr\rvert\; A = a\cdot b\\ M = {} & \frac{1}{2}\cdot I\cdot A \cdot B \\ \end{aligned} \]
Mit \(A=a\cdot b\) dem Flächeninhalt der Leiterschleife. Beachte, dass wir bisher nur eine Seite berücksichtigt haben. Auf der anderen Seite zeigt das Drehmoment in dieselbe Richtung, und sie verstärken einander. Das Gesamtdrehmoment hat daher den doppelten Wert.
\[ M_{ges} = 2\cdot\frac{1}{2}\cdot I\cdot A \cdot B = I\cdot A \cdot B \]
Dreht sich die Leiterschleife, bleibt die Lorentzkraft auf den Seiten \(a\) unverändert (Bild 13.136), aber das Drehmoment nimmt mit dem Cosinus des Drehwinkels ab.
\[ M_{ges} = I\cdot A \cdot B\cdot\cos(\beta) \]
Steht die Leiterschleife senkrecht, ist das Drehmoment null und es kommt zu keiner weiteren Drehung.
Eine Leiterschleife entspricht einer Spule mit einer einzigen Windung (Windungszahl \(1\)). Wird statt einer einzelnen Leiterschleife eine Spule mit \(N\) Windungen verwendet, erhöht sich das Drehmoment um diesen Faktor.
\[ M_{ges} = N\cdot I\cdot A \cdot B\cdot\cos(\beta) \]
13.11.4 Drehspulinstrument
Im Gegensatz zu einem digitalen Multimeter misst ein Drehspulinstrument elektrische Größen wie Spannung, Stromstärke und Widerstand elektromechanisch. In Bild 13.137 siehst du den Aufbau eines Galvanometers (Drehspulinstrument zur Strommessung).

Bild 13.137: Aufbau eines Galvanometers nach Weston
Fließt der zu messende Strom über die Spiralfedern durch die Spule in der Mitte des Geräts, erfährt sie ein Drehmoment im Feld des Dauermagnets. Die Spiralfedern auf beiden Seiten der Spule sorgen für eine rücktreibende Kraft. Damit ist der Zeigerausschlag direkt proportional zur Stromstärke durch die Spule.
13.11.5 Einfacher Gleichstrommotor
Ein Gleichstrommotor wandelt Gleichstrom (elektrische Energie) in mechanische Energie um. Der einfachste Gleichstrommotor besteht aus einem Dauermagnet (Stator), zwischen dessen Polen sich eine drehbar gelagerte Spule (Rotor oder Anker) befindet (Bild 13.138).
Fließt Gleichstrom über die Schleifkontakte (Bürsten) durch die Ankerspule, wird sie zu einem Elektromagneten, dessen Pole sich von den Polen des Dauermagnets (Polschuhe) abstoßen oder anziehen. Es entsteht ein Drehmoment, und der Anker beginnt sich zu drehen. Um die Drehrichtung zu bestimmen, verwendest du am einfachsten die Rechte-Faust-Regel für eine Spule und überlegst dir die Abstoßung/Anziehung dieses Magneten zwischen den Magnetpolen des Stators.
Der Anker dreht sich im besten Fall allerdings nur um eine halbe Drehung und bleibt dann stehen (wenn sich die ungleichnamigen Pole von Ankerspule und Stator gegenüberstehen). Damit es zu einer dauerhaften Drehbewegung kommt, muss jede halbe Umdrehung die Ankerspule umgepolt werden. Das lässt sich elegant mit einem unterbrochenen leitenden Ring (Kommutator oder Polwender) bewerkstelligen (Bild 13.139). Während des Umpolens fließt kein Strom durch die Ankerspule. Diesen Teil der Kreisbewegung muss der Motor durch Trägheit überbrücken.
Die Geschwindigkeit eines Gleichstrommotors lässt sich über die Stromstärke der Ankerspule regeln. Zum Beispiel befindet sich bei einer klassischen Autorennbahn im Hand-Controller ein regelbarer Widerstand, der mit dem Motor in Serie geschaltet ist (Bild 13.140). Wird der Abzug gedrückt, wird der elektrische Widerstand kleiner. Damit steigt die Stromstärke, der Motor dreht schneller und das Fahrzeug beschleunigt.
Links:
- WebApp: Gleichstrom-Elektromotor
13.11.6 Verbesserter Gleichstrommotor
In Bild 13.139 kannst du außerdem erkennen, dass die Beschleunigung des Motors ruckartig erfolgt, weil das Drehmoment sich ständig ändert. Deswegen werden Anker in der Praxis mit sehr vielen Windungen gebaut (Trommelanker, Bild 13.141), damit das Drehmoment möglichst gleich groß bleibt.
Der Kupferlackdraht wird dabei um gegeneinander elektrisch isolierte und geschichtet aufgebaute Elektrobleche gewickelt. Sie sorgen einerseits dafür, dass möglichst viele Feldlinien des Stator-Magnetfeldes im Anker verlaufen und andererseits dafür, dass Verluste durch Induktionsströme möglichst klein sind. Die Bleche bestehen zusätzlich aus Weicheisen, um Verluste durch Ummagnetisierung zu verringern.
In Bild 13.142 siehst du beispielsweise das Windungsschema eines Trommelankers mit 6-teiligem Kommutatorring. Folgst du den Pfeilen vom Plus-Pol ausgehend, wirst du erkennen, dass Strom durch alle Teilwindungen des Ankers fließt. Obwohl sich der Rotor dreht, von ihm erzeugte Nord- und Süd-Pol relativ zum Stator immer nahezu an derselben Stelle. Das garantiert zu jeder Zeit ein maximales Drehmoment.
Mit dem Trommelanker wird noch ein weiteres Problem des einfachen Elektromotors behoben: Sollte der Anker unglücklicherweise nach dem Abschalten in der Stellung stehen bleiben, in der beide Kontakte des Kommutatorringes unterbrochen sind, läuft er beim Einschalten nicht wieder an und muss per Hand angeworfen werden. Bei einem Trommelanker kann die Unterbrechung des Ringes kleiner als die Breite der Bürste ausfallen, sodass in jeder Stellung Teile des Ankers mit Strom durchflossen werden. So wird garantiert, dass der Motor in jeder Stellung von allein anlaufen kann.
13.11.7 Belasteter Elektromotor
Betrachten wir zunächst einen Gleichstrommotor im Leerlauf. So wird ein Motor bezeichnet, der nichts antreiben muss (unbelasteter Motor). Da sich bei einem Elektromotor die Ankerspule durch ein Magnetfeld dreht, sind alle Voraussetzungen für elektromagnetische Induktion gegeben. Die in der Ankerspule induzierte Spannung ist nach der Lenzschen Regel ihrer Ursache entgegengerichtet. Das ist in unserem Fall die Spannung der Batterie, die den Motor antreibt. Im Idealfall – ohne Verluste – würde der Motor so lange schneller werden, bis induzierte Spannung und Batteriespannung einander gerade aufheben. Der Strom in den Ankerwindungen ist dann null! Durch Reibung ist aber immer eine geringe Last vorhanden, sodass auch im Leerlauf immer ein kleiner Strom fließt.
Jetzt belasten wir diesen Motor, indem wir ihn zum Beispiel an einer Seilwinde Arbeit verrichten lassen (Bild 13.143).
In diesem Fall verringert sich die Drehgeschwindigkeit aufgrund der Belastung, die induzierte Spannung nimmt ab und der Stromfluss im Anker steigt. Damit steigt auch die der Spannungsquelle entnommene elektrische Leistung \(U\cdot I\).
| Elektromotoren passen ihre elektrische Leistungsaufnahme automatisch an die mechanische Belastung an. |
Dieses Verhalten wird als „elastisch“ bezeichnet. Elektromotoren benötigen daher kein Getriebe, wie etwa ein Verbrennungsmotor.
13.11.8 Synchron-Motor
Beim Synchron-Motor (engl. synchronous motor) wird in den Stator-Spulen ein rotierendes äußeres Magnetfeld (Drehfeld) erzeugt. Der Rotor (in unserem Beispiel ein Stabmagnet) folgt dem äußeren Feld. Rotor und äußeres Feld drehen sich synchron mit derselben Geschwindigkeit relativ zum Stator. Ein drehendes Magnetfeld kann zum Beispiel mithilfe der zeitversetzten Ströme des Drehstroms und drei kreisförmig angeordneten, jeweils um \(120^\circ\) versetzten Spulen realisiert werden (Bild 13.144) oder mit einphasigem Wechselstrom und einem Kondensator (Kondensatormotor).
Ist das Trägheitsmoment des Rotors zu groß, überholt das rotierende Drehmagnetfeld den Rotor ständig, noch bevor er sich in Bewegung setzen kann. In diesem Fall muss der Motor angeworfen werden.
13.11.9 Bürstenloser Gleichstrommotor
Der bürstenlose Gleichstrommotor (engl. brushless motor) übernimmt die Idee des Synchron-Motors eines rotierenden Magnetfeldes, dem ein Permanentmagnet folgt. Er verwendet aber eine Steuerelektronik, um gepulste Gleichströme durch die unterschiedlichen Spulen zu schicken und so das gewünschte rotierende Magnetfeld zu erzeugen.
In Bild 13.145 siehst du den bürstenlosen Motor eines PC-Lüfters. Links siehst du den Stator mit zwei Spulen und rechts den Rotor mit sechs grauen Permanentmagneten.
Der Vorteil gegenüber einem Gleichstrommotor mit Bürsten besteht einerseits darin, dass die Geschwindigkeit und das Drehmoment sehr genau gesteuert werden können. Andererseits gibt es keinen direkten Kontakt zwischen Rotor und Stator und damit keinen Verschleiß durch Bürstenabnützung.
13.11.10 Induktionsmotor
Ein Induktionsmotor (engl. induction motor) verwendet wie der Drehstrom Synchron-Motor ebenfalls ein äußeres Drehfeld. Statt eines Permanentmagnets wird als Rotor aber ein käfigförmiger Kurzschlussläufer verwendet (Bild 13.146). Durch das magnetische Drehfeld der Stator-Spulen wird in dem Metallkäfig ein Strom induziert. Diese Induktionsströme machen den Käfig zu einem Elektromagneten, der dem äußeren Feld hinterherläuft.
Würden sich Käfig und äußeres Magnetfeld mit derselben Geschwindigkeit drehen, gäbe es keine magnetische Flussänderung durch den Käfig und damit weder einen induzierten Strom noch ein induziertes Magnetfeld. Um eine minimale Flussänderung zu erhalten, muss der Käfig immer ein wenig langsamer als das Drehfeld rotieren. Daher wird der Induktionsmotor auch als Asynchron-Motor bezeichnet. Die Differenz der beiden Rotationsgeschwindigkeiten wird Schlupf (engl. slip) genannt.
Je stärker der Käfig in seiner Bewegung behindert wird, desto größer ist das induzierte Magnetfeld und desto größer das Drehmoment – ein Asynchron-Motor passt sich also seiner Belastung an.
Das Prinzip des Induktionsmotors wird auch in Elektroautos verwendet. Ein großer Vorteil besteht darin, dass beim Abbremsen und Bergabfahren der Käfig als elektrischer Generator verwendet wird und ein Teil der Bewegungsenergie wieder in elektrische Energie umgewandelt und im Akkumulator gespeichert werden kann (Rekuperation).
13.11.11 Homopolarmotor
Der Homopolarmotor (engl. homopolar motor) ist der einfachste Gleichstrommotor. Im Gegensatz zum gewöhnlichen Elektromotor besitzt er keinen Kommutator, der die Stromrichtung wechselt. Du kannst ihn sehr einfach aus
- einer Batterie,
- einem Knopfmagneten
- einem Stück Draht
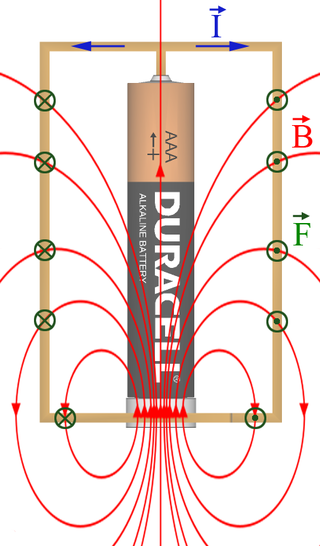
selber bauen (Bild 13.147).
Die Anordnung ist so gewählt, dass die Magnetfeldrichtung \(B\) und die Stromrichtung \(I\) an einer Stelle zu allen Zeiten denselben Winkel einschließen. Die Lorentzkraft ist somit immer gleich groß und erzeugt ein konstantes Drehmoment entlang der Drehachse (Bild 13.148).
Homopolarmotoren erreichen nur ein kleines Drehmoment und werden daher in der Praxis kaum verwendet.
Links:
- Video: Einfacher Homopolarmotor