13.10 Elektrischer Generator
Ein Fahrrad wird meistens zur Fortbewegung benutzt. Du kannst mit seiner Hilfe aber auch deine Muskelkraft für den Betrieb eines Radios oder zum Laden deines Smartphone-Akkus verwenden (Bild 13.116).
Eine Maschine, die aus mechanischer Bewegung eine elektrische Spannung erzeugt, wird allgemein elektrischer Generator (engl. electric generator) genannt – du kannst ihn im Bild 13.116 als Walze am Hinterrad erkennen. Der elektrische Generator ist die Grundlage unserer elektrifizierten Welt. In jedem Kraftwerk befinden sich einer oder mehrere davon.
In diesem Kapitel erfährst du unter anderem, wie ein elektrischer Generator funktioniert und wie Wechselstrom in Gleichstrom umgewandelt werden kann.
13.10.1 Wechselstromgenerator
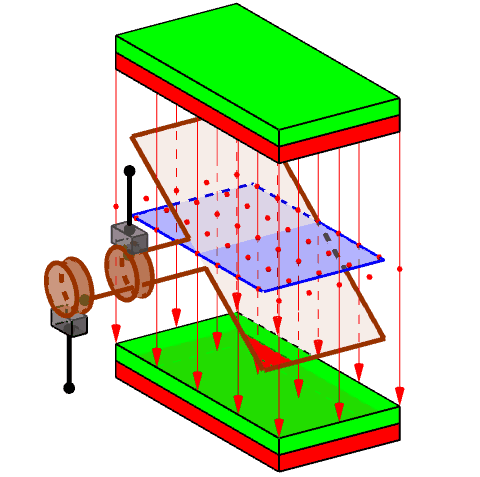
In Bild 13.117 siehst du den Aufbau eines einfachen Wechselstromgenerators (engl. alternating current generator oder alternator).
Im Magnetfeld (Erregerfeld) eines Permanentmagneten (Stator) dreht sich eine Leiterschleife (Rotor). Durch die periodische magnetische Flussänderung durch die Leiterschleife wird Spannung induziert (Faradaysches Induktionsgesetz). Diese Spannung kann mithilfe von Schleifkontakten (Metall- oder Kohlebürsten) an zwei Schleifringen abgegriffen werden. Du erhältst dabei eine sinusförmige Wechselspannung (Bild 13.118).
Diese Bauform wird als Außenpolgenerator bezeichnet. Da es nur auf die Flussänderung ankommt, erhältst du dasselbe Resultat, wenn sich ein Permanentmagnet in einer Leiterschleife dreht – also Stator und Rotor die Plätze tauschen. Diese Bauform eines Generators wird Innenpolgenerator genannt.
Links:
- Simulation: Wechselstromgenerator
13.10.2 Induktionsspannung einer rotierenden Leiterschleife
In diesem Abschnitt möchten wir uns ansehen, wie es zu einer sinusförmigen Wechselspannung kommt. In Bild 13.119 siehst du eine einzelne Leiterschleife der Querschnittsfläche \(A\) in einem homogenen Magnetfeld \(B\). Die Stellung der Leiterschleife wird durch den Drehwinkel \(\varphi\) angegeben.
Für den momentanen magnetischen Fluss \(\Phi\) durch die Leiterschleife gilt:
\[ \Phi = B\cdot A\cdot\cos(\varphi) \]
Dreht sich die Leiterschleife mit einer konstanten Winkelgeschwindigkeit \(\omega\), gilt für den Drehwinkel \(\varphi=\omega\cdot t\) und der magnetische Fluss zu einem Zeitpunkt \(t\) ist:
\[ \Phi = B\cdot A\cdot\cos(\omega\cdot t) \]
Für die in der Schleife induzierte Spannung \(u_{\textrm{ind}}\) ist nicht der magnetische Fluss selbst, sondern die zeitliche magnetische Flussänderung entscheidend.
\[ U(t) = -\frac{d\Phi}{dt} = -\frac{d}{dt} (B\cdot A\cdot\cos(\omega\cdot t)) \]
Die zeitliche Ableitung liefert die Formel für die induzierte Spannung
\[ U(t) = B\cdot A\cdot\omega\cdot\sin(\omega\cdot t) \]
In dieser Formel bedeuten:
- \(U\), die induzierte Spannung (in \(\mathrm{V}\))
- \(B\), die magnetische Flussdichte (in \(\mathrm{T}\))
- \(A\), die Querschnittsfläche der Leiterschleife (in \(\mathrm{m}^2\))
- \(\omega\), die Winkelgeschwindigkeit (in \(\mathrm{rad}/\mathrm{s}\))
- \(t\), die Zeit (in \(\mathrm{s}\))
Da der Sinuswert maximal 1 sein kann, ist die größte Spannung \(U_{\textrm{max}}=B\cdot A\cdot\omega\) (Maximal- oder Scheitelspannung) und wir erhalten:
| \[\begin{equation} U(t) = U_{\textrm{max}}\cdot\sin(\omega\cdot t) \tag{13.30} \end{equation}\] |
Eine gleichförmig rotierende Leiterschleife in einem homogenen Magnetfeld erzeugt also eine sinusförmige Wechselspannung (Das Vorzeichen der Spannung ändert sich periodisch).
Links:
- WebApp: Der Wechselstromgenerator
13.10.3 Anschauliche Herleitung der Generatorspannung
In Bild 13.120 siehst du eine gleichförmig rotierende Leiterschleife zu unterschiedlichen Zeitpunkten und ihre Stellung in einem homogenen Magnetfeld. Die Kurve darunter zeigt den zeitlichen Verlauf des magnetischen Flusses \(\Phi_\text{B}\) durch diese Leiterschleife.
Wie bei jeder Funktion kannst du die momentane Änderungsrate als Tangentensteigung der Kurve an dieser Stelle erkennen. Betrachten wir einen Zeitpunkt, zu dem der magnetische Fluss maximal oder minimal ist (zum Beispiel Punkt 1) verläuft die Tangente an die Kurve waagrecht. Zu diesen Zeitpunkten ist die Tangentensteigung null und es kommt zu keiner zeitlichen Flussänderung und damit auch zu keiner induzierten Spannung. Zu Zeitpunkten, an denen der magnetische Fluss durch die Schleife null ist (zum Beispiel Punkt 2), hat die Tangentensteigung ihre größte Wert. In diesem Bereich findet die maximale Flussänderung statt – die induzierte Spannung ist hier am größten. Folgt der zeitliche Verlauf des magnetischen Flusses einer Kosinus-Kurve, ergibt sich daraus für die induzierte Spannung \(U(t)\) eine Sinus-Funktion. Dass bei einer positiven Steigung der Fluss-Kurve das Vorzeichen der Spannung negativ ist, folgt aus der Lenzschen Regel.
13.10.4 Wechselstromgenerator unter Last
Verbindest du einen handbetriebenen Wechselstromgenerator mit einem Verbraucher (zum Beispiel einer Lampe), wirst du einen großen Unterschied zum unbelasteten Generator feststellen. Das Drehen der Kurbel ist jetzt viel mühsamer, und du spürst einen deutlichen Widerstand gegen die Bewegung.
Der Betrieb der Lampe erfordert elektrische Arbeit, die du beim Drehen des Rotors durch das Erregerfeld mechanisch verrichten musst. Ist ein Verbraucher angeschlossen, fließt Strom durch die Leiterschleife. Durch den Stromfluss kommt es zu einer Lorentzkraft, die nach der Lenzsche Regel ihrer Ursache – in diesem Fall deiner Drehbewegung – entgegenwirkt (Bild 13.121).
13.10.5 Dynamoelektrisches Prinzip
Starke Permanentmagnete sind teuer und außerdem können sie nur bis zu einer bestimmten maximalen Stärke hergestellt werden. Daher ist die Idee naheliegend, bei großen Generatoren für das Erregerfeld statt eines Permanentmagnets einen Elektromagneten zu verwenden und ihn parallel (Nebenschlussmaschine) oder in Serie (Reihenschlussmaschine) zu der Rotorwicklung zu schalten (Bild 13.122). Auf diese Weise liefert der Generator selbst den für das Erregerfeld notwendigen Strom.
Dabei gibt es ein offensichtliches Problem. Zu Beginn fließt kein Strom und der Elektromagnet erzeugt kein Erregerfeld. Wird der Rotor gedreht, kommt es zu keiner Flussänderung und somit wird auch keine Spannung induziert.
In der Praxis stellt sich jedoch heraus, dass der Eisenkern der Erregerspule ein geringes Restmagnetfeld (Remanenz) aus dem letzten Betrieb behält. Dieses geringe Magnetfeld genügt, um beim Drehen der Induktionsspule auch schon zu Beginn einen geringen Strom zu induzieren. Durch positive Rückkopplung erhöht dieser Strom das Erregerfeld. Dadurch wird wieder mehr Strom in der Spule induziert und so weiter, bis das Erregerfeld maximal ist (magnetische Sättigung). Dieses Verhalten der Selbsterregung (engl. self-excitation) wird dynamoelektrisches Prinzip (engl. dynamoelectric principle) genannt und kommt bei allen großen Generatoren in Kraftwerken zur Anwendung.
Vor der Auslieferung werden die Eisenkerne daher einmal magnetisiert. Sollte – zum Beispiel bei zu langem Stillstand – zu wenig Restmagnetismus vorhanden sein, muss der Eisenkern vor dem Betrieb mit einer externen Energiequelle (gering) magnetisiert werden.
13.10.6 Drehstromgenerator
In Bild 13.123 siehst du den Aufbau eines Drehstromgenerators. Hier sind drei gleiche, voneinander unabhängige Induktionsspulen jeweils um \(120^\circ\) (\(=360^\circ/3\)) versetzt um den Rotor angeordnet. Auf diese Weise werden drei unabhängige, gleich große Wechselspannungen erzeugt, die jeweils um eine drittel Periode versetzt sind.
Diese drei Ströme werden zusammen als Drei-Phasen-Wechselstrom oder Drehstrom bezeichnet. Er kann nicht nur zum Betrieb von Drehstrommotoren verwendet werden, sondern hat auch für die Übertragung von elektrischer Energie einen großen Vorteil. Jedes Kraftwerk erzeugt daher Drei-Phasen-Wechselstrom.
13.10.7 Einweggleichrichter
Eine Steckdose liefert immer Wechselspannung. Einige Verbraucher wie ein Computer benötigen zum Betrieb aber Gleichspannung. Das Umwandeln eines Wechselstroms in Gleichstrom wird Gleichrichten (engl. rectification) genannt.
Die einfachste Methode, einen Strom gleichzurichten, ist der Einbau einer Diode in den Wechselstromkreis (Bild 13.124).
Da eine Diode Strom nur in eine Richtung passieren lässt, sperrt sie jede zweite Halbwelle des angelegtenWechselstroms. Du erhältst den Stromverlauf in Bild 13.125.
Durch das Unterdrücken der Hälfte aller Halbwellen kann im Vergleich zu einem Stromkreis ohne Diode nur die halbe Leistung entnommen werden.
13.10.8 Brückengleichrichter
Im Gegensatz zum Einweggleichrichter wird bei der Vollweggleichrichtung (engl. full wave rectifier) jede Halbwelle durchgelassen, lediglich das Vorzeichen wird vertauscht.
Eine Möglichkeit, das zu erreichen, ist die Graetzsche Brückenschaltung (benannt nach Leo Graetz). In Bild 13.126 siehst du diese Schaltung aus vier Dioden. Um den Verlauf des Stromes durch die Schaltung besser nachvollziehen zu können, findest du in Bild 13.127 eine umgezeichnete Variante der Brückenschaltung, bei der die Stromwege für die positive und die negative Halbwelle getrennt gezeichnet sind.
Durch diese Schaltung erhältst du einen pulsierenden Gleichstrom (engl. pulsating direct current, Bild 13.128)
13.10.9 Glättung von pulsierendem Gleichstrom
Obwohl pulsierender Gleichstrom nur eine Stromrichtung aufweist, ist er aber noch weit von dem konstanten Gleichstrom einer Gleichspannungsquelle – etwa der einer Batterie – entfernt. Die meisten elektronischen Bauteile funktionieren nur dann, wenn die angelegte Spannung (fast) gleich groß bleibt.
In diesem Fall muss der pulsierende Gleichstrom noch geglättet (engl. smoothing) werden. In der Praxis wird dazu üblicherweise ein Kondensator verwendet, der dem Verbraucher parallel geschaltet ist (13.129).
Er verringert die Spannungsschwankungen, indem er elektrische Energie während der Spannungsspitzen zwischenspeichert und sie dann beim Abfallen der Generator-Spannung abgibt. Den zeitlichen Verlauf eines auf diese Weise geglätteten pulsierenden Gleichstromes siehst du in Bild 13.130 – er kommt einem echten Gleichstrom schon sehr nahe.
13.10.10 Windkessel-Effekt
Eine mechanische Version der Glättung eines pulsierenden Gleichstroms findest du bei deinem Herzen. Während eines Herz-Zyklus erzeugt dein Herz durch ruckartiges Zusammenziehen des Herzmuskels kurzfristig einen sehr hohen Druck (Systole) und entspannt sich dann kurzzeitig (Diastole). Den zeitlichen Druckverlauf in der linken Herzkammer siehst du in Bild 13.131 als blaue Kurve.

Bild 13.131: Druck in der Aorta (rote Kurve) und in der linken Herzkammer (blaue Kurve) über zwei Herz-Zyklen
Die Wände der großen Arterien nahe dem Herzen sind sehr elastisch. Diese Arterien dehnen sich aus, wenn der Blutdruck während der Systole ansteigt, und ziehen sich wieder zusammen, wenn der Blutdruck während der Diastole sinkt (Bild 13.132, unten). Die Dehnarbeit wird also als Spannenergie zwischenzeitlich im Gewebe gespeichert, um die Ruhephase im Herz-Zyklus zu überbrücken (Bild 13.131, rote Kurve). Das gleicht dem Verhalten des Kondensators, der elektrische Energie kurzfristig speichert. Durch das Puffern des Drucks wird ein viel konstanterer Blutstrom durch den Körper erzeugt.
Dieser Effekt wird Windkessel-Effekt (engl. windkessel effect) genannt. Bei Wasserpumpen, die stoßartig arbeiten, wird ein luftgefüllter Behälter verwendet, der für einen möglichst gleichmäßigen Wasserstrom sorgt (Bild 13.132, oben). Die Luft im Behälter („Windkessel“) lässt sich leicht zusammendrücken und kann so Druckenergie speichern.