13.9 Induktion im eigenen Stromkreis
Vorsicht vor dem Kaugummi in Bild 13.108. Wenn du an dem Streifen ziehst, erhältst du einen kleinen Elektroschock!
Obwohl die Batterien in diesen Geräten nur eine Spannung von ein paar wenigen Volt besitzen, können professionelle Taser wiederholte Elektroschocks von mehreren Tausend Volt erzeugen!
In diesem Kapitel geht es um die Selbstinduktion, die gespeicherte Energie in einer Spule und die Parallel- und Serienschaltung von Spulen. Außerdem erfährst du das Prinzip hinter dem Elektroschocker…
13.9.1 Einführungsexperiment zur Selbstinduktion
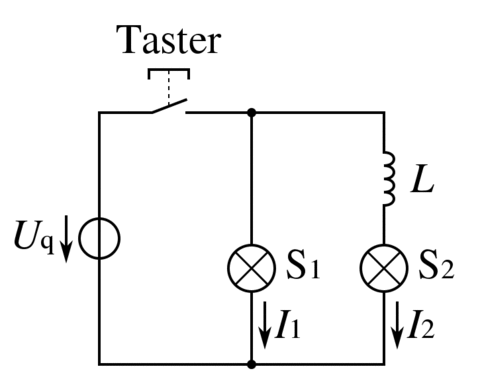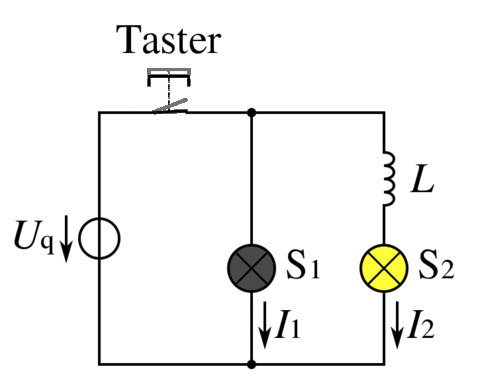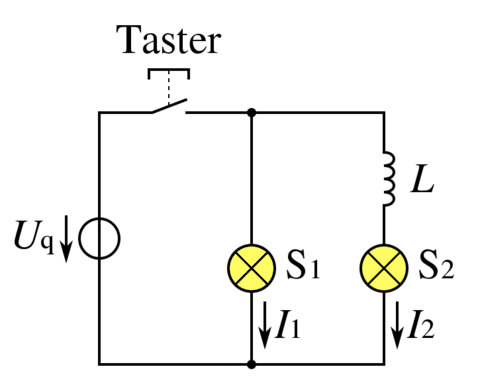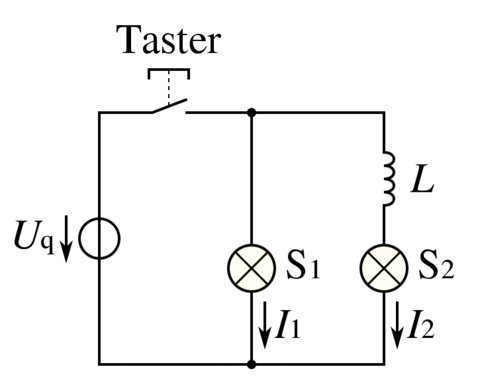
In Bild 13.109 siehst du eine Parallelschaltung von zwei Lämpchen. Allerdings befindet sich im zweiten Stromzweig zusätzlich eine Spule in Serie mit dem Lämpchen. Schaltest du ein, leuchtet das Lämpchen im Zweig ohne Spule sofort auf, während das Lämpchen im Zweig mit der Spule erst allmählich seine volle Helligkeit erreicht. Beim Ausschalten gehen beide Lämpchen nur allmählich aus.
Aus dem Verhalten der Lämpchen können wir zwei Dinge schließen:
- Beim Einschalten behindert die Spule den Stromfluss.
- Nach dem Ausschalten liefert die Spule Energie für einen kurzfristigen weiteren Stromfluss.
Mit diesen beiden Effekten und den damit verbundenen Begriffen werden wir in diesem Kapitel beschäftigen.
13.9.2 Selbstinduktion
Ändert sich das Magnetfeld in einer Spule, kommt es zu einer Induktionsspannung. Das gilt aber nicht nur für eine zweite Spule in der Nähe, sondern auch für die felderregende Spule (Feldspule) selbst. Diese in der Feldspule auftretende Induktion wird Selbstinduktion (engl. self induction) genannt. Nach der Lenzschen Regel ist die Selbstinduktionsspannung immer so gerichtet, dass sie ihrer Ursache – in unserem Fall der Stromänderung im Stromkreis – entgegenwirkt.
Wir nehmen den Stromkreis aus Bild 13.109 und ersetzen die Lämpchen durch zwei Widerstände. Der Widerstand im Zweig ohne Spule ist außerdem regelbar (13.110).
In Bild 13.111 siehst du den Verlauf von Spannung und Stromstärke in diesem Stromkreis. Durch die in der Spule induzierte Gegenspannung, steigt die Stromstärke nach dem Einschalten nur allmählich an und erreicht schließlich ihren maximalen Wert, der durch den ohmschen Widerstand der Schaltung begrenzt ist.
Im Gegensatz dazu bricht die Batteriespannung beim Ausschalten schlagartig weg und der Strom kommt schnell zum Erliegen. Bei kleinen Widerständen (Last) ist das Verhalten beim Ein- und Ausschaltvorgang noch annähernd symmetrisch (13.111 a). Je größer allerdings die Last, desto schneller kommt der Strom nach dem Abschalten zum Erliegen und desto größer ist die Flussänderung durch die Spule und die damit verbundene Spannungsspitze durch die Selbstinduktion (13.111 b).
Das Entstehen von großen Spannungsspitzen beim Öffnen des Schaltkreises ist das Funktionsprinzip des Funkeninduktors (engl. spark coil), der Zündspule beim Otto-Motor oder auch des Elektroschockers aus dem Kapitelanfang.
13.9.3 Herleitung Selbstinduktion
Das Induktionsgesetz lautet:
\[ U_\mathrm{ind} = - \frac{\Delta\Phi_B}{\Delta t} \]
Da es in jeder einzelnen Wicklung der Spule zu selben Induktionsspannung kommt, gilt für eine Spule mit \(N\) Windungen:
\[ U_\mathrm{ind} = - N\cdot \frac{\Delta\Phi_B}{\Delta t} \]
\(\Delta \Phi_B\) bedeutet die Änderung des magnetischen Flusses, also \(\Delta(A\cdot B)\). Da die Querschnittsfläche der Spule unverändert bleibt, vereinfacht sich der Ausdruck bei der Selbstinduktion zu \(A\cdot \Delta B\) und wir erhalten:
\[ U_\mathrm{ind} = - N\cdot \frac{A\cdot \Delta B}{\Delta t} \]
Für das Magnetfeld einer stromdurchflossenen Spule gilt:
\[ B=\mu \cdot \frac{N}{\ell}\cdot I \]
Einsetzen in das Induktionsgesetz liefert:
\[ U_\mathrm{ind} = - N\cdot \frac{A}{\Delta t}\cdot \Delta \left(\mu \cdot \frac{N}{\ell}\cdot I\right) \]
Bis auf die Stromstärke \(I\) sind aber alle Größen im Klammerausdruck konstant und lassen sich aus dem Delta herausheben. Umstellen der Größen liefert:
\[ U_\mathrm{ind} = - \frac{\mu \cdot N^2 \cdot A}{\ell}\cdot \frac{\Delta I}{\Delta t} \]
Im linken Faktor kommen nur Größen vor, die von der jeweiligen Spule abhängen. Sie werden zu einer Größe \(L\) (Induktiviät) zusammengefasst. Und damit erhalten wir:
\[ U_\mathrm{ind} = - L\cdot \frac{\Delta I}{\Delta t} \]
13.9.4 Induktivität
Die Induktivität \(L\) (engl. inductance) ist eine Kenngröße jeder Spule.
Die Induktivität einer Spule ist vergleichbar mit der Kapazität eines Kondensators. Sie bestimmt zum Beispiel, wie viel Energie – genauer gesagt magnetische Feldenergie – in einer Spule gespeichert ist, wenn sie mit einer bestimmten Stromstärke durchflossen wird. Je höher die Induktivität, desto mehr Energie kann die Spule speichern und desto größer ist ihr Widerstand gegen Änderungen des Stromflusses. Daher bestimmt sie auch die Steigung der Stromkurve beim Einschaltvorgang – je größer die Induktivität, desto geringer die Steigung (Bild 13.112).
Die Einheit der Induktivität kann über die Formel der Selbstinduktionsspannung hergeleitet werden:
\[ [L]=\frac{[U]\cdot [t]}{[I]} = 1\;\frac{\text{V}\cdot \text{s}}{\text{A}}=1\;\mathrm{\Omega}\cdot \text{s} = 1\;\mathrm{H} \]
Zu Ehren von Joseph Henry trägt die Einheit „Ohm-Sekunde“ den Namen Henry.
Die Induktivität einer Spule hängt von vielen Faktoren ab, wie dem Spulenmaterial, der Anzahl und dem Durchmesser der Wicklungen, Form der Wicklungen, dem Material und der Form des Kernmaterials. Sie wird daher meist experimentell ermittelt, zum Beispiel über ihr Resonanzverhalten in einem elektrischen Schwingkreis.
13.9.5 Induktivität einer Zylinderspule
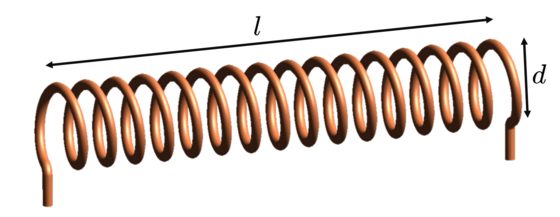
Für eine zylinderförmige Spule (Bild 13.113) kann die Induktivität durch folgende Formel berechnet werden (ohne Herleitung):
\[\begin{equation} L=\mu \cdot \frac{A\cdot N^2}{\ell} \tag{13.23} \end{equation}\]
In dieser Formel bedeuten:
- \(L\), die Induktivität der Spule (in \(\mathrm{H}\))
- \(\mu\), die magnetische Permeabilität des Kernmaterials (in \(\mathrm{N/A^2}\))
- \(N\), die Anzahl der Wicklungen (dimensionslose Zahl)
- \(A\), die Querschnittsfläche der Spule (in \(\mathrm{m^2}\))
- \(\ell\), die Länge der Zylinderspule (in \(\mathrm{m}\))
13.9.6 Selbstinduktionsspannung
Die an einer Spule auftretende Selbstinduktionsspannung hängt von der Spule (ihrer Induktivität) und von der Stärke der Änderung des Stromflusses ab.
| \[\begin{equation} U_\mathrm{ind} = - L\cdot \frac{\Delta I}{\Delta t} \tag{13.24} \end{equation}\] |
In dieser Formel bedeuten:
- \(U_\mathrm{ind}\), die in der Spule induzierte Spannung (in \(\mathrm{V}\))
- \(L\), die Induktivität der Spule (in \(\mathrm{H}\))
- \(\Delta I/\Delta t\), die zeitliche Änderung der Stromstärke in der Spule (in \(\mathrm{A}/\mathrm{s}\))
Beachte das Minus in der Formel. Es ist ein Ausdruck der Lenzschen Regel.
13.9.7 Feldenergie einer Spule
Die Formel für die in einer stromdurchflossenen Spule gespeicherte [magnetische Feldenergie][#magnetic-energy] lautet:
| \[ E_\text{mag} = \frac{L\cdot I^2}{2} \tag{13.25} \] |
In dieser Formel bedeuten:
- \(E_\text{mag}\), die in der Spule gespeicherte Feldenergie (in \(\mathrm{J}\))
- \(L\), die Induktivität der Spule (in \(\mathrm{H}\))
- \(I\), die Stromstärke des Stromes durch die Spule (in \(\mathrm{A}\))
Beachte: Die Formel für die in einem Kondensator gespeicherte elektrische Energie hat eine ganz ähnliche Struktur.
13.9.8 Herleitung: Feldenergie einer Spule
Bereits im Einführungsexperiment zur Selbstinduktion haben wir festgestellt, dass in einer stromdurchflossenen Spule Energie in Form von magnetischer Feldenergie gespeichert ist. In diesem Abschnitt möchten wir die Größe dieser gespeicherten Energie mithilfe der Infinitesimalrechnung herleiten.
Nach dem Abschalten übernimmt die Spule die Rolle der Spannungsquelle. Dabei beträgt die momentane Leistung
\[ P = {U_{\text{i}}}\left( t \right) \cdot I\left( t \right)\; \]
Beachte, dass sich sowohl Spannung als auch Stromstärke mit der Zeit ändern. Setzen wir die Definition der Selbstinduktionsspannung
\[ {U_{\text{i}}}\left( t \right)=-L \cdot \frac{{dI(t)}}{{dt}} \]
in die Leistungsformel ein, erhalten wir:
\[\begin{equation} P = -L \cdot \frac{{dI(t)}}{{dt}} \cdot I\left( t \right) \tag{13.26} \end{equation}\]
Wählen wir die folgenden Bezeichnungen
- \({E_{\text{mag,0}}}\): die gesamte gespeicherte magnetische Feldenergie der Spule vor dem Abschalten
- \({E_{\text{mag}}}(t)\): die zum Zeitpunkt \(t\) noch verbleibende magnetische Feldenergie in der Spule
- \(E(t)\): die bis zum Zeitpunkt \(t\) an die Umgebung abgegebene Energie
gilt nach dem Energieerhaltungssatz die folgende Beziehung:
\[ {E_{\text{mag}}}(t) = {E_{\text{mag,0}}} - E(t) \]
Differenzieren wir diese Gleichung, erhalten wir:
\[ \frac{{d{E_{\text{mag}}}\left( t \right)}}{{dt}} = - \frac{{dE\left( t \right)}}{{dt}} \]
Wobei die Konstante \({E_{\text{mag,0}}}\) durch die Ableitung zu null wird. Die zeitliche Ableitung der Energie (rechte Seite) entspricht aber gerade der Leistung und wir können den Ausdruck in Gleichung ((13.26)) dafür einsetzen und erhalten:
\[ \frac{{d{E_{\text{mag}}}\left( t \right)}}{{dt}} = L\cdot\frac{{dI\left( t \right)}}{{dt}} \cdot I\left( t \right) \]
Wenn wir eine Funktion finden, die abgeleitet die rechte Seite dieser Gleichung ergibt, haben wir unsere gesuchte Lösung für \(E_{\text{mag}}\). Die folgende Beziehung erfüllt diese Bedingung:
\[ {E_{\text{mag}}}(t) = \frac{1}{2} \cdot L \cdot I^2(t) \]
13.9.9 Serienschaltung von Spulen
In Bild 13.114 sind mehrere Spulen in Serie geschaltet.
Haben diese Spulen die Induktivitäten von \(L_1\), \(L_2\) bis \(L_n\) und beeinflussen sich diese Spulen nicht gegenseitig, wenn sie etwa weit voneinander entfernt oder voneinander abgeschirmt sind, dann verhalten sie sich wie eine einzige Spule mit der Induktivität:
| \[\begin{equation} L_\mathrm{ges} = L_1 + L_2 + \ldots + L_n \tag{13.27} \end{equation}\] |
Die Gesamtinduktivität \(L_\mathrm{ges}\) wird wie der Gesamtwiderstand bei einer Serienschaltung von Widerständen berechnet.
13.9.10 Herleitung: Gesamtinduktivität einer Serienschaltung
Sind die Spulen wie in Bild 13.114 in Serie angeordnet, addieren sich ihre Selbstinduktionsspannungen.
\[ \begin{aligned} U_\mathrm{ges} = {} & U_1 + U_2 + \ldots + U_\mathrm{n} \\ U_\mathrm{ges} = {} & L_1\cdot \frac{\Delta I_1}{\Delta t} + L_2\cdot \frac{\Delta I_2}{\Delta t} + \ldots + L_\mathrm{n}\cdot \frac{\Delta I_\mathrm{n}}{\Delta t} \\ \end{aligned} \]
Da sich alle Spulen aber in einem einzigen Stromzweig befinden, muss der Strom (und damit auch die zeitliche Änderung des Stromes) für alle Spulen gleich sein. Damit entfällt der Index bei den Strömen und \(\Delta I/\Delta t\) kann aus allen Summanden herausgehoben werden:
\[ \begin{aligned} U_\mathrm{ges} = {} & L_1\cdot \frac{\Delta I}{\Delta t} + L_2\cdot \frac{\Delta I}{\Delta t} + \ldots + L_\mathrm{n}\cdot \frac{\Delta I}{\Delta t} \\ = {} & (L_1 + L_2 + \ldots + L_\mathrm{n})\cdot \frac{\Delta I}{\Delta t} \\ = {} & L_\mathrm{ges} \cdot \frac{\Delta I}{\Delta t} \\ \end{aligned} \]
mit
\[ L_\mathrm{ges} = L_1 + L_2 + \ldots + L_n \]
13.9.11 Parallelschaltung von Spulen
In Bild 13.115 sind mehrere Spulen in einer Parallelschaltung angeordnet.
Haben diese Spulen die Induktivitäten von \(L_1\), \(L_2\) bis \(L_n\) und beeinflussen sich diese Spulen nicht gegenseitig, wenn sie etwa weit voneinander entfernt oder voneinander abgeschirmt sind, dann verhalten sie sich wie eine einzige Spule mit der Induktivität:
| \[\begin{equation} \frac{1}{L_\mathrm{ges}} = \frac{1}{L_1} + \frac{1}{L_2} + \ldots + \frac{1}{L_n} \tag{13.28} \end{equation}\] |
Die Gesamtinduktivität \(L_\mathrm{ges}\) wird wie der Gesamtwiderstand bei einer Parallelschaltung von Widerständen berechnet. Insbesondere gilt daher für zwei Spulen in Parallelschaltung:
\[\begin{equation} L_\mathrm{ges} = \frac{L_1\cdot L_2}{L_1 + L_2} \tag{13.29} \end{equation}\]
13.9.12 Herleitung: Gesamtinduktivität einer Parallelschaltung
Wir gehen von \(n\) Spulen mit den Induktivitäten \(L_1\), \(L_2\) bis \(L_n\) aus, die wie in Bild 13.115 in einer Parallelschaltung verbunden sind. Eine Parallelschaltung ist ein Stromteiler. Es gibt daher bis zu \(n\) unterschiedliche Ströme \(I_1\), \(I_2\),…, \(I_n\) mit dem Gesamtstrom
\[ I_\mathrm{ges} = I_1 + I_2 + \ldots + I_n \]
Die Einzelspannungen sind dabei jeweils gleich groß der Gesamtspannung:
\[ U_\mathrm{ges} = U_1 = U_2 = \ldots = U_n \]
Der Spannungsabfall kann durch die Selbstinduktionsspannung ausgedrückt werden:
\[ \begin{aligned} U_\mathrm{ges} = {} & L_\mathrm{ges} \cdot \frac{\Delta I_\mathrm{ges}}{\Delta t} &&\qquad\Bigr\rvert\cdot \frac{1}{L_\mathrm{ges}} \\ \frac{U_\mathrm{ges}}{L_\mathrm{ges}}= {} & L_\mathrm{ges} \cdot \frac{\Delta (I_1 + I_2 + \ldots + I_n)}{\Delta t} \\ = {} & \left(\frac{\Delta I_1}{\Delta t} + \frac{\Delta I_2}{\Delta t} + \ldots + \frac{\Delta I_n}{\Delta t} \right) \\ = {} & \left(\frac{U_\mathrm{ges}}{L_1} + \frac{U_\mathrm{ges}}{L_2} + \ldots + \frac{U_\mathrm{ges}}{L_n} \right) \\ = {} & U_\mathrm{ges}\cdot \left(\frac{1}{L_1} + \frac{1}{L_2} + \ldots + \frac{1}{L_n} \right) &&\qquad\Bigr\rvert\cdot \frac{1}{U_\mathrm{ges}} \\ \frac{1}{L_\mathrm{ges}}= {} & \frac{1}{L_1} + \frac{1}{L_2} + \ldots + \frac{1}{L_n} \end{aligned} \]
Und damit erhalten wir die Gleichung (13.28).