13.17.1 Idealer Schwingkreis

Ein idealer Schwingkreis ist ein Stromkreis, der nur aus einem Kondensator und einer Spule besteht. Der ohmsche Widerstand wird dabei vorläufig vernachlässigt. Wir beginnen zunächst damit, den Kondensator mithilfe einer externen Spannungsquelle zu laden und klemmen diese danach ab (Bild 13.208).

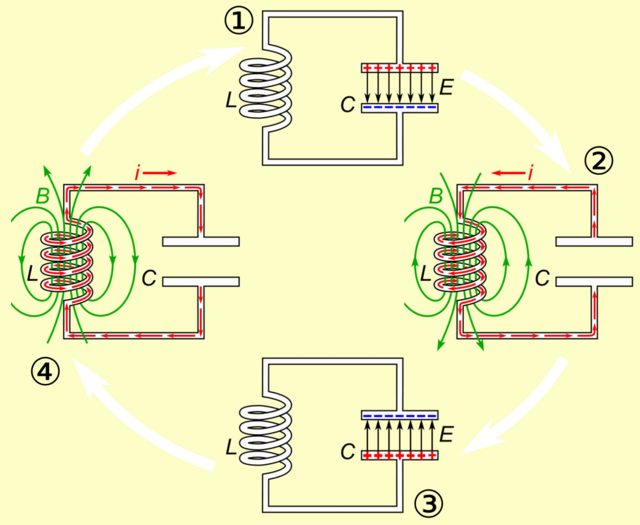
Bild 13.208: Zyklus eines idealen Schwingkreises (als Animation)

Der geladene Kondensator besitzt elektrische Feldenergie (1). Diese treibt die Ladungen beim Entladen des Kondensators an und es fließt ein elektrischer Strom durch die Spule. Nach der Lenzschen Regel behindert die Spule zunächst den Stromfluss, indem sie ein magnetisches Feld aufbaut, das diesem Strom entgegenwirkt (Selbstinduktion). Ist der Kondensator schließlich entladen, ist die Energie als magnetische Feldenergie in der Spule gespeichert (2). Der Stromfluss würde jetzt zum Erliegen kommen, aber nach der Lenzsche Regel erhält die Spule den Stromfluss weiter aufrecht. Als Energiequelle dient das Magnetfeld, das sich dabei wieder abbaut. Die Ladungen bewegen sich weiter auf die gegenüberliegende Kondensatorplatte und bilden dort ein elektrisches Feld mit umgekehrter Polung (3). Jetzt wiederholt sich der Vorgang in umgekehrter Richtung (4).

13.17.2 Thomsonsche Schwingungsgleichung

So wie jeder mechanische Oszillator besitzt auch ein Schwingkreis eine Eigenfrequenz. Die Eigenfrequenz eines Schwingkreises kann durch die Thomsonsche Schwingungsgleichung berechnet werden:

In dieser Gleichung bedeuten:

• \(\omega_{0}\) Eigenkreisfrequenz des Schwingkreises (in \(\mathrm{1/s}\) oder \(\mathrm{s}^{-1}\))
• \(L\), die Induktivität der Spule (in \(\mathrm{H}\))
• \(C\), die Kapazität des Kondensators (in \(\mathrm{C}/\mathrm{V}\))

Über den Zusammenhang von Kreisfrequenz und Frequenz \(\omega_{0} = 2\pi \cdot f_{0}\) erhalten wir für die Eigenfrequenz:

\[\begin{equation} f_{0} = \frac{\omega_{0}}{2\pi} ={\frac {1}{2\pi\cdot {\sqrt {L\cdot C}}}} \tag{13.53} \end{equation}\]

13.17.3 Herleitung Schwingkreis Eigenfrequenz

In einem Wechselstromkreis mit einem Kondensator gilt für die Effektivwerte:

\[ I_\text{eff} = \omega\cdot C\cdot U_\text{eff} \]

Für eine Spule im Wechselstromkreis gilt für die Effektivwerte:

\[ I_\text{eff} = \frac{1}{\omega\cdot L}\cdot U_\text{eff} \]

Da es keine Verzweigungen gibt, fließt durch beide Bauteile (im Mittel) der gleiche Strom und wir können beide Effektiv-Stromstärken gleichsetzen:

\[ \begin{aligned} \omega\cdot C\cdot U_\text{eff} = {} & \frac{1}{\omega\cdot L}\cdot U_\text{eff} &&\qquad\Bigr\rvert\cdot \frac{1}{U_\text{eff}} \\ \omega\cdot C = {} & \frac{1}{\omega\cdot L} &&\qquad\Bigr\rvert\cdot \frac{\omega}{C} \\ \frac{\omega^2\cdot \cancel{C}}{\cancel{C}} = {} & \frac{\cancel{\omega}}{\cancel{\omega}\cdot L\cdot C} \\ \omega^2 = {} & \frac{1}{L\cdot C} &&\qquad\Bigr\rvert\;\sqrt{(...)}\\ \omega = {} & \frac{1}{\sqrt{L\cdot C}}\\ \end{aligned} \]

13.17.4 Schwingkreis und mechanischer Oszillator

In Bild 13.209 siehst du den Vergleich eines elektrischen Schwingkreises mit einem Federpendel.

Bild 13.209: Vergleich eines Schwingkreises mit einem Federpendel

• Zu Beginn ist die gesamte Energie als potenzielle Energie in der Feder (\(E_\text{pot}\)) gespeichert. Das entspricht der elektrischen Feldenergie (\(E_\text{el}\)) des geladenen Kondensators.

\[ E_\text{spann}=\frac{k\cdot x^2}{2}\qquad E_\text{el} = \frac{C\cdot U^2}{2} \]

• Die Elongation der Feder entspricht der momentanen Ladung auf dem Kondensator und der Federspannung der elektrischen Spannung am Kondensator.

• Die Federkonstante \(k\) beim Federpendel entspricht der Kapazität \(C\) des Kondensators.

• Der Pendelkörper beschleunigt und erreicht seine Maximalgeschwindigkeit. Zu diesem Zeitpunkt steckt die gesamte Energie in der kinetischen Energie des Pendelkörpers (\(E_\text{kin}\)). Das entspricht der magnetischen Feldenergie (\(E_\text{mag}\)) der Spule.

\[ E_\text{kin}=\frac{m\cdot v^2}{2}\qquad E_\text{mag} = \frac{L\cdot I^2}{2} \]

• Die Trägheit (Masse) \(m\) im mechanischen Oszillator entspricht der Induktivität \(L\) der Spule.

• Die Geschwindigkeit \(v\) des Pendelkörpers entspricht der Stromstärke \(I\) im Schwingkreis.

Durch die Ähnlichkeit der beiden Systeme lassen sich viele Erkenntnisse aus den mechanischen Schwingungen (gedämpfter Oszillator, Resonanz,…) auf Schwingkreise übertragen.

13.17.5 Realer Schwingkreis

Jeder reale Bauteil besitzt einen gewissen ohmschen Widerstand. Fließt Strom, wird immer ein Teil der Energie als Wärme an die Umgebung abgegeben (Dissipation). Ein realer Schwingkreis verliert daher bei jedem Zyklus an Energie. Er verhält sich dabei wie ein gedämpfter, mechanischer Oszillator.

Bild 13.210: Stromkurve eines realen Schwingkreises

Am Oszilloskop kannst du eine exponentiell abklingende Kurve beobachten, auf der die Spitzenwerte der oszillierenden Stromstärke liegen (strichlierte Kurve in Bild 13.210) liegen.

13.17.6 Resonanzverhalten eines Schwingkreises

Wir wählen wieder einen Schwingkreis mit genügend kleinem ohmschen Widerstand, sodass wir diesen vernachlässigen können. Dieses Mal überlassen wir ihn nicht sich selbst, sondern führen mit einer Wechselspannungsquelle (etwa einem Frequenzgenerator) periodisch Energie zu (Bild 13.211).

Bild 13.211: Angetriebener Schwingkreis

Wie bei einem mechanischen Oszillator können wir dem Schwingkreis damit jede beliebige Frequenz „aufzwingen“. Je nach anregender Frequenz \(f\) verhält sich der Schwingkreis aber unterschiedlich (Bild 13.212).

Bild 13.212: Blindstrom bei unterschiedlicher Anregungsfrequenz

Bei niedriger Anregungsfrequenz (\(f < f_0\)) ist der induktive Widerstand klein und damit \(I_\text{L, eff}\) groß. Umgekehrt ist der kapazitive Widerstand bei kleinen Frequenzen groß, \(I_\text{C, eff}\) damit klein. Da wir den ohmschen Widerstand vernachlässigen, erhalten wir für den Betrag des (Blind-)Stromes \(I_\text{eff} = |I_\text{L, eff}-I_\text{C, eff}|\).

Erhöhen wir die anregende Frequenz, wird \(I_\text{L, eff}\) immer kleiner und \(I_\text{C, eff}\) immer größer. Erreichen wir schließlich die Eigenfrequenz des Schwingkreises (\(f = f_0\)), tritt Resonanz auf. In diesem Fall heben die beiden Blindströme einander auf und es gibt in den Zuleitungen (fast) keinen Strom mehr. Liegt die Anregefrequenz über der Resonanzfrequenz (\(f > f_0\)), wird \(I_\text{C, eff}\) jetzt größer als \(I_\text{L, eff}\) und wir erhalten wieder einen (Blind-)Strom \(I_\text{eff}\).