13.19 Elektromagentische Wellen
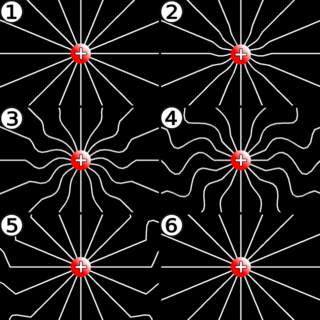
Nachdem James Clerk Maxwell mit seinen Gleichungen die Entstehung von elektromagnetischen Wellen vorausgesagt hatte, konnte Heinrich Hertz 1886 als Erster elektromagnetische Wellen experimentell nachweisen (Bild 13.227) und in einer Reihe von Experimenten ihre Welleneigenschaften (unter anderem Reflexion, Brechung, Beugung) nachweisen. Demonstrationsversuche zu Welleneigenschaften von elektromagnetischen Wellen werden bis heute Hertzsche Versuche genannt.
In diesem Kapitel wirst du erfahren, wie eine Antenne funktioniert, wie diese mit einem elektrischen Schwingkreis zusammenhängt und wie es zur Entstehung von elektromagnetischen Wellen kommt.
13.19.1 Störung im elektrischen Feld
In Bild 13.228 siehst du das Feldlinienbild des elektrischen Feldes einer Ladung. Wird die Ladung kurz (sinusförmig) bewegt, wirkt sich diese Änderung nicht sofort auf den gesamten Raum aus. Stattdessen breitet sich die Information über die Ortsänderung der Ladung verzögert aus. Es entsteht eine Störung im elektrischen Feld, die sich wellenförmig im Raum ausbreitet.
Jede beschleunigte elektrische Ladung verursacht eine Störung im elektrischen Feld, die sich mit großer, aber endlicher Geschwindigkeit (Lichtgeschwindigkeit) im Raum ausbreitet.
13.19.2 Offener Schwingkreis
Wir gehen von einem LC-Schwingkreis aus und nehmen einige Veränderungen vor (Bild 13.229 1). Zunächst biegen wir den Kondensator auf (2-3), verkleinern die Kondensatorplatten (4) und reduzieren die Windungszahl der Spule (5) und ziehen sie zu einem geraden Leiter in die Länge (6).
Rein optisch hat der gerade Leiter recht wenig mit unserem ursprünglichen Schwingkreis gemeinsam. Aber jeder Leiter kann elektrische Ladungen aufnehmen und besitzt daher eine gewisse Kapazität. Da auch ein gerader stromdurchflossener Leiter ein Magnetfeld erzeugt, besitzt er auch eine gewisse Induktivität. Damit ist auch ein gerades Leiterstück ein vollständiger Schwingkreis! Er wird als offener Schwingkreis (engl. dipole antenna) bezeichnet.
Im Gegensatz zu unserem ursprünglichen Schwingkreis ist die Kapazität des geraden Leiters sehr klein, weil sie proportional zur Fläche der Kondensatorplatten ist. Ebenso die Induktivität, die proportional zur Querschnittsfläche und der zweiten Potenz der Windungszahl einer Spule ist. Durch den Umbau erhalten wir nach der Thomsonsche Schwingungsgleichung also einen Schwingkreis mit extrem hoher Eigenfrequenz, der durch seine Länge bestimmt ist.
13.19.3 Halbwellendipol
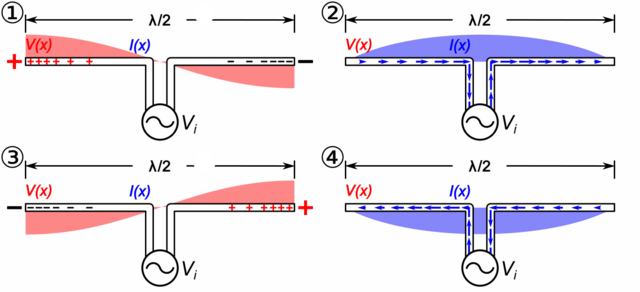
In Bild 13.230 siehst du einen offenen Schwingkreis, der mithilfe einer Wechselspannungsquelle mit seiner Eigenfrequenz angeregt wird.
Die Wechselspannung verschiebt die Elektronen abwechselnd an das linke und das rechte Ende. Der Leiter bildet dabei einen elektrischen Dipol mit wechselnder Polarität. Der Stromfluss in der Mitte des Leiters ändert ständig seine Größe, bleibt aber an den Enden immer null. Sowohl Strom als auch Spannung bilden eine stehende Welle. Für den Strom entspricht das dem Fall einer mechanischen stehenden Welle bei einer Saite mit zwei festen Enden bei der Spannung dem Fall von zwei offenen Enden. In beiden Fällen ist die Länge des Leiters genau die Hälfte der Wellenlänge \(\lambda\), daher die Bezeichnung Halbwellendipol (oder \(\lambda/2\)-Dipol, engl. half-wave dipole).
13.19.4 Abstrahlung eines Halbwellendipols
Im Gegensatz zu einem geschlossenen Schwingkreis ist ein offener Schwingkreis in der Lage, eine elektromagnetische Welle „abzustrahlen“ – daher: Die Feldänderungen sind auch in größerer Entfernung vom Schwingkreis noch messbar.
In Bild 13.231 siehst du die Änderung des elektrischen Feldes, die durch einen sinusförmig angeregten offenen Schwingkreis verursacht wird.
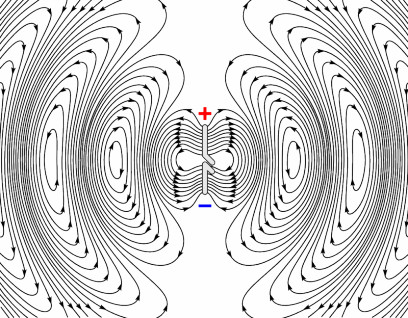
In Bild 13.232 siehst du zusätzlich zu dem elektrischen Feld E auch die Feldlinien des magnetischen Feldes B. An der Schnittachse der beiden Ebenen siehst du auch noch die Feldstärken-Vektoren von elektrischem und magnetischem Feld eingezeichnet.
Links:
- WebApp: Dipolstrahlung
13.19.5 Nah- und Fernfeld
Betrachten wir die Felder eines Halbwellendipols etwas genauer. In unmittelbarer Nähe (Nahfeld, engl. near field) wechseln sich magnetisches und elektrisches Feld ab. Befinden sich die Elektronen an einem Stabende (maximales elektrisches Feld), gibt es keinen Stromfluss und das magnetische Feld ist null und umgekehrt. Das elektrische und das magnetisches Feld sind zeitlich also um eine Viertelperiode verschoben. In diesem Bereich ist die elektrische Feldstärke – wie beim statischen Dipol – proportional zu \(1/r^3\), nimmt also mit der dritten Potenz des Abstandes ab.
Entfernen wir uns etwa eine Wellenlänge vom offenen Schwingkreis, ändern sich die Verhältnisse (Bild 13.233) deutlich. In diesem Fernfeld (engl. far field) stellen wir fest:
die elektrischen Feldlinien sind geschlossen (elektrische Wirbelfelder, Bild 13.231)
elektrisches und magnetisches Feld sind in Phase – die Phasenverschiebung ist null.
die elektrische als auch die magnetische Feldstärke nehmen nur mehr linear mit dem Abstand \(r\) zum Sender ab.
\[ B\propto E \propto \frac{1}{r} \]
Wie können wir die verminderte Abnahme des Fernfeldes verstehen? Von den Maxwell-Gleichungen wissen wir:
- Durch ein zeitlich veränderliches elektrisches Feld wird ein zeitlich veränderliches Magnetfeld induziert (Erweiterte Durchflutungsgesetz)
- Durch ein zeitlich veränderliches Magnetfeld wird ein zeitlich veränderliches elektrisches Feld induziert (Faradaysches Induktionsgesetz)
Im Fernfeld erzeugen sich elektrisches Feld und Magnetfeld also gegenseitig und halten sich auf diese Weise sozusagen länger „am Leben“.
Das Fernfeld ist das, was wir als elektromagnetische Strahlung bezeichnen. Es ist unabhängig von den elektrischen Ladungen im Sender. Das bedeutet, dass eine Änderung des Fernfeldes keine Rückwirkung auf den Sender hat. Daher muss ein Radiosender seine Leistung nicht erhöhen, wenn mehr Radios das Signal empfangen. Einmal abgestrahlt, ist die elektromagnetische Welle vollkommen unabhängig von ihrer Quelle.
13.19.6 Ausbreitung elektromagnetischer Wellen
In Bild 13.234 siehst du die Ausbreitung einer elektromagnetischen Welle oder EM-Welle (engl. electromagnetic wave) in großer Entfernung von der Sende-Antenne.
An jeder Stelle der Welle ändern sich der elektrische Feldvektor \(\vec{E}\) und der magnetische Anteil \(\vec{B}\) periodisch und phasengleich. Beide Feldvektoren stehen im rechten Winkel zueinander und schwingen normal zur Ausbreitungsrichtung der Welle. Bei einer elektromagnetischen Welle handelt es sich also um eine Transversalwelle, die sich mit Lichtgeschwindigkeit \(c\) ausbreitet.
Elektromagnetische Wellen verhalten sich in vielen Fällen wie mechanische Wellen. Sie weisen Beugung, Interferenz, Reflexion und Brechung auf. Ebenso wie eine mechanische Welle transportieren elektromagnetische Wellen Energie. Einen wichtigen Unterschied gibt es aber: Im Gegensatz zu mechanischen Wellen benötigt eine elektromagnetische Welle kein Medium zur Ausbreitung!
13.19.7 Energiefluss-Vektor
Der Transport der Energie erfolgt immer entlang der Ausbreitungsrichtung einer elektromagnetischen Welle. Sie kann in Vakuum oder Luft daher durch eine Größe beschrieben werden, die aus dem Kreuzprodukt der beiden Feldvektoren (\({\vec {E}}\times {\vec {B}}\)) gebildet wird. Dieser Energiefluss-Vektor oder Poynting-Vektor \(\vec{S}\) (benannt nach John Henry Poynting) steht in jedem Punkt senkrecht auf den elektrischen und magnetischen Feldvektor.
Die Richtung kannst du dir mit der 3-Finger-Regel für die rechte Hand (EBS-Regel) überlegen. Beginne – so wie beim Zählen mit den Fingern – mit dem Daumen:
- E-Feldvektor (Daumen),
- B-Feldvektor (Zeigefinger) und
- Energiefluss-Vektor (Mittelfinger).
Für den Poynting-Vektor gilt der Satz von Poynting, der den Energieerhaltungssatz für elektromagnetische Felder ausdrückt.
13.19.8 Winkelabhängigkeit der Abstrahlung
In Richtung der Sende-Antenne gibt es keine Feldänderung und daher auch keine Abstrahlung. Die größte Feldänderung (und damit die maximale Abstrahlung) erfolgt beim Halbwellendipol in der Ebene im rechten Winkel zur Antenne. In den Winkeln dazwischen kommt es aber ebenfalls zu einer Abstrahlung.
In Bild 13.236 siehst du die Intensität (das Amplitudenquadrat) der abgestrahlten elektromagnetischen Welle in Abhängigkeit vom Winkel.
13.19.9 Empfang durch einen Dipol
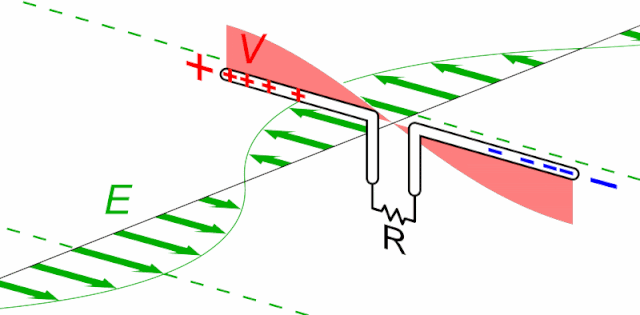
Befinden sich Ladungsträger in einem elektrischen Wechselfeld, werden sie zu einer Schwingung angeregt (Bild 13.237, der magnetische Anteil der Welle wurde aus Übersichtsgründen weggelassen).
Damit die elektrische Kraft auf die Elektronen zu einer maximalen Bewegung führt, muss der Leiter entlang des elektrischen Feldvektors \(\vec{E}\) ausgerichtet sein – daher parallel zur Sende-Antenne (Bild 13.238). Ist die Länge des Leiters auf die Wellenlänge der elektromagnetischen Welle abgestimmt (\(\ell = \lambda/2\)), tritt außerdem Resonanz auf und selbst bei einer schwachen elektromagnetischen Welle kommt es zu einer ausgeprägten Schwingung in der Empfangsantenne.
13.19.10 Reflektordipol
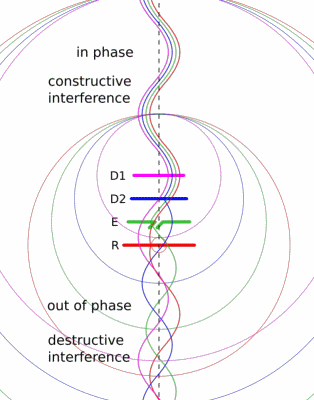
Bei einem Halbwellendipol ist die Abstrahlung nach allen Seiten gleich groß. Es gibt aber auch Tricks, wie die Abstrahlung oder der Empfang von einer Antenne in eine bestimmte Richtung vergrößert werden kann. Eine Möglichkeit ist die Verwendung eines Reflektordipols wie bei der Yagi-Uda-Antenne (engl. Yagi–Uda antenna, Bild 13.239).
Sie besteht neben der eigentlichen Antenne A (Halbwellendipol) aus einem Reflektor R und ein oder mehreren Direktorstäben D. Während die Antenne aktiv mit einer Spannung versorgt wird, werden Reflektor und die Direktorstäbe passiv durch das Feld der Antenne zu Schwingungen angeregt. Der Abstand des Reflektors ist mit \(\lambda/4\) zum Sende-Dipol gerade so gewählt, dass dort eine gegenphasige Welle erzeugt wird und sich die Welle hinter der Antenne durch destruktive Interferenz auslöschen. Die Abstände der Direktorstäbe sind so gewählt, dass sich die Wellen vor der Antenne durch konstruktive Interferenz verstärken (Bild 13.240).
13.19.11 Energieübertragung bei einem einfachen Stromkreis
Im Kapitel über Stromkreise hast du viel über die Verhältnisse von Stromstärke und Spannung kennengelernt. Wie aber genau die Energieübertragung in einem Stromkreis funktioniert, wurde nicht besprochen. Das wollen wir jetzt nachholen. In Bild 13.241 ist zunächst ein offener Stromkreis mit einer Batterie zu sehen.
Es fließt kein Strom, aber die Spannungsquelle sorgt dafür, dass es zu einem Elektronenüberschuss auf der Leiteroberfläche des mit dem negativen Batteriepol verbundenen Drahtes kommt. Umgekehrt herrscht auf der Leiteroberfläche des Drahtes, der mit dem positiven Batteriepol verbunden ist, ein Elektronenmangel. Die Leitungen verhalten sich wie ein Kondensator, der aus zwei sehr dünnen, langen „Kondensatorplatten“ besteht. Zwischen den beiden Leitern entsteht ein dauerhaftes elektrisches Feld (blaue Feldvektoren).
Bild 13.242: Energieübertragung durch das elektromagnetische Feld bei einem geschlossenen Gleichstromkreis
Schließen wir den Stromkreis (Bild 13.242), indem wir einen Widerstand einfügen, erhalten wir zusätzlich zu dem elektrischen Kondensatorfeld der Drähte, ein magnetisches Feld, das durch den Stromfluss im Inneren der Drähte hervorgerufen wird (rote Feldvektoren). Die Energiefluss-Vektoren zeigen jeweils in die Richtung des Kreuzproduktvektors von \(\vec{E}\) und \(\vec{B}\). Sie sind als gelbe Pfeile im Bild zu erkennen. Die Energiefluss-Vektoren zeigen von der Spannungsquelle weg – Energie fließt hier aus der Batterie in das elektromagnetische Feld. Im Bereich um den Widerstand sind sie nach innen gerichtet – Energie wird aus dem Feld aufgenommen und in Wärme umgewandelt. Im Bereich dazwischen findet die Übertragung der Energie hauptsächlich im Feld in der Nähe der Leiter statt.
Verwendest du statt einer Gleichspannungsquelle eine Wechselspannungsquelle, macht das für die Energieübertragung keinen Unterschied. Mit der Spannung wechselt die Stromrichtung, ebenso wie die Polarität des Draht-Kondensators. Der Energiefluss-Vektor ändert dabei nie die Richtung.
Vielleicht hast du gedacht, dass die Energie von der Spannungsquelle nur durch die Drähte transportiert wird. Auch wenn die meiste Energie in der Nähe der Drähte übertragen wird, ist doch das gesamte elektromagnetische Feld zwischen Spannungsquelle und Verbraucher an der Übertragung der Energie beteiligt! Betreibst du ein Elektrogerät bei dir daheim, ist das gesamte elektromagnetische Feld zwischen dem Kraftwerk und deinem Zuhause für die Energieübertragung verantwortlich. Wahnsinn, oder?
