9.4 Stehende Wellen
In Kapitel Ausbreitung von Wellen hast du die Überlagerung von Wellen kennengelernt und im Kapitel über begrenzte Wellenmedien über die Reflexion von Wellen.
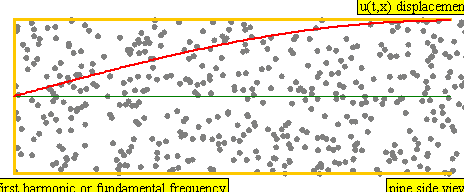
In diesem Kapitel werden wir das Wissen aus beiden Kapiteln zusammenführen und uns mit stehenden Wellen beschäftigen (Bild 9.27).
9.4.1 Stehende Welle
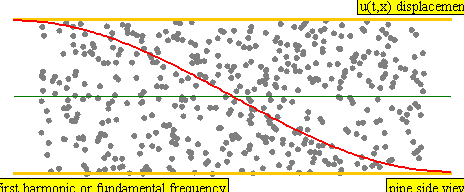
Überlagern sich zwei in entgegengesetzter Richtung laufende Wellen mit gleicher Frequenz (Wellenlänge), entsteht eine stehende Welle (engl. standing wave).
In der überlagerten Welle (Bild 9.28) ist keine Ausbreitungsrichtung erkennbar. Du kannst Stellen ohne Bewegung ( Wellenknoten (engl. nodes)) (grüne Punkte) und Stellen maximaler Bewegung ( Wellenbäuche (engl. antinodes)) erkennen.
Links:
- Video: Stehende Wasserwellen
9.4.2 Eigenschwingungen bei zwei festen Enden
In einem begrenzten Medium mit zwei festen Enden (zum Beispiel einer Saite auf einem Saiteninstrument) überlagert sich eine angeregte Welle mit seinen Reflexionen. Bei der Anregung mit bestimmten Frequenzen ergibt sich dabei eine stehende Transversalwelle. Diese Frequenzen werden Eigenschwingungen (engl. modes) der Saite genannt. Die Eigenschwingung mit der kleinsten Frequenz wird als Grundschwingung (engl. fundamental frequency) bezeichnet, alle anderen werden Oberschwingungen (engl. overtones) genannt.
Da sich die Saite an den Enden nicht bewegen kann, müssen sich an diesen beiden Stellen immer Wellenknoten der stehenden Welle befinden.
In Bild 9.29 siehst du die ersten drei Eigenschwingungen einer Saite. Im einfachsten Fall gibt es nur zwei Schwingungsknoten, jeweils am Anfang und am Ende der Saite. In diesem Fall ist die Länge \(L\) der Saite gerade eine halbe Wellenlänge lang.
\[ L = \lambda\cdot 1/2 \]
Für drei Knoten entlang der Saite ist die Wellenlänge genau die Länge der Saite (oder zwei halbe Wellenlängen).
\[ L = \lambda\cdot 2/2 \]
Allgemein gilt für die \(n\)-te Eigenschwingung die Beziehung:
| \[\begin{equation} L = \lambda\cdot n/2 \qquad n=1,2,3,4,\ldots \tag{9.3} \end{equation}\] |
Im selben Verhältnis, wie die Wellenlängen \(\lambda\) für die Oberschwingungen abnehmen, nehmen die Frequenzen zu. In dem Hörbeispiel Audio abspielen werden der Grundton (\(110\;\mathrm{Hz}\)) und die ersten 16 Obertöne der Reihe nach gespielt (\(220\;\mathrm{Hz}\), \(330\;\mathrm{Hz}\), \(440\;\mathrm{Hz}\),…).
Links:
9.4.3 Eigenschwingungen bei einem festen und einem losen Ende
Die Flöten einer Panflöte sind an einem Ende offen, am anderen Ende geschlossen (gedeckte Pfeife). Mit der Länge \(L\) einer Flöte entsteht damit ein begrenztes Wellenmedium mit einem festen und einem offenen Ende. Bei der Anregung mit bestimmten Frequenzen ergibt sich dabei eine stehende Longitudinalwelle. Die Luftbewegung für die Grundschwingung siehst du in Bild 9.30
Schwingungsknoten einer Luftsäule entsprechen den Stellen, an denen sich die Luftmoleküle nicht bewegen. Die Schwingungsbäuche entsprechen den Stellen in der Luftsäule, an denen sich die Luftmoleküle maximal bewegen.
In der Grundschwingung erkennen wir ein Viertel der Wellenlänge. Daher gilt:
\[ L = \lambda\cdot 1/4 \]
Fügen wir einen Schwingungsknoten hinzu, entspricht das der ersten Oberschwingung (Bild 9.31, 2). Die dunklen Stellen zeigen die Schwingungsknoten an.
Die Länge des Wellenmediums entspricht jetzt dreiviertel einer Wellenlänge
\[ L = \lambda\cdot 3/4 \]
Allgemein gilt für die \(n\)-te Eigenschwingung die Beziehung:
| \[\begin{equation} L = \lambda\cdot\frac{2n-1}{4} \qquad n=1,2,3,4,\ldots \tag{9.4} \end{equation}\] |
Wenn du normal eine Flöte anbläst, hörst du immer die Grundschwingung. Wenn du sehr kräftig die Flöte anbläst, kommt es zur Anregung mit der zweiten Eigenschwingung. Diese Technik wird Überblasen genannt. Beachte, dass die Frequenz der ersten Oberschwingung nicht das Doppelte der Grundschwingung ist. Der überblasene Ton einer Panflötenpfeife ist eine Duodezime höher als ihr Grundton.
Links:
9.4.4 Kundtsches Staubrohr
Luftmoleküle können wir nicht sehen, weil sie so klein sind. Trotzdem gibt es Möglichkeiten, eine stehende Schallwelle sichtbar zu machen, wie zum Beispiel mithilfe des Kundtschen Staubrohrs (engl. Kundt’s tube, benannt nach August Kundt). Es besteht aus einer offenen luftgefüllten Glasröhre, deren hinteres Ende mit einem Stempel verschlossen ist (Bild 9.32). Durch Verschieben des Stempels kann die Länge der Luftsäule verändert werden.
Zunächst wird ein feines Pulver (etwa Korkmehl oder Bärlappsporen) in die Röhre gegeben und anschließend die Luftsäule mithilfe eines Lautsprechers in Schwingung versetzt. Ist die Länge der Luftsäule so gewählt, dass sich eine stehende Schallwelle bildet, sammelt sich das Pulver an den Knotenpunkten - also an den Stellen, wo die Luft nicht schwingt. Die Wellenlänge \(\lambda\) kann dann als Entfernung zum übernächsten Knotenpunkt bestimmt werden. Ist außerdem die anregende Schallfrequenz \(f\) bekannt, kann mithilfe der Grundgleichung der Wellenlehre die Schallgeschwindigkeit berechnet werden:
\[ c = \lambda\cdot f \]
9.4.5 Rubenssches Flammenrohr
Ein ähnliches aber weitaus spektakuläreres Experiment zur Veranschaulichung einer stehenden Schallwelle ist das Rubenssche Flammenrohr (engl. Rubens tube, benannt nach Heinrich Rubens), das du vom Kapitelanfang kennst. Im Gegensatz zum Kundtschen Staubrohr ist das Rohr aus Metall und hat viele kleine Bohrungen auf der Oberseite. In das Rohr wird ein brennbares Gas eingeleitet und an den Löchern entzündet. Durch einen Lautsprecher auf einer Seite des Rohres wird das Gas in Schwingung versetzt. Kann sich eine stehende Welle ausbilden, ist das an den „Flammenhügeln“ zu erkennen, die in regelmäßigen Abstanden auftreten.
Bewegst du eine brennende Kerze schnell hin und her, geht sie aus. So ähnlich ist es auch beim Flammenrohr: An den Stellen, wo sich die Luft heftig hin- und herbewegt, gehen die Flammen aus. Dort befinden sich Schwingungsbäuche. Umgekehrt befinden sich Schwingungsknoten (nicht schwingende Luft) an den Stellen, an denen die Flamme hoch und ruhig brennt (Bild 9.33).
9.4.6 Eigenschwingungen bei zwei losen Enden
Eine Blockflöte ist ein Beispiel für eine auf beiden Seiten offene Flöte. Mit der Länge \(L\) der Flöte entsteht damit ein begrenztes Wellenmedium mit zwei offenen Enden. Bei der Anregung mit bestimmten Frequenzen ergibt sich dabei eine stehende Longitudinalwelle. Die Luftbewegung für die Grundschwingung siehst du in Bild 9.34
In der Mitte der Flöte befindet sich ein Schwingungsknoten. In der Grundschwingung kannst du eine halbe Wellenlänge entdecken. Daher gilt:
\[ L = \lambda\cdot 1/2 \]
Fügen wir einen Schwingungsknoten hinzu, entspricht das der ersten Oberschwingung (Bild 9.35, 2). Die dunklen Stellen zeigen die Schwingungsknoten an.
Die Länge des Wellenmediums entspricht jetzt genau einer Wellenlänge, also:
\[ L = \lambda\cdot 2/2 \]
Allgemein gilt für die \(n\)-te Eigenschwingung die Beziehung:
| \[\begin{equation} L = \lambda\cdot n/2 \qquad n=1,2,3,4,\ldots \tag{9.5} \end{equation}\] |
Also genau dieselben Beziehungen wie bei zwei festen Enden. Wenn du normal eine Flöte anbläst, hörst du immer die Grundschwingung. Wenn du sehr kräftig die Flöte anbläst, kommt es zur Anregung mit der zweiten Eigenschwingung. Diese Technik wird Überblasen genannt. Da die Frequenz der Oberschwingung immer genau das Doppelte der vorherigen Schwingung ist, erhältst du durch Überblasen bei der Blockflöte einen um eine Oktave höheren Ton.
Das Flammenrohr am Kapitelanfang (Bild 9.27) ist ebenfalls ein Beispiel für eine stehende Welle in einem Rohr mit zwei offenen Enden. Die Lautsprechermembranen bilden den Abschluss auf beiden Seiten des Rohrs. Da sie sich bewegen, müssen sich dort Schwingungsbäuche befinden. Bewegst du eine brennende Kerze schnell hin und her, geht sie aus. Das Gleiche gilt für das Flammenrohr. An den Stellen, an denen sich die Luft heftig hin- und herbewegt (Schwingungsbäuche) gehen die Flammen aus. Umgekehrt befinden sich die Schwingungsknoten (unbewegte Luft) an den Stellen, an denen die Flamme hoch und ruhig brennt.
9.4.7 Zweidimensionale Eigenschwingungen
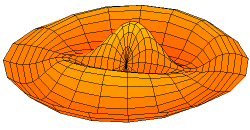
Die Schwingungsmembran einer Trommel ist ein Beispiel für ein zweidimensionales, begrenztes Wellenmedium. Die hier möglichen stehenden Wellen (Eigenschwingung) hängen nicht nur von Größe, sondern auch von der geometrischen Form der Membran (Kreis, Rechteck,…) ab. Statt Knotenpunkten treten hier Knotenlinien auf. In Bild 9.36 siehst du ein Beispiel für so eine zweidimensionale stehende Welle.
Mitte des 18. Jahrhunderts hat der deutsche Physiker Ernst Chladni (ausgesprochen wie „klad-ni“) eine sehr einfache Methode gefunden, die Knotenlinien von stehenden Wellen einer Membran sichtbar zu machen. Dabei werden auf fix montierte Metallplatten Sand gestreut und anschließend mit einem Geigenbogen seitlich zum Schwingen gebracht. Der Sand sammelt sich an den Knotenlinien, wo die Membran keine Bewegung ausführt, und es entstehen die charakteristischen Chladnische Klangfiguren (Bild 9.37).
Links:
9.4.8 Stimme
In deinem Hals befinden sich zwei v-förmig angeordnete elastische Stimmbänder (engl. vocal cords), die sogenannten Stimmlippen (Bild 9.38). Beim Sprechen oder Singen werden diese Bänder durch die ausströmende Luft aus deiner Lunge wie eine Saite mit zwei festen Enden zu Schwingungen angeregt.
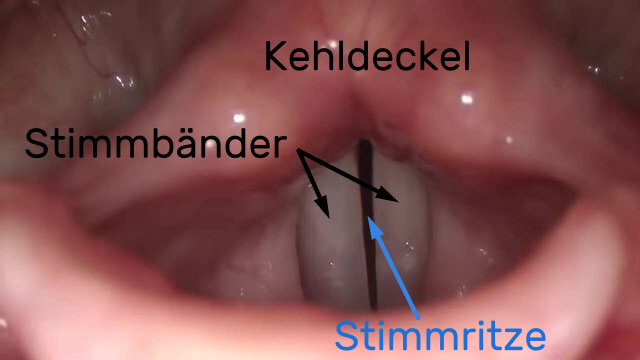
Bild 9.38: Blick in den Kehlkopf: Links und rechts von der Stimmritze (Spalt) befinden sich die Stimmbänder
Die Länge der Stimmbänder beträgt bei einem erwachsenen Mann rund \(2\;\mathrm{cm}\), bei Frauen nur etwa \(1{,}5\;\mathrm{cm}\). Durchschnittlich ist eine Frauenstimme damit um rund eine halbe Oktave höher als eine Männerstimme. Deinen Grundton hörst du dann, wenn du ein entspanntes „Mhhh“ oder „Ommm“ (die heilige Silbe der Hindus) summst. Durch die Muskulatur in deinem Kehlkopf kannst du die Spannung deiner Stimmbänder erhöhen und so auch höhere Töne erzeugen (Bild 9.39). Der durch die Stimmbänder entstandene Ton wird durch deine Hohlräume im Brustkorb und Kopf (Mundhöhle, Rachen, Nasenhöhle, Kieferhöhlen, Keilbeinhöhle) verändert. Weil diese bei jedem Menschen leicht unterschiedlich gewachsen sind, ist deine Stimme so eindeutig wie ein Fingerabdruck. Aber auch die Position deiner Zunge, die Stellung deines Kiefers oder die Form deiner Lippen ändern den Hohlraum und damit den Ton. Das ermöglicht uns, eine Vielzahl an unterschiedlichen Lauten zu erzeugen.
Durch eine bestimmte Stellung des Kehlkopfes erreichen trainierte Sängerinnen und Sänger eine noch höhere Spannung der Stimmbänder. Dies gestattet ihnen, in einer höheren Stimmlage zu singen. Diese Technik wird Falsett oder Kopfstimme genannt und entspricht der Technik des Überblasens bei einem Blasinstrument.
In der Pubertät erlebt fast jeder von uns eine Veränderung der Stimme (Stimmwechsel oder Stimmbruch). Die Stimmlippen werden dicker und fester und der Kehlkopf größer und fester. Bei Männern tritt der Kehlkopf dabei deutlicher hervor (Adamsapfel). Diese Veränderung lässt die Stimme um bis zu einer Oktave tiefer werden.
Die meisten Menschen sind sehr überrascht, wenn sie das erste Mal eine Aufnahme ihrer eigenen Stimme hören. Sie klingt ganz anders als die Stimme, die sie selbst wahrnehmen. Das liegt daran, dass die Schallschwingungen deiner Stimme nicht nur von Außen an dein Ohr dringen, sondern zusätzlich von Innen durch den Schädelknochen an dein Hörorgan geleitet werden. Da durch Körperschall besonders tiefe Frequenzen gut übertragen werden, hörst du deine eigene Stimme immer etwas tiefer.