9.1 Entstehung von Wellen
Durch das zeitversetzte Aufstehen der Zuschauer in einem Stadion entsteht eine beeindruckende La-Ola-Welle (Bild 9.2)
Ist diese Erscheinung aber schon eine Welle nach der physikalischen Definition?
Links:
- Applet: Einführung Wellen
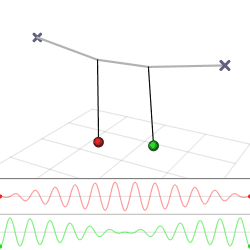
9.1.1 Gekoppelte Pendel
Zwei Fadenpendel mit derselben Länge werden mit einer Gummischnur in der Mitte verbunden (gekoppelt). Eines der Fadenpendel wird ausgelenkt und losgelassen (Bild 9.3). Die Anordnung wird gekoppelte Pendel (engl. coupled oscillators) genannt.
Durch die Koppelung übt das angeregte Pendel eine periodische Kraft auf das noch ruhende Pendel aus. Da beide Pendel dieselbe Fadenlänge haben, besitzen beide Pendel dieselbe Eigenfrequenz. Durch diesen Resonanzfall überträgt sich die Schwingungsenergie allmählich vollständig auf das zweite Pendel. Jetzt vertauschen beide Pendel ihre Rollen und das zweite Pendel überträgt seine Schwingungsenergie wieder auf das erste Pendel. Die Energie wandert periodisch zwischen beiden Pendeln hin und her. Je schwächer die Kopplung, desto langsamer wird die Energie übertragen.
9.1.2 Definition Welle
Können Oszillatoren Kraft auf benachbarte Oszillatoren ausüben (gekoppelte Oszillatoren), können sich Schwingungen räumlich ausbreiten und eine Welle entsteht. Die allgemeinste Definition einer Welle (engl. wave) in der Physik ist diese:
| Eine Welle ist eine sich räumlich ausbreitende Störung. |
Ist die Störung periodisch, entsteht eine sich ausbreitende Schwingung. Diese Definition einer Welle gilt sowohl für mechanische Wellen als auch für elektromagnetische Wellen, die du in einem späteren Teil des Buches kennenlernen wirst.
9.1.3 Wellenmedium
Alle mechanischen Wellen benötigen ein Medium, in dem sie sich ausbreiten können, ein sogenanntes Wellenmedium. Ein Wellenmedium besteht aus einer Reihe von Oszillatoren, die untereinander verbunden sind. Durch diese Kopplung kann ein Oszillator auf seinen Nachbarn Kraft ausüben (Kopplungskräfte) und seine Bewegung übertragen. Jeder Oszillator bewegt sich dabei immer nur um seine Ruhelage.
| Bei einer Welle wird immer nur Energie räumlich übertragen, aber kein Material (Masse) transportiert. |
Jeder einzelne Oszillator des Wellenmediums führt dabei dieselbe Schwingung aus. Da die Übertragung der Kraft durch die Koppelung Zeit kostet, schwingen die Oszillatoren nicht alle gleichphasig, sondern zeitversetzt. Je nach Schwingungsrichtung der Oszillatoren lassen sich die folgenden Wellentypen unterscheiden:
- Transversalwelle
- Longitudinalwelle
- Kreiswelle
9.1.4 Transversalwelle
Bewegen sich die einzelnen Oszillatoren des Wellenmediums senkrecht zur Ausbreitungsrichtung der Welle, wird von einer Transversalwelle oder Querwelle (engl. transverse wave) (interaktives Bild 9.4) gesprochen. Dabei wechseln Wellentäler und Wellenberge einander ab.
Die Oszillatoren können nur durch ein Gitter Kräfte normal zur Bewegungsrichtung an ihre benachbarten Oszillatoren weitergeben (Schubkräfte). Daher ist die Ausbreitung von Transversalwellen nur in Festkörpern möglich.
9.1.5 Longitudinalwelle
Bei einer Longitudinalwelle oder Längswelle (engl. longitudinal wave) bewegen sich die einzelnen Oszillatoren des Wellenmediums in Ausbreitungsrichtung der Welle (interaktives Bild 9.5). Dabei wechseln Verdünnungen und Verdichtungen einander ab.
Drehst du die Oszillatoren einer transversalen Welle mit der gleichen Amplitude um \(90^\circ\) im Uhrzeigersinn um ihre Ruhelage (Bild 9.6), erhältst du die Verdichtungen (a) und Verdünnungen (b) einer longitudinalen Welle.
Die Übertragung von Bewegungsenergie in Bewegungsrichtung auf benachbarte Oszillatoren kann durch ein Gitter als auch durch direkten Stoß erfolgen. Daher sind Longitudinalwellen in Festkörpern, Flüssigkeiten und Gasen möglich.
9.1.6 Kreiswelle
Die Kreiswelle (engl. surface wave) ist eine Mischung aus Transversal- und Longitudinalwelle (interaktives Bild 9.7).
Sie tritt an der Oberfläche von Flüssigkeiten und Festkörpern auf.
9.1.7 Welleneigenschaften
In Bild 9.8 siehst du das Foto einer Transversalwelle. Du kannst eine Welle – im Gegensatz zu einer Schwingung – fotografieren, weil es sich bei einer Welle um ein räumliches Phänomen handelt. Trotzdem führt jeder Oszillator eine Schwingung aus, daher können wir einige Begriffe aus der Schwingungslehre für Wellen weiter verwenden.
Amplitude \(A\) einer Welle: Ist die Amplitude ihrer Oszillatoren.
Frequenz \(f\) einer Welle: Ist die Frequenz ihrer Oszillatoren.
Periodendauer \(T\) einer Welle: Ist die Periodendauer ihrer Oszillatoren.
Die folgenden Begriffe sind jetzt neu und ergeben sich nur bei einer Welle:
Wellenberg (engl. crest): Jene Stellen einer Welle, bei denen die Auslenkung der Oszillatoren gerade der Amplitude entsprechen, heißen Wellenberge (Bild 9.8 (a)).
Wellental (engl. trough): Jene Stellen einer Welle, bei denen die Auslenkung der Oszillatoren gerade der negativen Amplitude entsprechen, heißen Wellentäler (Bild 9.8 (b)).
Ausbreitungsgeschwindigkeit \(c\) (engl. speed of propagation): Die Geschwindigkeit, mit der sich ein bestimmter Wellenberg (oder Wellental) entlang des Wellenmediums fortbewegt. Das ist nicht die Geschwindigkeit der Oszillatoren!
Wellenlänge \(\lambda\) (engl. wavelength): der Abstand zwischen zwei aufeinanderfolgender Wellenbergen. Alle Oszillatoren, die ein Vielfaches der Wellenlänge entfernt sind, schwingen gleichphasig (haben zum selben Zeitpunkt dieselbe Elongation).
Ausbreitungsrichtung (engl. direction of wave travel): Die Richtung, in die sich eine Welle fortbewegt (Blauer Pfeil in Bild 9.8).
harmonische Welle (engl. harmonic wave): Besteht ein Wellenmedium aus lauter harmonischen Oszillatoren, entsteht eine harmonische Welle. Das Foto einer harmonischen Welle ist eine Sinus- oder Kosinus-Kurve.
9.1.8 Vergleich Schwingungs- und Wellendiagramm
Das Schwingungs- und das Wellendiagramm einer harmonischen Welle sehen sehr ähnlich aus – beide zeigen eine Sinus- oder Kosinus-Kurve – und sind leicht zu verwechseln.
Im Diagramm 9.9 oben siehst du das Schwingungsdiagramm eines einzelnen Oszillators im Wellenmedium. Auf der waagrechten Achse ist die Zeit aufgetragen. Daher kannst du auch die Periodendauer der Schwingung in diesem Diagramm ablesen.
Das Diagramm 9.9 unten zeigt das Wellendiagramm (Foto einer Welle). Auf der waagrechten Achse ist wie die senkrechte Achse eine Ortsachse. In dem Diagramm kannst du die Lage aller Oszillator des Wellenmediums zu einem bestimmten Zeitpunkt sehen. Auf der senkrechten Achse erkennst du die Wellenamplitude \(A\), die identisch mit der Amplitude der Oszillatoren ist. Auf der waagrechten Achse kannst du die Wellenlänge \(\lambda\) erkennen.
Aus der Periodendauer \(T\) der Oszillatoren kannst du nicht auf die Wellenlänge \(\lambda\) der Welle schließen. Sie ist abhängig von den Kopplungskräften!
9.1.9 Wellenformen
Je nach Art der Anregung des Wellenmediums kannst du folgende Wellenformen unterscheiden (Bild 9.10):
- (kontinuierliche) Welle (engl. continuous wave): Entsteht bei einer ständigen Anregung.
- Wellenpaket (engl. wave train): Entsteht bei einer zeitlich begrenzten Anregung.
- Wellenpuls (engl. pulse): Entsteht bei einer sehr kurzen Anregung. Es entsteht ein einzelnes Wellental oder ein einzelner Wellenberg.
.jpg){kind=link}
