9.7 Reflexion und Brechung ebener Wellen
In Bild 9.53 siehst du die Wellen in einer Wellenwanne, bei der eine dreieckige Platte am Grund der Wellenwanne liegt.
Ändert sich das Ausbreitungsmedium bei Seilwellen, kommt es zur Reflexion und Transmission – daher die Welle teilt sich prinzipiell in zwei Anteile: einen zurückgeworfenen und einen fortlaufenden Teil. Außerdem wissen wir bereits, dass sich unterschiedliche Wellenmedien durch die unterschiedliche Ausbreitungsgeschwindigkeit einer Welle unterscheiden.
In diesem Kapitel werden wir die Reflexion und Transmission von ebenen Wellen untersuchen und mit dem Huygensschen Modell der Wellenausbreitung erklären.
9.7.1 Wellenwanne mit Untiefe
Im letzten Kapitel haben wir ebene Wellen anhand von Oberflächenwellen untersucht und zum Experimentieren eine Wellenwanne verwendet. Im Kapitel über Wasserwellen hast du erfahren, dass ihre Ausbreitungsgeschwindigkeit abhängig von der Wassertiefe ist – je größer die Wassertiefe, desto größer die Geschwindigkeit. Um das Verhalten von ebenen Wellen an der Grenze zwischen zwei Medien zu untersuchen, verwenden wir daher eine Wellenwanne, die aus zwei Bereichen mit unterschiedlicher Wassertiefe besteht (Bild 9.54).
Diese Anordnung werden wir in den folgenden Abschnitten verwenden.
9.7.2 Reflexion von Wellen
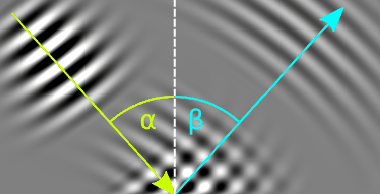
Am Ende eines Wellenmediums kommt es zur Reflexion von Wellen. In Bild 9.55 siehst du die Reflexion einer (annähernd) ebenen Wellenfront an einem Hindernis.
Die Wellenstrahlen der ein- und auslaufenden Wellenfront schließen denselben Winkel mit dem Einfallslot (kurz Lot) ein. Als Einfallslot wird eine Gerade bezeichnet, die im rechten Winkel auf die Grenze des Mediums steht (Normalvektor auf die Grenzfläche).
Das Reflexionsgesetz für Wellen lautet: \[\begin{equation} \alpha = \beta \tag{9.6} \end{equation}\] |
\(\alpha\) bezeichnet den Winkel zwischen einfallendem Wellenstrahl und Lot und \(\beta\) den Winkel zwischen ausfallendem Wellenstrahl und Lot.
9.7.3 Herleitung Reflexionsgesetz für Wellen
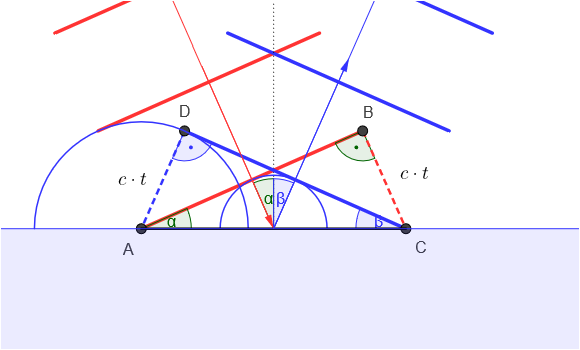
In Bild 9.56 siehst du die einfallenden ebenen Wellenfronten als rote Strecken. Ihr Wellenstrahl ist der rote Pfeil im rechten Winkel zu den Wellenfronten. Der Einfallswinkel ist \(\alpha\).
Trifft die Wellenfront \(\overline{AB}\) nach und nach auf die Grenzfläche, werden dort gemäß dem 1. Teil des Huygensschen Prinzips nach und nach kreisförmige Elementarwellen angeregt (blaue Kreise). Je früher sie angeregt wurden, desto weiter hat sie sich ausgebreitet und desto größer ist ihr aktueller Radius.
Nach dem 2. Teil des Huygensschen Prinzips ergibt sich die ausfallende Wellenfront \(\overline{DC}\) (blaue Strecken) als Einhüllende der blauen Kreise.
Wir vergleichen jetzt die zwei rechtwinkeligen Dreiecke \(\triangle ABC\) (rot) und \(\triangle ACD\) (blau). Beide Dreiecke haben als Hypotenuse dieselbe Strecke \(\overline{AC}\). Da sich sowohl die roten Wellenfronten als auch die blauen Elementarwellen im selben Medium befinden, breiten sich beide mit der Geschwindigkeit \(c\) aus. Daher benötigt die Wellenfront von \(B\) nach \(C\) dieselbe Zeit wie die Elementarwelle von \(A\) nach \(D\). Damit sind die zurückgelegten Strecken \(c\cdot t\) und \(\overline{AD} = \overline{CB}\) gleich lang.
Zwei rechtwinkelige Dreiecke, die zwei gleich lange Seiten haben, sind kongruent (Deckungsgleich). Damit sind auch die Winkel \(\alpha\) und \(\beta\) in den Dreiecken gleich groß. Diese Winkel entsprechen dem Einfallswinkel \(\alpha\) und dem Ausfallswinkel \(\beta\) der Wellenstrahlen. Damit ist das Reflexionsgesetz gezeigt.
9.7.4 Brechung von Wellen
Die Ausbreitungsgeschwindigkeit von Wasserwellen hängt von der Wassertiefe ab. Legen wir eine Platte in die Wellenwanne, ist dort das Wasser seichter und die Wasserwellen können sich in diesem Bereich nur langsamer ausbreiten.
In Bild 9.57 siehst du eine ebene Welle auf die Grenzfläche zweier unterschiedlich tiefer Bereiche zulaufen. Ändern sich die Eigenschaften des Wellenmediums, wird ein Teil der Welle reflektiert und der restliche Teil der Welle breitet sich im neuen Medium aus. Da die Frequenz einer Welle unverändert bleibt, sich aber die Ausbreitungsgeschwindigkeit ändert, muss sich nach der Grundgleichung der Wellenlehre die Wellenlänge im neuen Medium ändern.
Eine Änderung der Wellengeschwindigkeit bewirkt auch eine Änderung der Ausbreitungsrichtung. Kommt es beim Übergang in ein zweites Medium zu einer Verlangsamung der Wellengeschwindigkeit, wird der Brechungswinkel \(\beta\) zwischen Wellenstrahl und Lot kleiner als der Einfallwinkel \(\alpha\). Das wird als „Brechung zum Lot“ bezeichnet. Kommt es hingegen beim Übergang in ein zweites Medium zu einer Vergrößerung der Wellengeschwindigkeit, vergrößert sich der Brechungswinkel \(\beta\). In diesem Fall wird von einer „Brechung vom Lot“ gesprochen.
Zwischen den Ausbreitungsgeschwindigkeiten in beiden Medien \(c_1\) und \(c_2\), dem Einfallswinkel \(\alpha\) und dem Brechungswinkel \(\beta\) gibt es einen Zusammenhang.
Das Brechungsgesetz für Wellen lautet: \[\begin{equation} \frac{\sin(\alpha)}{\sin(\beta)} = \frac{c_1}{c_2} \tag{9.7} \end{equation}\] |
9.7.5 Herleitung Brechungsgesetz für Wellen
Wie du in Bild 9.57 gesehen hast, kommt es an der Grenzfläche zwischen zwei Medien immer zu einer reflektierten und einer gebrochenen Welle. Da die Reflexion von Wellen schon in der Herleitung des Reflexionsgesetzes erklärt wurde, wird im Rest des Abschnitts nur die gebrochene Welle gezeigt.
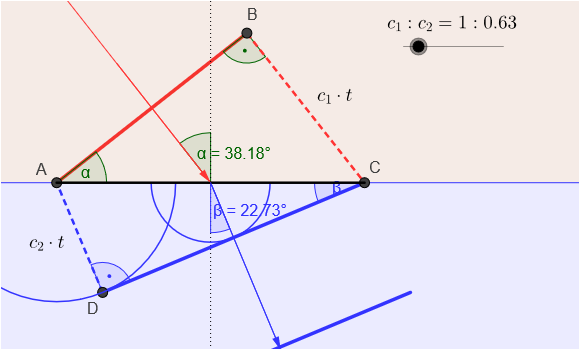
In Bild 9.58 siehst du die einfallenden ebenen Wellenfronten als rote Strecken. Ihr Wellenstrahl ist der rote Pfeil im rechten Winkel zu den Wellenfronten. Der Einfallswinkel ist \(\alpha\).
Trifft die Wellenfront \(\overline{AB}\) nach und nach auf die Grenzfläche, werden dort gemäß dem 1. Teil des Huygensschen Prinzips nach und nach kreisförmige Elementarwellen angeregt (blaue Kreise), die sich auch im zweiten Medium ausbreiten. Je früher sie angeregt wurden, desto weiter haben sie sich ausgebreitet und desto größer ist ihr aktueller Radius.
Nach dem 2. Teil des Huygensschen Prinzips ergibt sich die gebrochene Wellenfront \(\overline{DC}\) (blaue Strecken) als Einhüllende der blauen Kreise im zweiten Medium.
Wir vergleichen jetzt die zwei rechtwinkeligen Dreiecke \(\triangle ABC\) (rot) und \(\triangle ACD\) (blau). Beide Dreiecke haben als Hypotenuse dieselbe Strecke \(\overline{AC}\).
Die roten Wellenfronten (Medium 1) breiten sich mit der Geschwindigkeit \(c_1\) aus, während die blauen Elementarwellen (Medium 2) sich mit der Geschwindigkeit \(c_2\) ausbreiten. In der Zeit \(t\), in der sich der Punkt \(B\) der roten Wellenfront bis zum Punkt \(C\) ausgebreitet hat (also den Weg \(c_1\cdot t\) zurückgelegt hat), ist die im Punkt \(A\) angeregte Elementarwelle bis auf einen Radius von \(c_2\cdot t\) (die Länge der Strecke \(\overline{AD}\)) angewachsen.
Für das rote Dreieck \(\triangle ABC\) gilt:
\[ \sin(\alpha) = \frac{\text{Gegenkathete}}{\text{Hypotenuse}} = \frac{|\overline{BC}|}{|\overline{AC}|} = \frac{c_1\cdot t}{|\overline{AC}|} \]
und
\[ \begin{aligned} \sin(\alpha) = {} & \frac{c_1\cdot t}{|\overline{AC}|} \qquad\Bigr\rvert\cdot\frac{|\overline{AC}|}{\sin(\alpha)} \\ |\overline{AC}| = {} & \frac{c_1\cdot t}{\sin(\alpha)} \\ \end{aligned} \]
Dieselben Schritte führen wir für das blaue Dreieck \(\triangle ACD\) durch und erhalten:
\[ |\overline{AC}| = \frac{c_2\cdot t}{\sin(\beta)} \]
Wir setzen die Längen \(|\overline{AC}|\) der Hypotenusen gleich und erhalten:
\[ \begin{aligned} \frac{c_2\cdot t}{\sin(\beta)} = {} & \frac{c_1\cdot t}{\sin(\alpha)} &&\Bigr\rvert\cdot \frac{1}{t} \\ \frac{c_2}{\sin(\beta)} = {} & \frac{c_1}{\sin(\alpha)} &&\Bigr\rvert\cdot \frac{\sin(\alpha)}{c_2} \\ \frac{\sin(\alpha)}{\sin(\beta)} = {} & \frac{c_1}{c_2} \\ \end{aligned} \]
Der Winkel \(\alpha\) im roten Dreieck entspricht dem Einfallswinkel der roten Wellenfronten und der Winkel \(\beta\) im blauen Dreieck dem Brechungswinkel der blauen Wellenfronten. Damit ist das Brechungsgesetz gezeigt.
9.7.6 Totalreflexion von Wellen
Das Reflexions- und Brechungsgesetz gelten, egal aus welcher Richtung die Welle an die Grenze zwischen zwei Wellenmedien stößt. Kommt die Welle allerdings aus dem Wellenmedium mit der kleineren Ausbreitungsgeschwindigkeit, kann es einen Sonderfall geben. Laufen die Wellen sehr flach gegen die Grenzfläche, kommt es zu der sogenannten Totalreflexion (engl. total internal reflection) (Bild 9.59).
In diesem Fall überlagern sich die Wellen unmittelbar hinter der Grenzschicht destruktiv, sodass die Wellen nach einem Abstand von ein paar Wellenlängen dort vollständig ausgelöscht werden. Die gesamte Wellenenergie verbleibt in der reflektierten Welle. Der Einfallswinkel, ab dem es zur Totalreflexion kommt, wird Grenzwinkel der Totalreflexion genannt.
9.7.7 Verhinderte Totalreflexion
Wie du im letzten Abschnitt gesehen hast, dringt selbst bei der Totalreflexion die Welle ein paar Wellenlängen weit in das Medium mit der größeren Wellenausbreitungsgeschwindigkeit ein. Diese exponentiell abklingende Welle kann zum Beispiel in der Optik für einen Strahlenteiler gezielt ausgenutzt werden (Bild 9.60).
Befindet sich knapp hinter der totalreflektierenden Grenzfläche ein drittes Wellenmedium mit kleinerer Wellenausbreitungsgeschwindigkeit, können sich dort nicht mehr alle Elementarwellen auslöschen und ein Teil der Welle läuft im dritten Medium weiter. Dieser Effekt wird verhinderte Totalreflexion (engl. frustrated total internal reflection) genannt. Sind das erste und das dritte Medium gleich, lässt sich die Größe des Anteils der „abgezweigten“ Welle durch die Größe der Spaltbreite exakt regeln. Wird die Spaltbreite schließlich null, gibt es gar keinen Spalt mehr und \(100\,\%\) der Wellen laufen weiter – in diesem Fall gibt es gar keine reflektierten Anteil mehr.
9.7.8 Seismische Wellen
Die bisher tiefste geologische Bohrung (Kola-Bohrung) kommt gerade einmal auf eine Tiefe von rund \(12\;\mathrm{km}\). Das ist lediglich ein Promille des Erdradius. Woher kennen wir dann den Aufbau der Erde so genau (Bild 9.61)?
Bei einem schweren Erdbeben entstehen neben den 2-dimensionalen Oberflächenwellen auch 3-dimensionale Transversal- und Longitudinalwellen, die sich durch die gesamte Erde fortpflanzen. Diese seismischen Wellen (engl. seismic waves) werden von einem weltweiten Netzwerk von Seismografen aufgezeichnet. Die Laufzeiten der einzelnen Wellen und deren Reflexionen an unterirdischen Grenzschichten lassen Rückschlüsse auf den Aufbau der Erde zu.
Ändert sich die Dichte der Erde zum Beispiel an einer Stelle sprunghaft, kommt es zur teilweisen Reflexion (Bild 9.62). Da wir außerdem wissen, dass sich Transversalwellen nur in Festkörpern ausbreiten können und sich diese nicht durch den äußeren Kern ausbreiten, wissen wir sogar, dass dieser flüssig ist.