9.6 Ebene Wellen
Sicher hast du schon einmal mit Wellen in einer Badewanne oder in einem Schwimmbecken experimentiert (Bild 9.45)…
Bisher haben wir uns mit 1-dimensionalen Wellen beschäftigt. In diesem Kapitel geht es um ebene Wellen. Zur Untersuchung der ebenen Wellen verwenden wir Oberflächenwellen in einer Wellenwanne (engl. ripple tank). Die mit der Wellenwanne gewonnenen Erkenntnisse führten Ende des 17. Jahrhunderts zur Formulierung des Huygensschen Prinzips (engl. Huygens’ principle) der Wellenausbreitung (benannt nach Christiaan Huygens Audio abspielen , gesprochen wie „Hörens“). Auch wenn Wasserwellen zum Experimentieren verwendet wurden: Die Ergebnisse in diesem Kapitel gelten für alle Arten von ebenen und räumlichen Wellen.
Links:
- App: Wellen Interferenz
9.6.1 Grundbegriffe für ebene (und räumliche) Wellen
In Bild 9.46 siehst du links einen punktförmigen Wellenerreger und auf der rechten Seite einen stabförmigen Wellenerreger. Die zusammenhängenden hellen und dunklen Streifen werden als Wellenfronten (engl. wavefront) bezeichnet. Alle Teile einer Wellenfront sind zur selben Zeit von dem Wellenerreger angeregt worden. Die Helligkeit eines Streifens verrät dir die Phase einer Wellenfront. Bei allen dunklen Stellen befinden sich die Oszillatoren des Mediums zum Beispiel gerade am Maximum (Amplitude) ihrer Bewegung, bei allen hellen Stellen gerade am Minimum (negative Amplitude).
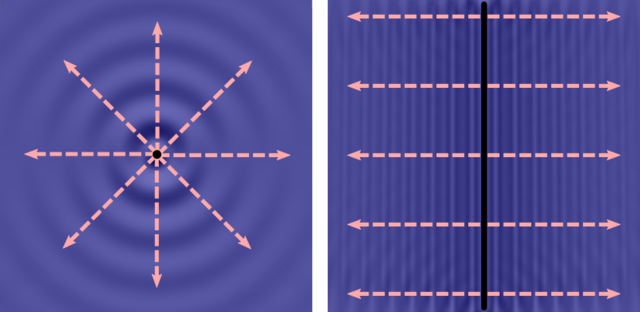
Bild 9.46: Wellenfronten und -strahlen bei einem kreisförmigen (links) und einem stabförmigen Erreger (rechts)
Die im Bild 9.46 eingezeichneten Pfeile, werden Wellenstrahlen (engl. rays) genannt. Sie zeigen die Richtung der Ausbreitung einer Wellenfront an und stehen immer im rechten Winkel zu den Wellenfronten.
9.6.2 Huygenssches Prinzip – 1. Teil
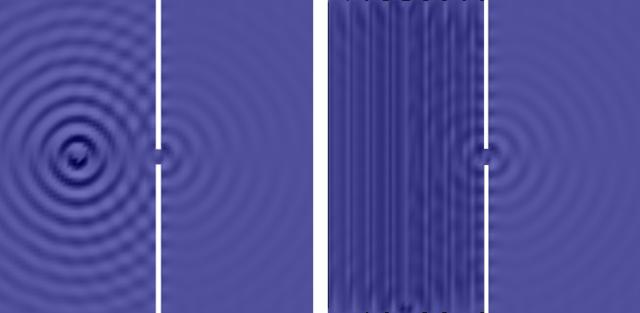
Wenn wir den kleinsten Teil einer Wellenfront, eine sogenannte Elementarwelle (engl. wavelet), erhalten wollen, erscheint es sinnvoll, sie durch einen Spalt laufen zu lassen und diesen Spalt immer weiter zu verkleinern (Bild 9.47).
Unabhängig von der ursprünglichen Form der Wellenfront hat die Elementarwelle immer die Form einer (punktförmig erregt gedachten) Kreiswelle.
| Jeder Punkt einer Wellenfront kann als Ausgangspunkt einer Elementarwelle aufgefasst werden. (Huygenssche Prinzip, 1. Teil) |
9.6.3 Huygenssches Prinzip – 2. Teil
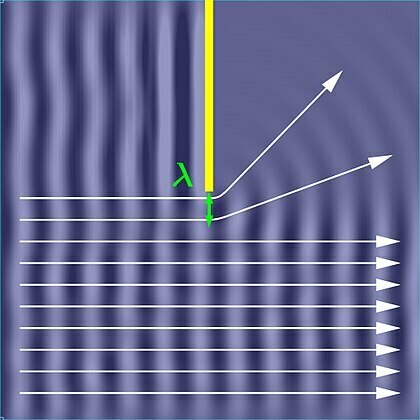
Simulieren wir Elementarwellen durch eine Reihe punktförmiger Erreger (Bild 9.48), kannst du erkennen, dass wir damit eine ebene Welle (links) oder eine Kreiswelle (rechts) erzeugen können.
Die Einhüllende (engl. envelope) von einer Wellenfront erzeugten Elementarwellen, liefert eine neue Wellenfront.
| Jede neue Wellenfront kann als Einhüllende von Elementarwellen einer Wellenfront verstanden werden. (Huygenssche Prinzip, 2. Teil) |
Die zwei Teile des Huygensschen Prinzips können verwendet werden, um Wellenphänomene wie Beugung, Brechung und Reflexion zu verstehen.
9.6.4 Beugung
Mit Beugung (engl. diffraction) wird die Ablenkung von Wellen an einem Hindernis oder an einer Öffnung bezeichnet (Bild 9.49). Im Gegensatz zu Teilchen (etwa einem Tennisball) können Wellen in den geometrischen Schattenraum (11.2.1; Bereich hinter einem Hindernis) vordringen.
Da nach dem Huygensschen Prinzip (1. Teil) jeder Punkt einer Wellenfront Ausgangspunkt einer Elementarwelle ist, entstehen am Rand der Wellenfront Kreiswellen, die sich in den Schattenraum ausbreiten und überlagern.
Sind Öffnung/Hindernis von der Größenordnung der Wellenlänge, kommt es zu deutlichen Beugungserscheinungen. Sind Öffnung/Hindernis dagegen viel größer als die Wellenlänge, sind die Amplituden der gebeugten Wellen im Schattenraum vernachlässigbar klein. Aus diesem Grund kannst du auch ohne Hilfsmittel „um die Ecke“ hören (Schallwellenlänge im Meter-Bereich), aber nicht „um die Ecke“ sehen (Lichtwellenlänge im Nanometer-Bereich).
Links:
- WebApp: Virtuelle Wellenwanne
9.6.5 Interferenz zweier Kreiswellen
Wir erzeugen durch periodisches Eintauchen einer zweizinkigen Gabel zwei Kreiswellen mit gleicher Wellenlänge auf einer Wasseroberfläche. Die Wellenfronten beider Quellen überlagern sich und bilden das Interferenzmuster (engl. interference pattern) in Bild 9.50.
In Bild 9.51 kannst du sehen, wie dieses Muster zustande kommt. Die Linien zeigen die Wellenfronten des blauen und roten Erregers in einer Momentaufnahme. Durchgezogene Linien zeigen Wellenberge, gepunktete Linien zeigen Wellentäler. Treffen an einer Stelle einander zwei Wellenberge oder zwei Wellentäler, verstärken sich dort die Amplituden zu allen Zeiten und wir erhalten konstruktive Interferenz (weiße Punkte). Trifft an einer Stelle allerdings ein Wellental auf einen Wellenberg, schwächen sich dort die Amplituden zu allen Zeiten und wir erhalten destruktive Interferenz (schwarze Punkte).

Bild 9.51: Interferenzmusters bei zwei punktförmigen Wellenerregern. Weiße Punkte markieren Stellen konstruktiver Interferenz, schwarze Punkte Stellen mit destruktiver Interferenz
Diese Stellen maximaler Verstärkung und Auslöschung breiten sich entlang von Hyperbeln aus (schwarze Linien in Bild 9.51).
9.6.6 Aus eins mach zwei
Das Interferenzmuster zweier punktförmiger Erreger lässt sich auch auf eine andere Art und Weise erzeugen. Dazu platzieren wir eine Blende mit einem Doppelspalt (Hindernis mit zwei Öffnungen) nach einem einzigen Wellenerreger. Sobald die Wellenfronten die Blende erreichen, erregen diese in den Öffnungen je eine kreisförmige Elementarwelle (Huygenssches Prinzip – 1. Teil). Sind die beiden Öffnungen auch noch gleich weit von einer punktförmigen Quelle entfernt, regt dieselbe Wellenfront beide Elementarwellen in den Spaltöffnungen an. Damit sind die Elementarwellen sogar gleichphasig und wir erhalten das identische Interferenzmuster (Bild 9.52, b).

Bild 9.52: Interferenzmuster durch (a) zwei Erreger und (b) einem Erreger und einer Doppelspalt-Blende
Da der größte Teil der Welle durch das Hindernis ausgeblendet wird, ist das hinter der Blende entstehende Interferenzmuster wesentlich schwächer als bei zwei punktförmigen Erregern.