13.14 Maxwell Gleichungen
Vielleicht hast du schon einmal das T-Shirt in Bild 13.177 gesehen und dich gewundert, was diese Gleichungen bedeuten.
Es handelt sich um die sogenannten Maxwell-Gleichungen (engl. Maxwell’s equations). Sie können nicht hergeleitet werden, sondern sind der Höhepunkt jahrzehntelanger Forschung. Sie fassen unser gesamtes Wissen über den Elektromagnetismus in nur vier kurzen Gleichungen zusammen. Ein Physik-Professor soll einmal in einer Vorlesung gesagt haben:
„Dies sind die Maxwell-Gleichungen. Nur vier kompakte Gleichungen. Mit ein wenig Arbeit ist es leicht, die Grundelemente der Gleichungen zu verstehen - was all die Symbole bedeuten, wie wir alle relevanten Größen berechnen können, und so weiter. Aber während es einfach ist, die Elemente der Gleichungen zu verstehen, ist es eine andere Sache, alle ihre Konsequenzen zu verstehen. In diesen Gleichungen ist der gesamte Elektromagnetismus enthalten - alles von Antennen über Motoren bis hin zu Schaltkreisen. Wenn Sie glauben, die Konsequenzen dieser vier Gleichungen zu verstehen, dann dürfen Sie jetzt den Raum verlassen und können am Ende des Semesters wiederkommen und die Prüfung mit einer Eins abschließen.“
In diesem Kapitel versuchen wir dir möglichst anschaulich zu erklären, was jede dieser Gleichungen bedeutet.
13.14.1 Übersicht Maxwell Gleichungen
Die vier Maxwell-Gleichungen beschreiben das elektrische Feld \(E\) und das magnetische Feld \(B\) und werden daher auch als Feldgleichungen bezeichnet. Sie wurden von James Clerk Maxwell aufgestellt und 1864 vervollständigt. So wie die drei Newton Axiome die gesamte Mechanik beschreiben, beschreiben die folgenden vier Gleichungen (zusammen mit der Lorentzkraft) alle elektrischen und magnetischen Phänomene im Vakuum (und damit auch annähernd in Luft) – das ist schon sehr bemerkenswert.
\[\begin{align} \oint \vec{E}\cdot d\vec{A} = {} & \frac{Q}{\varepsilon_0} \notag \\ \oint \vec{B}\cdot d\vec{A} = {} & 0 \notag \\ \oint \vec{E}\cdot d\vec{s} = {} & -\frac{d\Phi_B}{dt} \notag \\ \oint \vec{B}\cdot d\vec{s} = {} & \mu_0\cdot I+\mu_0\cdot\varepsilon_0\cdot \frac{d\Phi_E}{dt} \notag \\ \end{align}\]
Konkret lassen sich mit diesen Gleichungen aus bekannter Ladungs- oder Stromverteilung die Größe von elektrischen und magnetischen Feldern berechnen. Auch wenn du vermutlich einige mathematische Symbole in den Formeln nicht kennst und nichts damit anzufangen weißt: Mach dir nichts daraus. In den folgenden Kapiteln werden wir jede Formel einzeln besprechen und die Ideen dahinter erklären. Die meisten davon sind dir schon in früheren Kapiteln begegnet – auch wenn sie hier etwas anders aussehen.
Was dir aber sofort auffallen sollte, ist eine gewisse Symmetrie in der Struktur der Gleichungen: Die erste und zweite Formel sowie die dritte und vierte sind von ihrem Aufbau immer sehr ähnlich. In der ersten und dritten Formel geht es um das elektrische Feld \(E\) und in den Gleichungen zwei und vier um das magnetische Feld \(B\). Das elektrische und das magnetische Feld sind in den Gleichungen fast gleichberechtigt.
Und ja, es gibt auch vier Gleichungen, die den Elektromagnetismus in Materie vollständig beschreiben und die elektrische Polarisation und die Magnetisierung von Stoffen berücksichtigen. Diese Gleichungen sind noch etwas komplizierter und benötigen wir hier nicht.
Von den Maxwell-Gleichungen gibt es auch noch andere gleichwertige mathematische Formulierungen. Also wundere dich nicht, wenn du auf anderen T-Shirts zum Beispiel ein \(\nabla\)-Symbol entdeckst – der Inhalt der Formeln ist immer gleich.
Streng genommen reichen diese vier Gleichungen für eine vollständige Beschreibung des Elektromagnetismus nicht aus. Die Maxwell-Gleichungen beschreiben zwar den Zusammenhang von elektrischen und magnetischen Feldern und ihre Wechselwirkung mit elektrischen Ladungen und Strömen. Sie beschreiben aber nicht, wie sich diese Felder auf die Bewegung von Ladungsträgern auswirken. Dafür benötigen wir noch zusätzlich das elektromagnetische Kraftgesetz.
13.14.2 Bedeutung der mathematischen Symbole
Das langgezogene stilisierte „S“ steht in der Mathematik für das Integral. Dabei handelt es sich um eine Summe von sehr vielen, sehr kleinen Summanden (Genaueres erfährst du im mathematischen Zweig der Differenzialrechnung).
Betrachten wir zunächst diese Form:
\[\begin{equation} \oint (\ldots) \cdot d\vec{s} \tag{13.32} \end{equation}\]
In der Physik verwenden wir das kleine \(s\) für einen Weg oder Strecke. Der gesamte Ausdruck entspricht einer Summe entlang eines geschlossenen Weges, wenn wir ihn in sehr kleinen Wegabschnitten entlanggehen. Dass es sich immer um einen „geschlossenen“ Weg handeln muss, erkennst du an dem Kreis im Integralzeichen. Was genau entlang des Weges summiert wird, ergibt sich aus dem jeweiligen Ausdruck in der Klammer.
Wichtig ist, dass nicht vorgeschrieben ist, welcher konkrete Weg genommen wird. Die Gleichung gilt für jeden beliebigen geschlossenen Weg, und sei er noch so exotisch (Bild 13.178).
Sehr ähnlich ist die Form:
\[\begin{equation} \oint (\ldots) \cdot d\vec{A} \tag{13.33} \end{equation}\]
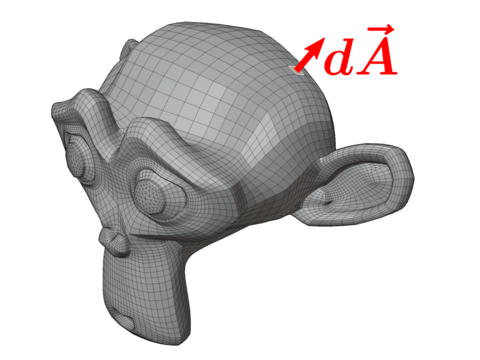
Üblicherweise steht das Formelsymbol \(A\) in der Mathematik und Physik für eine Fläche. Der gesamte Ausdruck entspricht dieses Mal der Summe über eine geschlossene Oberfläche, wenn wir sehr kleine Flächenelemente nehmen. Dass es sich immer um eine „geschlossene“ Oberfläche handeln muss, erkennst du wieder am Kreis im Integralzeichen. Was genau über die Oberfläche summiert wird, ergibt sich wieder aus dem jeweiligen Klammerausdruck.
Auch hier ist nicht vorgeschrieben, welche konkrete Oberfläche genommen wird. Die Gleichung gilt für jede beliebige geschlossene Oberfläche, und sei sie noch so exotisch (Bild 13.179).
13.14.3 Gleichung 1 - Das Gaußsche Gesetz
Die Gleichung
\[\begin{equation} \oint \vec{E}\cdot d\vec{A} = \frac{Q}{\varepsilon_0} \tag{13.34} \end{equation}\]
wird als Gaußsches Gesetz (engl. Gauss’s law) bezeichnet. Im Integral siehst du das Produkt aus elektrischer Feldstärke und einem sehr, sehr kleinen Flächenelement. Es wird als elektrischer Fluss bezeichnet und entspricht anschaulich der Anzahl der Feldlinien durch das Flächenelement. Bei dem Integral (Summe) geht es also um den Gesamtfluss durch eine geschlossene Oberfläche (Bild 13.180).
In einem früheren Abschnitt haben wir bereits gezeigt, dass bei einer Kugeloberfläche um eine Punktladung der gesamte elektrische Fluss proportional zur eingeschlossenen Ladung ist. Die Maxwell-Gleichung ist eine Verallgemeinerung und besagt, dass dies für jede geschlossene Oberfläche gilt. Die Kernaussage ist:
| Elektrische Ladungen erzeugen ein elektrostatisches Feld. |
13.14.4 Coulombsche und Gaußsche Gesetz
Im Gaußschen Gesetz ist das Coulombsche Kraftgesetz enthalten. Um das zu erkennen, sieh dir das Bild 13.181 an.
Das Gaußsche Gesetz besagt, dass der Gesamtfluss durch jede Oberfläche, die eine Ladung vollständig umschließt, gleich groß ist. Wir können daher auch eine Kugelschale wählen. Da die Formel für die Oberfläche einer Kugel \(A=4\pi\cdot r^{2}\) lautet, ist die Oberfläche für eine Kugelschale mit doppelten Radius dann 4-Mal so groß. Damit der Fluss durch beide Kugelschalen gleich groß bleibt, muss die elektrische Feldstärke in doppelter Entfernung auf \(1/4\) gesunken sein. Da die Coulomb-Kraft proportional zur elektrischen Feldstärke ist, folgt daraus die \(1/r^2\)-Abhängigkeit der elektrischen Kraft.
13.14.5 Gleichung 2 - Das Gaußsche Gesetz für Magnetfelder
Die Gleichung
\[\begin{equation} \oint \vec{B}\cdot d\vec{A} = 0 \tag{13.35} \end{equation}\]
wird als Gaußsches Gesetz für Magnetfelder (engl. Gauss’s law for magnetism) bezeichnet.
Wie im Gaußschen Gesetz geht es bei diesem Integral (Summe) um den Gesamtfluss durch eine geschlossene Oberfläche. Aber in dieser Gleichung geht es um den magnetischen Fluss.
Betrachte beispielsweise das Feld eines Ringmagneten in Bild 13.182. Die Feldlinien in einem Magnetfeld sind immer geschlossen (Wirbelfeld). Jede Feldlinie, die durch die geschlossene Oberfläche eintritt, kommt an einer anderen Stelle wieder aus ihr heraus. Das Ergebnis ist unabhängig von der Form der Oberfläche.
Das Gaußsche Gesetz für Magnetfelder besagt jetzt genau das: In einem Magnetfeld gilt für alle geschlossenen Oberflächen, dass der magnetische Gesamtfluss („hinein“ minus „heraus“) zu allen Zeiten null ist. Die Kernaussage ist:
| Es gibt keine magnetischen Ladungen (magnetische Monopole). |
Das Fehlen von magnetischen Ladungen ist der Grund dafür, dass die Gleichungen bezüglich des elektrischen und magnetischen Feldes nicht vollkommen symmetrisch sind.
13.14.6 Gleichung 3 - Das Induktionsgesetz
Die Gleichung
\[\begin{equation} \oint \vec{E}\cdot d\vec{s} = -\frac{d\Phi_B}{dt} \tag{13.36} \end{equation}\]
wird als Induktionsgesetz (engl. Faraday’s law) bezeichnet. Wie der Name schon sagt, handelt es sich um eine andere Formulierung des Faradayschen Induktionsgesetzes. Auf der rechten Seite steht die zeitliche Änderung des magnetischen Flusses und das Minus drückt die Lenzsche Regel aus.
Aber was bedeutet die linke Seite? Die elektrische Feldstärke \(E\) entspricht der Kraft auf eine Einheitsladung. Der Ausdruck „Kraft mal Weg“ entspricht allgemein einer physikalischen Arbeit. Die linke Seite entspricht daher der Gesamtverschiebearbeit einer Einheitsladung entlang eines beliebigen geschlossenen Weges in einem elektrischen Feld.
In einem elektrostatischen Feld ist die Verschiebearbeit für einen geschlossenen Weg immer null. Ist die Verschiebearbeit entlang eines beliebigen geschlossenen Weges durch ein elektrisches Feld jedoch ungleich null, muss sie von einem induzierten elektrischen Wirbelfeld stammen. Die dritte Maxwell-Gleichung besagt jetzt: Die gesamte Verschiebearbeit in einem elektrischen Feld ist der zeitlichen magnetischen Flussänderung proportional. Die Kernaussage ist:
| Ein zeitlich veränderliches Magnetfeld führt zu einem elektrischen Wirbelfeld. |
13.14.7 Gleichung 4 - Das erweiterte Durchflutungsgesetz
Die Gleichung
\[\begin{equation} \oint \vec{B}\cdot d\vec{s} = \mu_0\cdot I+\mu_0\cdot\varepsilon_0\cdot \frac{d\Phi_E}{dt} \tag{13.37} \end{equation}\]
wird als erweitertes Durchflutungsgesetz (engl. Ampère’s law with Maxwell’s addition) bezeichnet.
Nachdem das Gaußsche Gesetz für Magnetfelder die Existenz von „magnetischen Ladungen“ ausschließt, geht es in der 4. Maxwell-Gleichung um die Ursachen eines Magnetfeldes.
Die rechte Seite besteht aus zwei Summanden. Der erste Summand besagt, dass ein elektrischer Strom ein Magnetfeld verursacht. Der zweite Summand – das ist die Erweiterung durch Maxwell – besagt, dass auch eine zeitliche elektrische Flussänderung ein Magnetfeld hervorruft. Die Größe des Magnetfeldes ist dabei der Stromstärke und der zeitlichen elektrischen Flussänderung proportional. Die Kernaussage ist:
| Ein Magnetfeld entsteht entweder durch einen elektrischen Strom und/oder ein zeitlich veränderliches elektrisches Feld. |
13.14.8 Maxwell Gleichungen und Licht
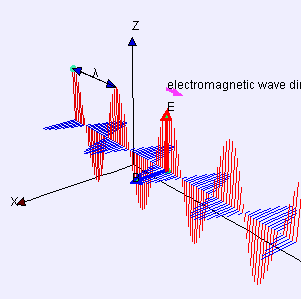
Die dritte und vierte Maxwell Gleichung besagen sinngemäß, dass ein zeitlich veränderliches magnetisches Feld ein elektrisches Feld erzeugt und dass umgekehrt ein zeitlich veränderliches elektrisches Feld ein magnetisches Feld erzeugt. Das beschreibt die Ausbreitung einer elektromagnetischen Welle, wie sie in Bild 13.183 dargestellt ist. Dabei stehen der Vektor des elektrischen Feldes (rot) und der Vektor des magnetischen Feldes (blau) jeweils im rechten Winkel zur Ausbreitungsrichtung der Welle.
Licht selbst ist aber nichts anderes als eine elektromagnetische Welle einer bestimmten Wellenlänge, die für unsere Augen sichtbar ist.
In der vierten Gleichung steckt außerdem der Faktor \(\mu_0\cdot\varepsilon_0\). Für das Produkt aus elektrischer Feldkonstante \(\varepsilon_0\) und magnetischer Feldkonstante \(\mu_0\) gilt:
\[ \mu_0\cdot\varepsilon_0 = \frac{1}{c^2} \]
Wobei \(c\) die Lichtgeschwindigkeit bedeutet. Das ist kein Zufall, denn jede elektromagnetische Welle – nicht nur Licht – breitet sich mit dieser Geschwindigkeit im Vakuum aus.
In den Newtonschen Gleichungen der Mechanik kommen nur Beschleunigungen vor. Damit gelten die Gleichungen universell für jedes unbeschleunigte Bezugssystem (Inertialsystem). Dass in den Maxwell-Gleichungen eine absolute Geschwindigkeit (die Lichtgeschwindigkeit) vorkommt, war Ende des 19. Jahrhunderts ein großes Problem. Auch die Maxwell-Gleichungen sollten für jedes Inertialsystem gelten. Geschwindigkeiten – anders als Beschleunigungen – sind in zueinander bewegten Inertialsystemen unterschiedlich groß. Diesen Widerspruch konnte erst Albert Einstein viele Jahre später durch die Relativitätstheorie auflösen. Seine erste Arbeit dazu trägt daher den Namen „Zur Elektrodynamik bewegter Körper“ – obwohl die Erkenntnisse der Relativitätstheorie alle Bereiche der Physik betreffen.
13.14.9 Feldgleichung für die Gravitation
Vielleicht hast du dich gefragt, ob es – analog zu den Maxwell-Gleichungen im Elektromagnetismus – auch für das Gravitationsfeld ein System aus Feldgleichungen gibt, die statt des Newtonschen Gravitationsgesetzes verwendet werden können. Die Antwort ist ja. Und da es nur eine Art von Masse gibt und Gravitationskräfte immer anziehend sind, lässt sich das Gravitationsfeld sogar nur durch eine einzige Feldgleichung beschreiben. Die Struktur der Feldgleichung gleicht dem Gaußschen Gesetz für Ladungen. Die Feldgleichung für das Gravitationsfeld (engl. Gauss’s law for gravity) lautet:
\[\begin{equation} \oint \vec{g}\cdot d\vec{A} = -4\pi\cdot G\cdot M \tag{13.38} \end{equation}\]
Bei dem Integral (Summe) geht es um den Gesamtfluss durch eine geschlossene Oberfläche. An die Stelle der elektrischen Feldstärke \(\vec{E}\) tritt die Gravitationsfeldstärke \(\vec{g}\). Für jede beliebige geschlossene Oberfläche ist der (Gravitations-)Fluss proportional zur eingeschlossenen Masse \(M\).
Das Newtonsche Kraftgesetz lässt sich aus dieser Feldgleichung auf dieselbe Weise herleiten wie das Coulombsche Kraftgesetz aus dem Gaußschen Gesetz für elektrische Ladungen.
