17.3 Doppelspalt-Experimente
In den letzten Kapiteln hast du gesehen, dass sich Lichtwellen im Mikrokosmos wie Teilchen verhalten können und auch Elektronen wie Wellen. Das wird auch als Welle-Teilchen-Dualismus (engl. wave-particle duality) bezeichnet.
In diesem Kapitel werden wir uns ausführlich mit dem Doppelspalt-Experiment beschäftigen. Wir werden für verschiedene Quellen untersuchen, was auf dem Schirm hinter dem Doppelspalt zu beobachten ist. Außerdem werden wir versuchen zu ergründen, warum sich sehr kleine Objekte anders verhalten, als wir es von großen Objekten gewohnt sind. Dabei werden wir ähnliche rätselhafte Situationen erleben wie in Bild 17.24.
Links:
- Video: Wave Particle Duality
17.3.1 Doppelspalt-Experimente mit klassischen Teilchen
Zunächst führen wir den Doppelspalt-Versuch mit klassischen Teilchen – zum Beispiel mit Tennisbällen – durch (Bild 17.25). Dazu benötigen wir eine Ballwurfmaschine (1), die Tennisbälle auf eine Mauer mit zwei Spaltöffnungen (2) schießt. Hinter der Mauer befindet sich der Detektor mit einer Reihe von Bechern, die alle Bälle hinter dem Schirm auffangen (3). Hinter jedem der Spalte befindet sich zusätzlich je eine automatische Sprühanlage mit unterschiedlicher Farbe. Kommt ein Ball durch den Spalt, wird er mit der jeweiligen Spalt-Farbe markiert.
Beginnen wir das Experiment, in dem wir den unteren Spalt schließen. Alle am Detektor eintreffenden Bälle müssen logischerweise durch den oberen Spalt gekommen sein. Entlang des Detektors erhältst du eine Verteilung \(P_1\) (Bild 17.25a).
Als Nächstes schließen wir den oberen Spalt. Alle am Detektor eintreffenden Bälle müssen jetzt durch den unteren Spalt gekommen sein. Entlang des Detektors erhältst du eine Verteilung \(P_2\). Da wir eine zum ersten Experiment symmetrische Versuchsanordnung haben, ist es nicht verwunderlich, dass die Verteilungen \(P_1\) und \(P_2\) spiegelbildlich gleich sind (Bild 17.25b).
Im letzten Versuchsdurchgang lassen wir beide Spalte offen. Die Bälle kommen jetzt wahllos von Spalt 1 oder Spalt 2 zum Detektor. Die entstehende Verteilungskurve \(P_{12}\) ist die Summe der Verteilungen \(P_1\) und \(P_2\) (Bild 17.25c).
\[\begin{equation} P_{12} = P_1 + P_2 \tag{17.9} \end{equation}\]
17.3.2 Doppelspalt-Experimente mit klassischen Wellen
Als Nächstes führen wir den Doppelspalt-Versuch mit klassischen Wellen – zum Beispiel mit Wasserwellen – durch (Bild 17.26). Als Quelle verwenden wir einen punktförmigen Wellenerreger (1) in einem Wasserbecken. Nach dem Huygenssche Prinzip wird in jedem der beiden Spaltöffnungen (2) wieder eine Kreiswelle erzeugt. Der Detektor (3) dahinter misst die Intensität der ankommenden Wellen an den unterschiedlichen Stellen.
Im ersten Versuchsdurchgang schließen wir die untere Öffnung. Durch die Beugung am oberen Spalt erhalten wir die Intensitätsverteilung \(I_1\) (Bild 17.26, a).
Im zweiten Versuchsdurchgang öffnen wir die untere Öffnung und schließen die obere. Aufgrund der spiegelbildlichen Situation erhalten wir am Detektor die zu \(I_1\) symmetrische Intensitätsverteilung \(I_2\) (Bild 17.26, b).
Im dritten Versuchsdurchgang sind beide Spalte geöffnet. Die beiden Kreiswellen überlagern einander und wir erhalten am Detektor ein Interferenzmuster \(I_{12}\), mit einem Beugungsmaximum in der Mitte (Bild 17.26, c). Die Verteilung ist nicht mehr die Summe der Einzelverteilungen, lässt sich aber aus den beiden Einzelverteilungen mithilfe eines Interferenzterms ausdrücken:
\[\begin{equation} I_{12} = I_1 + I_2 + 2\cdot\sqrt{I_1\cdot I_2}\cdot\cos(\alpha) \tag{17.10} \end{equation}\]
Mit \(\alpha\), der Phasendifferenz zwischen den Wellenstrahlen.
17.3.3 Doppelspalt-Experimente mit Elektronen
Für den letzten Durchgang wählen wir als Quelle (1) eine Elektronenkanone, die Elektronen auf eine Blende mit zwei schmalen Spaltöffnungen (2) schießt. Als Detektor (3) wählen wir einen Teilchendetektor für Elektronen.
Beginnen wir zunächst mit jeweils nur einem geöffneten Spalt. Ist der obere Spalt offen, erhalten wir die aus dem Doppelspalt-Experiment mit klassischen Teilchen bekannte Verteilungskurve \(P_1\) (Bild 17.27, a). Ist nur der untere Spalt offen, erhalten wir am Detektor die Verteilung \(P_2\) (Bild 17.27, b).
Lassen wir beide Spalte offen, können wir feststellen, dass die Detektoren wie zuvor Elektronen zählen, aber es bildet sich allmählich ein Interferenzmuster aus (Bild 17.27, c)! Bild 17.28 zeigt den Schirm von vorn.
Die Formel für die Intensitätsverteilung am Doppelspalt bei Wellen kann auch für die Beschreibung des Interferenzmusters der Elektronen verwendet werden.
17.3.4 Interferenz durch Gedränge?
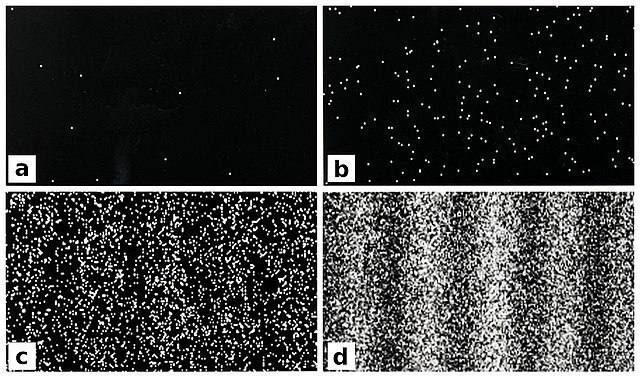
Versuchen wir, eine anschauliche Erklärung für das mysteriöse Interferenz-Verhalten der Elektronen zu finden. Vielleicht ist es ja ein Massenphänomen. Wenn sich viele Elektronen nahezu gleichzeitig durch die beiden Spalte bewegen, stoßen sie einander im Gedränge und bewirken dadurch vielleicht das Interferenzmuster? Wir können die Elektronenquelle so einstellen, dass nur alle paar Sekunden ein Elektron durch den Doppelspalt geschickt wird. Im Detektor hören wir nur alle paar Sekunden einen Klick. Trotzdem erhalten wir, wenn wir lange genug warten, wieder dasselbe Interferenzmuster, obwohl zur selben Zeit immer nur ein einziges Elektron unterwegs war. In Bild 17.29 siehst du das Ergebnis des Real-Doppelspalt-Experiments nach 11, 200, 6000 und 140000 Elektronen.
Es scheint, als würde jedes einzelne Elektron, wenn es durch die Blende hindurchgeht, „wissen“, ob ein oder beide Spalte offen sind und sich entsprechend anders verhalten – jedes einzelne Teilchen interferiert mit sich selbst!
17.3.5 Weg der Elektronen durch den Doppelspalt
Ein Gedränge als Ursache für das Interferenzmuster können wir ausschließen. Vielleicht teilt sich ja das Elektron in zwei Hälften, geht mit je einer Hälfte durch je einen Spalt. Danach vereinen sich beide Hälften wieder und kommen als ganzes Elektron am Detektor an. Oder vielleicht macht das Elektron einen Umweg, geht hintereinander durch beide Spalte durch und dann erst zum Detektor? Der Schlüssel zur Lösung scheint in der Frage zu liegen, welchen Weg das Elektron durch den Doppelspalt nimmt.
Um das zu untersuchen, ändern wir den letzten Doppelspalt-Versuch so ab, dass wir gleich hinter dem Spalt eine Lichtquelle montieren (Bild 17.30). Trifft gleich hinter dem Schirm ein Photon ein Elektron, können wir durch einen Lichtblitz erkennen, durch welchen der beiden Spalte es gekommen ist – analog der Sprühfarbe im Doppelspalt-Versuch mit klassischen Teilchen.
Wir stellen die Lichtquelle so ein, dass zu jedem Klick im Detektor ein Photon das Elektron „markiert“ – kein Elektron kommt unerkannt durch die Doppelspalt-Blende. Doch sobald wir Gewissheit haben, durch welchen Spalt jedes Elektron die Blende passiert, verhalten sich die Elektronen wie klassische Teilchen und das Interferenzmuster verschwindet. Das Elektron verhält sich radikal anders, wenn es mit anderen Objekten wechselwirkt oder anders ausgedrückt: „ob es beobachtet wird oder nicht“.
Es gibt keine Möglichkeit, das Verhalten der Elektronen beim Doppelspalt-Experiment durch einen bestimmten Weg durch die Versuchsanordnung zu erklären.
17.3.6 Beobachten, ohne zu stören
Offensichtlich stört die Wechselwirkung mit dem Photon das Elektron so sehr, dass es ein vollkommen anderes Verhalten zeigt, wie wenn es ohne Störung zum Detektor kommt. Besteht eine Möglichkeit, das Elektron zu sehen, ohne es zu stören?
Der Impuls eines Photons ist abhängig von seiner Wellenlänge (\(p=h/\lambda\)). Um ein „weicheres“ Licht zu erhalten, müssen wir die Frequenz vermindern (und damit die Wellenlänge erhöhen). Wir können zum Beispiel rötlicheres Licht, Infrarot oder sogar Radiowellen (Radar) verwenden. Im für unser Auge nicht sichtbaren Wellenlängenbereich bauen wir uns eine entsprechende Kamera, die uns die empfangene Information in ein Falschfarbenbild übersetzt. In Bild 17.31 siehst du, wie so eine Aufnahme für Radiowellen aussehen könnte.
Die Wellenlänge des Lichts entscheidet, bei welcher Entfernung zwei Punkte noch als getrennt gesehen werden können (Auflösungsvermögen). Wird die Wellenlänge des Lichts größer als die Entfernung der Spalte, sehen wir nur noch einen großen verschwommenen Blitz, wenn ein Photon auf ein Elektron trifft. Wir erkennen ein Elektron, können aber nicht mehr eindeutig sagen, durch welchen Spalt es gekommen ist. Und genau ab diesem Moment ist die Beeinflussung der Photonen so klein, dass die Elektronen beginnen, Interferenz zu zeigen. Verringern wir die Frequenz des Lichtes immer weiter, wird die Störung immer kleiner, bis wir wieder die Interferenz-Verteilung aus dem ungestörten Doppelspalt-Experiment mit Elektronen erhalten.
Es gibt keine Möglichkeit, die Elektronen zu beobachten, ohne gleichzeitig das Interferenzmuster zu stören.
17.3.7 Quantenobjekt – weder Teilchen noch Welle
Die Experimente in diesem und im letzten Kapitel zeigen, dass sich kleine Objekte (Atomgröße und darunter) weder durch das klassische Teilchenmodell noch durch das klassische Wellenmodell vollständig beschreiben lassen. Für diese Objekte benötigen wir ein neues Modell – das Modell des Quantenobjekts (engl. quantum mechanical object).
Auch wenn es uns schwerfällt: Wir müssen uns bei der Beschäftigung mit Quantenobjekten von vielen Vorstellungen aus dem Alltag trennen. Hier sind einige Beispiele:
Quantenobjekte verhalten sich zufällig. Für ein einzelnes Quantenobjekt gibt es keine konkrete Vorhersage. Aber eine große Zahl an gleichpräparierten Quantenobjekten folgt einem streng vorhersagbaren Muster. Etwas „erklären“ bedeutet auf Wahrscheinlichkeiten (Rechnung) oder relative Häufigkeiten (Experiment) zurückzuführen (statistische Kausalität).
Ein Quantenobjekt wird erzeugt und später mit einem Detektor gemessen. Dabei können wir nichts darüber aussagen, was das Quantenobjekt zwischen diesen beiden Ereignissen macht.
Ein Quantenobjekt hat keinen Ort, bevor es gemessen wird. Damit ist auch der Bahn-Begriff für Quantenobjekte nicht mehr anwendbar.
Allderings finden wir bei Quantenobjekten spannende neue Eigenschaften wie etwa die Verschränkung, die Nullpunktsenergie oder den Tunneleffekt, die es in der klassischen Physik nicht gibt.
Bisher haben wir Elektronen und Photonen immer als „Teilchen“ bezeichnet. Ab jetzt verwenden wir ausschließlich den neuen, korrekten Begriff Quantenobjekt.
17.3.8 Grenzen der Quantenmechanik
Du wirst jetzt die berechtigte Frage stellen, wo genau die Grenze zur klassischen Physik verläuft. Genauer gesagt: Ab welcher Größe verhält sich ein Objekt wie ein klassisches Teilchen?
Hier gibt es keine scharfe Grenze. Für größere Quantenobjekte nimmt die „Welligkeit“ des Interferenzmusters immer mehr zu (Bild 17.32). Die „Täler“ zwischen den „Bergen“ werden immer unbedeutender und die Einhüllende der Kurve (blau) bestimmt das Verhalten des Objekts. Die Form der Einhüllenden nähert sich zunehmend der Verteilung für klassische Teilchen.
Dass die Formeln der Quantenphysik für große Objekte in die Formeln der klassischen Physik übergehen, wird Korrespondenzprinzip (engl. correspondence principle) genannt.
17.3.9 Unschärferelation
In Bild 17.33 siehst du das Verhalten eines Strahls aus Quantenobjekten (zum Beispiel Photonen oder Elektronen). Ist der Spalt groß im Verhältnis zur Wellenlänge, bewirkt ein Verkleinern der Spaltbreite auch einen schmäleren Strahl. Sobald die Spaltbreite aber in die Größenordnung der Wellenlänge kommt, tritt Beugung auf. Jetzt weitet sich der Strahl wieder. Je enger die Öffnung, desto größer der Beugungseffekt.
Da wir wissen, dass ein Quantenobjekt durch den Spalt geht, wenn es am Schirm ankommt, ist die Spaltbreite ein Maß für die Genauigkeit der x-Koordinate des Quantenobjekts (die wir als quer zu Strahlrichtung wählen). Die Auffächerung des Strahls ist ein Maß für die Genauigkeit der Impulskomponente in x-Richtung. Durch Verkleinern der Blende kannst du die Genauigkeit für den Ort beliebig verbessern. Allerdings bewirkt die Beugung, dass bei zu engen Spaltbreiten die Genauigkeit der Impulskomponente in x-Richtung sich verschlechtert. In dieselbe Richtung sind beide Größen nicht beliebig genau anzugeben!
Messen wir konkret bei einer Vielzahl von gleich präparierten Quantenobjekten den Ort und den Impuls in Spaltrichtung, erhalten wir die Standardabweichungen \(\Delta x\) und \(\Delta p_x\) für die x-Position und den Impuls in x-Richtung. Diese Streuung der Messwerte wird als Unschärfe bezeichnet. Das Produkt aus Orts- und Impulsunschärfe kann nicht beliebig klein werden. Für alle Messungen gilt die Heisenbergsche Unschärferelation (engl. uncertainty principle, nach Werner Heisenberg):
| \[\begin{equation} \Delta x \cdot \Delta {p_x} \ge \frac{h}{{4\cdot\pi }} \tag{17.11} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(\Delta x\), die Ortsunschärfe in x-Richtung (in \(\text{m}\))
- \(\Delta p_x\), die Impulsunschärfe in x-Richtung (\(\text{kg}\cdot\frac{\text{m}}{\text{s}}\))
- \(h\), das Plancksche Wirkungsquantum (eine Konstante mit dem Wert \(6{,}6\cdot 10^{-34}\;\mathrm{Js}\))
Beachte, dass die Unschärferelation nur für Größen in dieselben Raumrichtung gilt. Der Ort in x-Richtung und der Impuls in y-Richtung können für ein Quantenobjekt zum Beispiel beliebig genau bestimmt sein!
Paare von Eigenschaften, die der Unschärferelation unterliegen, werden als komplementäre Eigenschaften eines Quantenobjekts bezeichnet.
Die Unschärferelation ist keine Folge von ungenauen Messinstrumenten, sondern eine Folge der Welleneigenschaft von Quantenobjekten. Sie ist daher eine prinzipielle Schranke der Natur.
17.3.10 Unschärferelation für Energie und Zeit
Ein weiteres Beispiel für komplementäre Eigenschaften ist die Energie eines Quantenobjekts in einem Zeitintervall. Die Unschärferelation für Energie und Zeit lautet:
| \[\begin{equation} \Delta E \cdot \Delta t \ge \frac{h}{4\cdot\pi} \tag{17.12} \end{equation}\] |
Diese Relation besagt, dass wir die Energie eines bestimmten Zustands umso besser bestimmen können, je länger wir Zeit für die Messung haben.
Aus klassischer Sicht kann die Unschärferelation für Energie und Zeit so interpretiert werden: Für eine kurze Zeit \(\Delta t\) darf ein Quantenobjekt die Energieerhaltung im Ausmaß von
\[\begin{equation} \Delta E\approx\frac{h}{4\cdot\pi\cdot\Delta t} \tag{17.13} \end{equation}\]
sogar verletzen.
17.3.11 Abschätzen der Unschärferelation
Die Unschärferelation können wir hier zwar nicht herleiten, aber wir können zumindest ihre Größenordnung abschätzen.
Wird ein Elektronenstrahl auf einen Spalt der Breite \(d\) gerichtet, kommt es zur Beugung, wenn die De-Broglie-Wellenlänge der Elektronen in der Größenordnung der Spaltbreite und darunter liegt. Für den Impuls eines Elektrons gilt \(p=h/\lambda\). Beschränken wir uns auf die Elektronen im Hauptmaximum (der Bereich zwischen dem linken und rechten 1. Minimum) des gebeugten Strahls (Bild 17.34). Für die Richtung zum ersten Beugungsminimum gilt:
\[ \sin(\alpha)=\frac{\lambda}{d} \]
Die meisten Elektronen werden innerhalb dieses Winkelbereichs am Schirm auftreffen. Ihre Impulskomponenten \(p_x\) quer zur ursprünglichen Strahlrichtung können positive und negative Werte annehmen und streuen mit der Größenordnung \(\Delta p_x\) um den Mittelwert null. Dann gilt:
\[ \Delta p_x \approx p\cdot\sin(\alpha) = p\cdot\frac{\lambda}{d} = \frac{h}{\cancel{\lambda}}\cdot\frac{\cancel{\lambda}}{d} = \frac{h}{d} \]
Die Ortsunschärfe \(\Delta x\) quer zur Strahlrichtung entspricht der halben Spaltbreite \(d\). Mit \(d=2\cdot\Delta x\) und wir erhalten
\[ \begin{aligned} \Delta p_x \approx {} & \frac{h}{2\cdot\Delta x} &&\qquad\Bigr\rvert\cdot \Delta x \\ \end{aligned} \]
und damit
\[ \Delta x\cdot\Delta p_x \approx \frac{h}{2} \]
Damit liegt unsere Abschätzung um den Faktor \(2\cdot\pi\) über dem Wert der Heisenbergschen Unschärferelation.
17.3.12 Freier Wille
In der klassischen Physik ist jede Teilchenbewegung durch die Bewegungsgesetze prinzipiell vorhersagbar. Nach dieser Vorstellung verhält sich das gesamte Universum wie ein riesiges Uhrwerk (Bild 17.35). Einem Wesen, das Kenntnis aller Teilchen und deren Anfangsbedingungen hat, wäre es demnach möglich, die Zukunft exakt vorherzusagen. Dieses gedachte Wesen wird nach Pierre-Simon Laplace (gesprochen „Laplas“ Audio abspielen ) als Laplacescher Dämon (engl. Laplace’s demon) bezeichnet. Unsere Zukunft wäre damit exakt vorherbestimmt (Determinismus). In der Praxis ist eine genaue Vorhersage dennoch sehr schwierig, weil sich die Anfangsbedingungen nicht genau messen lassen und kleine Variationen in den Anfangsbedingungen zu drastisch unterschiedlichen Entwicklungen führen können (Schmetterlingseffekt).
Das würde natürlich auch für uns Menschen gelten. Unsere Gedanken sind auch ein Zusammenspiel physikalischer Vorgänge. Damit wären alle unsere Gedanken vorherbestimmt und so etwas wie ein freier Wille ein Trugbild.
Die Quantenmechanik zeigt uns aber, dass im Mikrokosmos ganz andere Regeln gelten. Zum einen verhält sich ein einzelnes Quantenobjekt zufällig, auch wenn eine große Zahl gleichpräparierter Quantenobjekte sehr genauen statistischen Gesetzmäßigkeiten folgen. Zum anderen zeigt uns die Unschärferelation eine prinzipielle Schranke für die Genauigkeit einer Messung auf.
Es kann also nichts schaden, sein eigenes Schicksal in die Hand zu nehmen und seinen Lebensweg – respektvoll gegenüber der Natur und anderen Menschen – selbst zu gestalten.