17.6 Quantenobjekte in weiteren Potenzialen
In Bild 17.55 siehst du eine künstlich angefertigte kreisförmige Struktur aus 48 Kobalt-Atomen auf einer Kupferoberfläche.
Beim Beispiel eines Teilchens in einer Box hast du im letzten Kapitel gesehen, wie die Schrödingergleichung und die Normbedingung verwendet werden, um die Wahrscheinlichkeitsdichte-Funktion \(\psi^2\) bei einer vorgegebenen Potenzialfunktion für ein Quantenobjekt zu erhalten.
In diesem Kapitel werden wir uns das Verhalten von Quantenobjekten in weiteren Umgebungen ansehen, die realistischer als das unendliche Kastenpotenzial sind. Das Lösen der Schrödingergleichung für diese Potenziale ist allerdings wesentlich komplizierter als bei dem unendlichen Kastenpotenzial. Wir beschränken uns daher darauf, die Lösungen zu präsentieren und auf die daraus resultierenden erstaunlichen Effekte der Quantenwelt hinzuweisen. Und du wirst erfahren, wie es gelingt, so unfassbar kleine Strukturen wie die in Bild 17.55 herzustellen.
17.6.1 Harmonischer Oszillator in der Quantenmechanik
Mit dem harmonischen Oszillator haben wir uns schon in früheren Kapiteln sehr ausführlich beschäftigt. Er zeichnet sich durch eine Rückstellkraft aus, die proportional zur Auslenkung aus der Ruhelage ist (Hookesche Gesetz). Ein typisches Beispiel für einen harmonischen Oszillator ist eine Masse an einer Feder. Seine Potenzialfunktion ist eine quadratische Funktion (Bild 17.56).
Auch Atome und Moleküle verhalten sich unter bestimmten Umständen wie ein System aus Massen, die durch Schraubenfedern verbunden sind. Daher untersuchen wir ein Objekt in einem solchen Potenzial quantenmechanisch.
Die Wellenfunktionen (Lösungen der Schrödingergleichung) für einen harmonischen Quanten-Oszillator siehst du in Bild 17.57 auf der linken Seite. Sie sehen ähnlich aus wie die diskreten Lösungen beim unendlichen Kastenpotenzial, mit dem Unterschied, dass die Enden am Potenzialrand nicht abrupt auf null zurückgehen.

Bild 17.57: Lösungen des harmonischen Quanten-Oszillators (Wellenfunktion und Wahrscheinlichkeitsdichtefunktion)
In Bild 17.57 Mitte siehst du die entsprechenden Wahrscheinlichkeitsdichte-Funktionen. Je größer die Quantenzahl, desto größer die Energie und damit vergrößert sich auch der Bereich, in dem das Quantenobjekt angetroffen werden kann – so wie auch ein Federpendel mehr Platz zum Schwingen benötigt, je größer seine Energie ist.
In Bild 17.57 rechts sind die diskreten Energiewerte für die einzelnen Quantenzahlen aufgetragen. Wie beim unendlichen Kastenpotenzial ist auch die kleinste mögliche Energie nicht null (Nullpunktsenergie). Die darüber liegenden Energieniveaus befinden sich immer im gleichen Abstand – das ist charakteristisch für einen harmonischen Quanten-Oszillator.
In Bild 17.58 siehst du noch einmal die Antreffwahrscheinlichkeiten beim harmonischen Quanten-Oszillator für die Quantenzahlen \(n = 0, 1, 2, 3\) und \(10\). Die schwarz strichlierte Kurve zeigt die Antreffwahrscheinlichkeit für einen klassischen harmonischen Oszillator. Sie ist an den Umkehrpunkten am größten, weil die Geschwindigkeit an diesen Stellen am niedrigsten ist. Die größte Geschwindigkeit besitzt ein klassischer Oszillator beim Durchgang durch die Ruhelage – dort ist die Antreffwahrscheinlichkeit an Niedrigsten. Im Gegensatz dazu ist für den niedrigsten Energiezustand (\(n=0\)) die Antreffwahrscheinlichkeit für Quantenobjekte in der Mitte am größten!
Für steigende Quantenzahlen kannst du aber beobachten, dass die Welligkeit zunimmt und die Einhüllende sich der klassischen Vorhersage annähert – ein weiteres Beispiel für das Korrespondenzprinzip.
Die senkrechten orangen Striche zeigen die Lage der Umkehrpunkte für ein klassisches Teilchen mit derselben Energie. Die Wahrscheinlichkeitsdichte-Funktion für Quantenobjekte geht aber über diesen Bereich hinaus (schraffierte Fläche). Für Quantenobjekte gibt es also eine Wahrscheinlichkeit größer null, sie jenseits der klassischen Wendepunkte zu finden!
17.6.2 Endliches Rechteckpotenzial
Als Nächstes betrachten wir wieder ein Rechteckpotenzial, dieses Mal aber nicht mit unendlich starren Wänden, sondern mit einer „Tiefe“ \(B\). Für die ersten vier Quantenzahlen erhalten wir für das Potenzial in Bild 17.59 ähnliche Wellenfunktionen wie für das unendliche Kastenpotenzial, mit Ausnahme von den Randbereichen, bei denen es keine fixen Wellenknoten gibt – wie auch schon beim harmonischen Quanten-Oszillator.
In Bild 17.59 siehst du auf der rechten Seite die erlaubten Energiewerte. Die kleinste mögliche Energie ist nicht null (Nullpunktsenergie) und darüber finden sich wieder diskrete Energiewerte. Besitzt das Quantenobjekt eine Energie größer als \(B\) kann es den Potenzialtopf allerdings überwinden und ist frei (ungebunden). Es kann jeden beliebigen Energiewert darüber annehmen – die Energiewerte bilden ein Kontinuum. In solchen Fällen ist es üblich, den Nullpunkt der Energie so festzulegen, dass alle
- Energien gebundener Zustände negative und
- Energien ungebundener Zustände positive
Werte sind.
17.6.3 Rechteckiges Hindernis
In den bisherigen Beispielen in diesem Kapitel hast du immer wieder gesehen, dass Quantenobjekte in Bereichen anzutreffen sind, die nach der klassischen Physik absolut verboten sind. Das hat erstaunliche Konsequenzen für unser nächstes Beispiel. Wir betrachten ein rechteckiges Hindernis der Breite \(d\) und der Potenzialhöhe \(U_0\). Mit anderen Worten benötigt ein klassisches Teilchen mindestens eine Energie von \(U_0\), um das Hindernis überwinden zu können.
In Bild 17.60 siehst du die Lösung der Schrödingergleichung für ein Quantenobjekt. Obwohl die Energie \(E\) des Quantenobjekts unter der Potenzialhöhe \(U_0\) liegt, gibt es trotzdem eine Wahrscheinlichkeit größer null, das Quantenobjekt auf der anderen Seite der Barriere anzutreffen! Ein Teil der Quantenobjekte durchdringt den Energiewall, als gäbe es für sie einen Tunnel durch das Hindernis. Dieses in der klassischen Physik unmögliche Phänomen wird daher Tunneleffekt (engl. qunatum tunneling) genannt. Der Tunneleffekt erklärt zum Beispiel den spontanen Alphazerfall radioaktiver Atome und bildet die Grundlage für das Rastertunnelmikroskop.
Wie groß ist die Wahrscheinlichkeit, dass ein Quantenobjekt das Hindernis durchdringt? Innerhalb des endlichen Potenzial-Walls wird die Wellenfunktion durch eine abfallende Exponentialfunktion beschrieben, die im Wesentlichen die Form
\[\begin{equation} e^{-\frac{\displaystyle \sqrt{2\cdot m\cdot(U_0-E)} \cdot d}{\displaystyle \hbar}} \tag{17.28} \end{equation}\]
hat. Daraus kannst du sehen, dass die Wahrscheinlichkeit des Durchkommens umso größer ist, je
- kleiner die Masse \(m\) des Quantenobjekts
- kleiner die Höhe des Potenzial-Walls \(U_0\)
- kleiner die Dicke des Potenzial-Walls \(d\) und
- größer die Energie \(E\) des Quantenobjekts
ist. Der Tunneleffekt ist somit auf den Bereich von Quantenobjekten beschränkt!
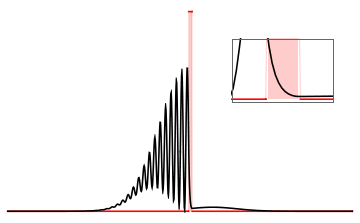
Während du auf der linken Seite eine stehende Welle hast, befindet sich nach dem Hindernis eine nach rechts fortschreitende Welle. Das kannst du an der Wahrscheinlichkeitsdichtefunktion \(\psi^2(x)\) erkennen: Während die Welligkeit vor dem Hindernis erhalten bleibt, ist nach dem Hindernis keine Welligkeit mehr zu sehen und die Antreffwahrscheinlichkeit ist gleichverteilt. Als Ergänzung siehst du in Bild 17.61 noch den Tunneleffekt für einen Wellenpuls, der auf ein Hindernis trifft.
Verletzt der Tunneleffekt nicht die Energieerhaltung? Die Energieerhaltung ist auch in der Quantenmechanik gültig. Allerdings gilt für Quantenobjekte auch die Unschärferelation. Weder Ort noch Impuls sind für ein Quantenobjekt genau bestimmt. Innerhalb dieser Grenzen lassen sich über ein Quantenobjekt keine genauen Aussagen machen. In diesem Ausmaß können die klassische Energie- und Impulserhaltung in der Quantenphysik verletzt werden.
17.6.4 Rastertunnelmikroskop
Beim Rasterelektronenmikroskop wurde das Auflösungsvermögen erhöht, in dem statt sichtbaren Lichts ein Elektronenstrahl verwendet wurde. Die De-Broglie-Wellenlänge kann zwar prinzipiell durch eine Beschleunigungsspannung beliebig klein gemacht werden, allerdings wird dabei auch der Impuls immer größer. Hochenergetische Elektronen dringen tief in das zu untersuchende Material ein. Damit lässt sich zwar die innere Struktur der Materie untersuchen, über die Oberfläche eines Materials erhalten wir so keine Information.
Beim Rastertunnelmikroskop RTM (engl. scanning tunneling microscope (STM)) wird der Tunneleffekt ausgenutzt, um Oberflächendetails bis auf Atomgröße abzubilden (Auflösung rund \(0{,}1\;\mathrm{nm}=10^{10}\;\mathrm{m}\)). Es wurde von Gerd Binnig und Heinrich Rohrer erfunden (Nobelpreis 1986).
In der klassischen Physik sind die Elektronen an ihre Atome gebunden. In der Quantenmechanik gibt es nur Antreffwahrscheinlichkeiten für Elektronen. Elektronen können mit einer geringen Wahrscheinlichkeit auch außerhalb ihrer Atomhülle angetroffen werden. Jedes Material umgibt daher eine „Wolke“ aus Elektronen, die mit der Entfernung von der Oberfläche exponentiell abnimmt (Bild 17.62). Das Rastertunnelmikroskop besteht aus einer extrem spitzen Nadel (ihre Spitze besteht nur aus einem einzelnen Atom!), die sich in einer Entfernung von weniger als \(1\;\mathrm{nm}\) von der Oberfläche befindet. Dabei überlappen einander die Elektronenwolken von Nadel und Oberfläche. Wird eine elektrische Spannung angelegt, kommt es zu einem messbaren Tunnelstrom. Die Nadel wird zeilenweise über die Oberfläche geführt, wobei ein Rückkopplungsmechanismus dafür sorgt, dass durch Heben und Senken der Nadel der Tunnelstrom konstant bleibt. Die Nadel zeichnet also das Relief der Oberfläche nach. Eine andere Möglichkeit besteht darin, die Nadel auf gleicher Höhe zu lassen und die Veränderung des Tunnelstromes zu messen, um so die Kontur der Oberfläche zu erhalten. In Bild 17.55 am Kapitelanfang siehst du das Ergebnis, nachdem diese Höheninformation mithilfe eines Computerprogramms in ein dreidimensionales Reliefbild umgewandelt und eingefärbt wurde.
Ein Rastertunnelmikroskop lässt sich aber auch für die Manipulation von Oberflächen verwenden. Dabei wird die Nadel als Kran verwendet, um einzelne Atome gezielt auf einer Oberfläche anzuordnen. So ist der Ring aus Kobalt-Atomen am Kapitelanfang (17.55) hergestellt worden.
Links:
- Video: Quantum tunnel effect and tunneling microscope
- Video: A Boy And His Atom: The World’s Smallest Movie (Stop-Motion-Film mit Kohlenmonoxid-Molekülen erstellt mit einem Rastertunnelmikroskop)
17.6.5 Tunneleffekt bei Atomkernen
In Bild 17.63 siehst du die vereinfachte Potenzialfunktion für ein Alpha-Teilchen innerhalb eines Atomkerns. Die Messung der Energie des Alpha-Teilchens nach einem Alphazerfall zeigt, dass seine Gesamtenergie zu klein ist, die Kernkraft (starke Wechselwirkung) zu überwinden und den Kern zu verlassen. Nach dem quantenmechanischen Tunneleffekt gibt es aber schon bei einer niedrigeren Energie eine gewisse Wahrscheinlichkeit, durch den Potenzialwall zu „tunneln“ und so aus dem Kern zu entweichen. Jetzt ist auch klar, warum der Zerfall eines radioaktiven Kerns zufällig passiert – es handelt sich um einen quantenmechanischen Effekt.
Auch die umgekehrte Richtung ist möglich. Der Verlauf der Potenzialfunktion für zwei Deuterium-Kerne hat eine ähnliche Form wie die Potenzial-Kurve in Bild 17.63. Nach der klassischen Physik ist die Energie der Deuterium-Kerne im Inneren der Sonne zu klein, um die elektrostatische Abstoßung zu überwinden, und es sollte nie zu einer Fusionsreaktion kommen. Nach der Quantenmechanik besteht aber auch für Deuterium-Kerne mit dieser niedrigen Energie eine gewisse Wahrscheinlichkeit, durch den Potenzialwall zu „tunneln“ und so zu fusionieren. Es braucht also die Quantenmechanik, um zu verstehen, warum die Sonne scheint.