16.7 Umwandlung von Masse und Energie
Die Formel für die Äquivalenz von Masse und Energie folgt aus den Annahmen der speziellen Relativitätstheorie. Ob und wie Masse und Energie ineinander umgewandelt werden können, verraten uns die Gleichungen nicht. Dass eine solche Umwandlung tatsächlich möglich ist, hat die Entwicklung der ersten Kernwaffen 1945 im Rahmen des Manhattan-Projekts eindrucksvoll bewiesen (Bild 16.61).
Die Wissenschaftsethik hat durch diese Entwicklung einen ganz neuen Stellenwert in der Physik erhalten. Keine bisherige physikalische Erkenntnis hatte das Potenzial, einen so großen Schaden anzurichten. Diesen Konflikt von Forscherdrang einerseits und der Verantwortung gegenüber der Menschheit und der Umwelt andererseits hat der Schriftsteller Friedrich Dürrenmatt in seinem Theaterstück „Die Physiker“ zum Thema gemacht.
Links:
16.7.1 Massendefekt
Wird die Masse eines Atomkerns mit der Summe der Massen der enthaltenen Kernteilchen verglichen, stellt sich heraus, dass der Atomkern eine geringere Masse hat als seine Bestandteile (Bild 16.62). Diese Massendifferenz zwischen gebundenen und ungebundenen Kernteilchen wird Massendefekt (engl. mass defect) genannt. Im Gegensatz zu dem Zitat von Aristoteles ist das Ganze sogar weniger als die Summe seiner Teile – zumindest was die Masse betrifft.
Berechnen wir die Massendifferenz von einem Helium-Kern und jeweils zwei Protonen und Neutronen, erhalten wir den Wert
\[ \begin{aligned} \Delta m = {} & m_{\text{He-4}}-2\cdot (m_p+m_n) \\ = {} & 6{,}64\ldots\cdot 10^{-27}\;\mathrm{kg}-2\cdot (1{,}67\ldots\cdot 10^{-27}\;\mathrm{kg}+1{,}67\ldots\cdot 10^{-27}\;\mathrm{kg}) \\ = {} & 6{,}64\ldots\cdot 10^{-27}\;\mathrm{kg}-6{,}69\ldots\cdot 10^{-27}\;\mathrm{kg} \\ = {} & -5{,}04\ldots\cdot 10^{-29}\;\mathrm{kg} \\ \end{aligned} \]
Die dieser Masse äquivalente Energie kannst du mit der Formel für die Ruhe-Energie berechnen.
\[ E=m\cdot c^2= 5{,}04\ldots\cdot 10^{-29}\;\mathrm{kg} \cdot (3\cdot 10^{8}\;\mathrm{m/s})^2 = 4{,}53\ldots\cdot 10^{-12}\;\mathrm{J} \]
Drücken wir das Ergebnis in der Einheit Elektronenvolt aus, kannst du sehen, dass dies für atomare Größenordnungen eine ungeheuer große Energiemenge ist.
\[ E=4{,}53\ldots\cdot 10^{-12}\;\mathrm{J}=28\,373\,348\;\mathrm{eV}=28{,}37\ldots\;\mathrm{MeV} \]
16.7.2 Bindungsenergie
Was ist mit der fehlenden Masse beim Massendefekt passiert? Die dieser Masse äquivalente Energie wurde bei der Erzeugung des Atomkerns in Form von Energie abgestrahlt. Willst du umgekehrt den Atomkern in seine Kernteilchen vollständig zerlegen, muss dieselbe Energiemenge wieder aufgebracht werden.
Diese Energie, die notwendig ist, die Bindung von Teilchen aufzubrechen, wird daher Bindungsenergie (engl. binding energy) genannt. Massendefekt und Bindungsenergie kommen bei jedem gebundenen System von Teilchen vor. So zum Beispiel auch bei chemischen Bindungen oder den Van-der-Waals-Kräften. Im Gegensatz zu Atomkernen ist der Massendefekt bei diesen gebundenen Systemen nahezu unmessbar klein. Denn es gilt:
| Je kleiner ein gebundenes System von Teilchen, desto größer ist die Bindungsenergie. |
In Bild 16.63 siehst du Beispiele für gebundene Systeme und die Größenordnung ihrer Bindungsenergien (Beachte, dass die Skala logarithmisch ist!).
Grund dafür ist die Nullpunktsenergie, die du im Kapitel Quantenmechanik kennenlernen wirst.
16.7.3 Kerne spalten oder vereinen
Es gibt ein allgemeines Prinzip der Natur: Ein System nimmt von allein immer den Zustand kleinster Energie an. Im Atomkern wirken aber zwei Kräfte mit sehr unterschiedlichen Eigenschaften (Bild 10.52):
- die über größere Entfernung wirkende elektrische Abstoßung zwischen allen Protonen und
- die anziehende starke Wechselwirkung, die nur zwischen benachbarten Kernteilchen wirksam ist
Die Stabilität einer Kernsorte hängt wesentlich von der Kerngröße ab. Aufgrund der wirkenden Kräfte, der Teilchenanordnung im Kern und anderer Effekte sind Eisen-Kerne die stabilsten Kerne. Willst du bei einem Eisen-Kern Nukleonen hinzufügen oder entfernen, ist dazu immer ein Netto-Energieaufwand nötig. Im Bild 16.64 siehst du eine mechanische Analogie. Dabei ist der vorhin erwähnte Energieaufwand als Höhe im Gelände angedeutet.
Die oberste Geländeform zeigt die Verhältnisse bei einem großen Kern. Ein Uran-Kern entspricht bei dieser Analogie einem großen Wassertropfen in der Mitte des Geländes. Wird dieser mit einem Messer geteilt, fallen beide Hälften in weiterer Folge von selbst in die Gruben niedriger Energie.
In der untersten Geländeform siehst du die Verhältnisse bei kleinen Kernen. Entsprechen die Tropfen zwei Wasserstoff-Kernen und geben wir ihnen einen kleinen Schubs zur Mitte, vereinigen sich die beiden Tropfen zu einem größeren. Nach der Vereinigung befindet sich das Wasser auf einem niedrigeren Energieniveau.
16.7.4 Bindungsenergie pro Nukleon
Im Abschnitt Massendefekt haben wir die Massendifferenz von Kern und Kernbestandteilen für einen Helium-4 Kern (Alphateilchen) berechnet. Teilst du diese Energie noch durch die Anzahl der Kernteilchen, erhältst du eine wichtige Größe – die Bindungsenergie pro Nukleon. Für unser Beispiel beträgt dieser Wert
\[ \frac{\Delta m_{\text{He-4}}}{4}= \frac{28{,}37\ldots\;\mathrm{MeV}}{4}= 7{,}09\ldots\;\mathrm{MeV} \]
Trägst du diesen Wert mit aufsteigender Massenzahl für die wichtigsten Isotope in ein Diagramm ein, erhältst du den Verlauf in Bild 16.65. In der Form der Kurve spiegelt sich das Wechselspiel von elektrischer Kraft und starker Wechselwirkung bei den einzelnen Kerngrößen wider.
Beginnst du links bei den leichten Kernen, steigt die Bindungsenergie pro Nukleon. In diesem Bereich kann durch Kernverschmelzung (Kernfusion) zu schwereren Kernen Energie gewonnen werden. Die Kurve im Diagramm steigt bis zum Eisen-Kern \(\text{Fe-56}\) und hat dort ein Maximum. Im Bereich zwischen Eisen und schwereren Kernen sinkt die Bindungsenergie pro Nukleon und die Kurve hat eine negative Steigung. In diesem Bereich kann durch Kernspaltung (Fission) von sehr schweren zu leichteren Kernen Energie gewonnen werden.
Ist von Kernenergie (engl. nuclear energy) die Rede, ist immer die Freisetzung der Bindungsenergie von Atomkernen gemeint.
Links:
16.7.5 Kernspaltung
Fängt ein Uran \(\text{U-235}\) Kern ein langsames Neutron ein, wird er kurzfristig zu einem \(\text{U-236}\) Kern. Dieser Kern ist instabil und zerfällt in kürzester Zeit (rund \(10^{-12}\;\mathrm{s}\)) auf mehrere mögliche Arten. Es entstehen zwei kleinere radioaktive Tochterkerne und mehrere einzelne Neutronen. Solche Zerfälle werden als Kernspaltung oder Fission (engl. nuclear fission) bezeichnet. Die frei werdenden Bindungsenergie wird in Bewegungsenergie der Spaltprodukte umgewandelt.
Im Bild 16.66 siehst du als Beispiel den Zerfall eines Uran-235 Kerns in einen Barium-144 und einen Krypton-89 Kern sowie drei Neutronen.
\[ \mathrm{n}+{}^{235}_{\,\,92}\mathrm{U}\ \longrightarrow\ {}^{144}_{\,\,56}\mathrm{Ba} +{}^{89}_{36}\mathrm{Kr} +3\mathrm{n} \]
Den Prozess des Spaltens kannst du dir wie bei einem schwingenden Flüssigkeitstropfen vorstellen (Tröpfchenmodell). Dabei gerät der instabile Kern zunächst in Schwingungen und die Tochterkerne trennen sich ähnlich Flüssigkeitstropfen voneinander.
Im Diagramm 16.65 kannst du sehen, dass ein Kern mit 236 Nukleonen eine Bindungsenergie von \(7{,}6\;\mathrm{MeV}\) pro Nukleon besitzt. Zerfiele er beispielsweise in zwei gleich große Tochterkerne, bestünde jeder von ihnen aus \(236/2=118\) Nukleonen mit einer Bindungsenergie von \(8{,}5\;\mathrm{MeV}\) pro Nukleon. In den Tochterkernen ist daher jedes Nukleon um \(0{,}9\;\mathrm{MeV}\) (\(=8{,}5\;\mathrm{MeV}-7{,}6\;\mathrm{MeV}\)) stärker gebunden als im Mutterkern. Bei diesem Zerfall würde also insgesamt \(236\cdot 0{,}9\;\mathrm{MeV} = 212{,}4\;\mathrm{MeV}\) Bindungsenergie frei. Das ist eine ungeheuer große Menge Energie für eine einzige Reaktion. Bei einer typischen chemischen Reaktion werden nur wenige Elektronenvolt pro Atom freigesetzt. Das ist also etwa 100 Millionen Mal (\(10^{8}\)) weniger Energie!
16.7.6 Kettenreaktion
Die bei der Kernspaltung frei werdenden Neutronen können ihrerseits weitere Kernzerfälle auslösen. Bei der Spaltung von Uran-235 entstehen durchschnittlich \(2{,}47\) freie Neutronen. Befinden sich ausreichend spaltbare Kerne in der Umgebung, kommt es zu einer Kettenreaktion und die Anzahl der Spaltungen wächst exponentiell mit der Zeit (Bild 16.67). Eine solche Menge wird als überkritische Masse bezeichnet.
In den meisten Fällen ist eine anhaltende Kettenreaktion mit konstanter Reaktionsrate erwünscht. Ist dieser Zustand erreicht, lösen die bei einer Spaltung frei werdenden Neutronen durchschnittlich genau eine weitere Spaltung aus (Multiplikationsfaktor ist gleich 1). Diese Menge wird als kritische Masse (engl. critical mass) bezeichnet.
Bei einer unterkritischen Masse schließlich nimmt die Anzahl der Kernspaltungen mit der Zeit ab, bis es zu keinen weiteren Spaltungen mehr kommt.
16.7.7 Kernreaktor
Ein Kernkraftwerk wandelt die frei werdende Energie bei der Kernspaltung in elektrische Energie um. In Bild 16.68 siehst du den Aufbau eines Reaktordruckbehälters, wie er in einem Siedewasserreaktor – die einfachste Bauform eines Kernkraftwerks – vorkommt.
Im Reaktorkern befinden sich die Brennelemente mit den einzelnen Brennstäben, die das spaltbare Material (zum Beispiel \(\text{U-235}\)) in gebundener Form enthalten („Brennen“ ist hier nicht im chemischen Sinn gemeint). Die bei der Kernspaltung frei werdende Energie erhitzt das umgebende Wasser und lässt es verdampfen. Mithilfe des Wasserdampfes wird dann – wie in einem Kohle- oder Gaskraftwerk – über eine Dampfturbine elektrische Energie gewonnen.
Das Wasser erfüllt aber auch noch eine zweite Aufgabe. Die bei der Spaltung entstehenden Neutronen sind zu schnell, um von den Urankernen eingefangen zu werden und so weitere Spaltungen auszulösen. Durch Stöße mit den Wassermolekülen verlieren sie an Bewegungsenergie. Das Wasser dient als Moderator, der die Neutronen für die Spaltung abbremst.
Um die Anzahl der Spaltungen pro Sekunde konstant zu halten und eine unkontrollierte Kettenreaktion zu verhindern, gibt es bewegliche Steuerstäbe. Sie bestehen aus einem Material, das Neutronen absorbiert, sodass sie nicht für weitere Kernspaltungen zur Verfügung stehen.
Alle Reaktoren, die nach dem oben beschriebene Prinzip arbeiten, werden thermische Reaktoren (engl. thermal-neutron reactor) genannt. Ein anderer Reaktor-Typ ist der Brutreaktor (engl. breeder reactor), der ohne Moderator auskommt und „schnelle Neutronen“ zur Spaltung verwenden kann. In diesem wird nicht nur Kernenergie gewonnen. Gleichzeitig werden auch nicht spaltbare Nuklide (zum Beispiel das häufig vorkommende Isotop \(\text{U-238}\)) in spaltbares Material umgewandelt. Dabei wird sogar mehr Kernbrennstoff erzeugt, als verbraucht wird! Bei der Kernenergie wären wir also nicht auf die beschränkten natürlichen Uran \(\text{U-235}\) Vorkommen angewiesen, sondern könnten Kernbrennstoff selbst herstellen. Leider birgt diese Technologie nicht nur zusätzliche Sicherheitsrisiken – diese Art von Reaktor wird auch zur Herstellung von Kernwaffen benutzt.
In Oklo (Westafrika) wurde sogar ein natürlicher Kernspaltungsreaktor entdeckt. An dieser Stelle befand sich Uranerz in passender Konzentration und Menge, sowie Grundwasser als Moderator, sodass zu einer selbsterhaltenden Kernspaltung über einen längeren Zeitraum kommen konnte.
16.7.8 Tscherenkow-Strahlung
Wasser hat einen Brechungsindex von rund \(1{,}33\). Damit beträgt die Lichtgeschwindigkeit in Wasser „nur“ etwa \(75\,\%\) der Vakuumlichtgeschwindigkeit. In einem Kernspaltreaktor wird Wasser als Moderator für die Verlangsamung der Neutronen verwendet. Im Betrieb entstehen teilweise extrem schnelle Elektronen. Zum Beispiel durch den Beta-Zerfall von Spaltprodukten oder durch Gamma-Strahlung und darauffolgender Compton-Streuung. Die Geschwindigkeit einiger dieser Elektronen ist sogar größer als die Lichtgeschwindigkeit im Wasser (aber immer noch kleiner als die Vakuumlichtgeschwindigkeit).
Befinden sich Atome entlang der Bahn freier Elektronen, bewirkt ihre negative Ladung eine kurzzeitige Verschiebung der Hüllenelektronen. Bei langsamen Elektronen löschen sich die Wellen von benachbarten Atomen durch destruktive Interferenz aus. Bei Störungen des elektromagnetischen Feldes, die durch überlichtschnelle Elektronen verursacht werden, überlagern sich die Wellenfronten wie bei einem Mach-Kegel, wenn sich Körper schneller als mit Überschallgeschwindigkeit bewegen. Diese Strahlung ist als bläuliches Licht zu sehen (Bild 16.69).
Diese Strahlung wird nach Pawel Alexejewitsch Tscherenkow, der als erster schnelle Elektronen als Ursache für das blaue Leuchten vermutete, Tscherenkow-Strahlung (engl. Cherenkov radiation) genannt.
16.7.9 Wirkungsquerschnitt
Die Wahrscheinlichkeit für ein Neutron von einem Uran-235 Kern aufgenommen zu werden und in der Folge eine Kernspaltung auszulösen ist geschwindigkeitsabhängig. Je kleiner die Geschwindigkeit, desto mehr Zeit gibt es für eine Wechselwirkung zwischen Neutron und Kern und umso wahrscheinlicher der Einfang.
Je größer ein Ziel, desto wahrscheinlicher treffe ich es bei einem zufälligen Schuss. Diese anschauliche Vorstellung liegt der Angabe der Wahrscheinlichkeit für einen Neutroneneinfang durch den sogenannten Wirkungsquerschnitt des Neutrons (engl. neutron cross section) zugrunde. In Bild 16.70 siehst du die Wirkungsquerschnitte der Uranisotope für rasche (a) und langsame (b) Neutronen angedeutet. Rote Kreise entsprechen U-235 Kernen, dunkelrote Kreise entsprechen U-238 Kernen. Mit sinkender Geschwindigkeit nimmt die „Trefferfläche“ für die Neutronen zu. Der Begriff des Wirkungsquerschnitts ist ein praktisches Maß für die Berechnungen bei Kernreaktionen.
Die Ursache für die geschwindigkeitsabhängige Einfangwahrscheinlichkeit ist die Kernkraft, die nur auf sehr kurze Distanzen wirkt. Die Abbildung soll nur den Begriff des Wirkungsquerschnitts verdeutlichen. Bitte beachte, dass die Uran-235-Isotope zu keiner Zeit ihre Größe ändern!
16.7.10 Kernspaltungsbombe
Unter dem umgangssprachlichen Begriff „Atombombe“ ist in den meisten Fällen eine Kernwaffe gemeint, die nach dem Prinzip der Kernspaltung funktioniert. In Bild 16.71 siehst du ihren schematischen Aufbau.
Im Inneren befinden sich zwei Hälften eines spaltbaren Materials (zum Beispiel Plutonium). Jede für sich bildet eine unterkritische Masse – es kann also von allein nicht zu einer Kettenreaktion kommen. Um das spaltbare Material herum befindet sich herkömmlicher Sprengstoff. Bei der Zündung explodiert der Sprengstoff und komprimiert die beiden Hälften zu einer überkritischen Masse. Jetzt beginnt die unkontrollierte Spaltungskettenreaktion und setzt die Energie frei. Bei der Explosion entsteht neben Hitze und der Druckwelle auch noch ionisierende Strahlung. Hat sich die Druckwelle entfernt, kühlt die Umgebung ab und der Feuerball beginnt sich aufgrund von Konvektion zu heben. Dabei reißt er Staub und Asche mit in die Höhe und die charakteristische Pilzwolke („Atompilz“) entsteht (Bild 16.61 am Kapitelanfang).
Die Sprengkraft der größten jemals gezündeten Kernspaltungsbombe beträgt etwa \(500\;\mathrm{kT}\) TNT-Äquivalent (\(\approx2\cdot10^{15}\;\mathrm{J}\)).
16.7.11 Kernverschmelzung
Im Diagramm zur Bindungsenergie pro Nukleon (Bild 16.65) sehen wir: Werden leichte Kerne miteinander verschmolzen, hat der neu entstandene Kern eine geringere Masse pro Nukleon als die Ausgangskerne. Die bei dieser Kernverschmelzung (Kernfusion) frei werdende Bindungsenergie wird in Bewegungsenergie der Teilchen umgewandelt.
In Bild 16.72 siehst du ein Beispiel für eine Kernfusion. Dabei wird Deuterium (\(\text{H-2}\)) und Tritium (\(\text{H-3}\)) zu einem Heliumkern (\(\text{He-4}\)) verschmolzen. Bei dieser konkreten Reaktion wird Bindungsenergie von
\[ 14{,}1\;\mathrm{MeV}+3{,}5\;\mathrm{MeV}=17{,}6\;\mathrm{MeV} \]
als Energie freigesetzt. Vergleichst du diese Fusionsenergie mit der von Helium zu Lithium oder der Energiefreisetzung bei der Kernspaltung, siehst du einen gewaltigen Unterschied. Durch die extreme Asymmetrie im Diagramm zur Bindungsenergie pro Nukleon ist die Verschmelzung der leichtesten Kerne die Methode mit dem größten Energiegewinn.
16.7.12 Fusionsreaktor
Dass die Kernfusion von Wasserstoff zu Helium ausgezeichnet funktioniert, zeigt uns die Sonne. Allerdings ist es eine sehr schwierige Aufgabe, die Bedingungen, die im Inneren eines Sternes zur Fusion von Kernen führen, auf der Erde nachzustellen. Obwohl seit den 1960er-Jahren versucht wird, einen wirtschaftlichen Fusionsreaktor (engl. fusion reactor) zu bauen, sind wir auch heute noch weit davon entfernt, Kernfusion als weiteren Energieträger nutzen zu können.
Wird Gas auf rund 100 Millionen Kelvin erhitzt. Bei diesen Temperaturen sind Elektronen und Atomkerne voneinander getrennt und können sich frei bewegen. Dieser Zustand wird als Plasma bezeichnet. Um den Fusionsprozess aufrechtzuerhalten, müssen diese geladenen Teilchen in einem eng begrenzten Raum über einen längeren Zeitraum zusammenzuhalten werden. Da kein Material dieser hohen Temperatur standhält, muss das Plasma dabei berührungslos in Schwebe gehalten werden.
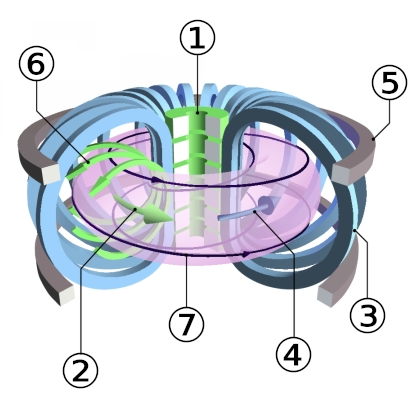
Eine mögliche Bauform wird Tokamak genannt. Hier wird das Plasma in einen torusförmigen Bereich eingeschlossen (Bild 16.73). Dafür induziert ein Transformator (1) zunächst einen ringförmigen Strom im Plasma (2). Nachdem der Plasmastrom gerichtet ist, wird er noch mithilfe eines Magnetfeldes eingeschnürt. Das Magnetfeld einer Wicklung um den Torus (3) reicht dafür aber nicht aus. Anders als bei der Bewegung geladener Teilchen in einem homogenen Magnetfeld würden die Ladungen im Torus bei ihrer schraubenförmigen Bahn nach außen driften. Um das zu verhindern, gibt es noch ein zweites Magnetfeld von ringförmigen Spulen am Umfang des Torus (5). Die Überlagerung ergibt ein Feld mit spiralförmigen Feldlinien (7). Um diese Feldlinien spiralen die geladenen Plasmateilchen aufgrund der Lorentzkraft und verbleiben innerhalb des Torus. Jede Änderung, wie das Einbringen von Material, erzeugt Verwirbelungen, die eine komplizierte Steuerung des Magnetfeldes ausgleichen muss.
Aktuell wird in Frankreich der internationale Versuchskernfusionsreaktor ITER (International Thermonuclear Experimental Reactor) gebaut, der nach dem Tokamak-Prinzip arbeitet. Er soll frühestens 2035 in Betrieb gehen.
Eine alternative Bauweise ist der Stellarator. Dabei ist kein Strom im Plasma selbst notwendig, und das Plasma wird stattdessen durch ein verdrilltes Magnetfeld eingeschlossen (Bild 16.74).
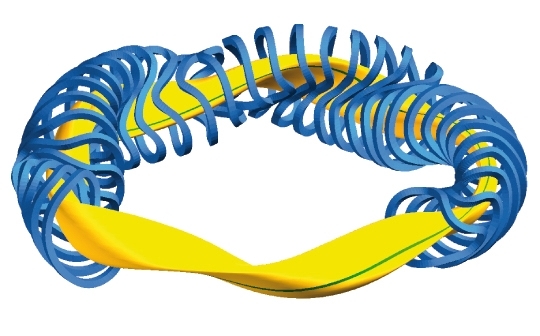
Bild 16.74: Experimenteller Fusionsreaktor Wendelstein 7-X
Beide Ansätze haben Vor- und Nachteile. Welche Bauweise zum ersten wirtschaftlichen Fusionsreaktor führen wird, ist heute noch nicht absehbar. Im Gegensatz zu Kernspaltreaktoren hätten Fusionsreaktoren enorme Vorteile: Eine Kernschmelze ist unmöglich und beim Betrieb entsteht weder waffenfähiges Material noch Atommüll mit langer Halbwertszeit.
16.7.13 Wasserstoffbombe
Eine Wasserstoffbombe ist eine Kernwaffe, die nach dem Prinzip der Kernfusion funktioniert. In Bild 16.75 siehst du den Aufbau und die Zündung einer solchen Bombe.
Die Bombe besitzt im oberen Teil eine Kernspaltbombe und im unteren Teil die eigentliche Fusionsladung. Das Zünden des Atomsprengsatzes erzeugt die notwendige Hitze, um das Material der Fusionsladung in den Plasmazustand zu versetzen und die Fusionsreaktion einzuleiten.
Die größte bisher gezündete Wasserstoffbombe (Zar-Bombe) hat eine Sprengkraft von rund \(50\;\mathrm{MT}\) TNT-Äquivalent (\(\approx2\cdot10^{17}\;\mathrm{J}\)) – also etwa das Hundertfache einer Kernspaltungsbombe.
16.7.14 Paarvernichtung
Die vollständige Äquivalenz von Masse und Energie zeigt sich beim Zusammentreffen eines Elektrons mit seinem Anti-Teilchen – einem positiv geladenen Elektron. So ein Teilchen wird Positron (oder „Anti-Elektron“) genannt und entsteht zum Beispiel beim Beta-Zerfall. Dabei wird die gesamte Masse beider Teilchen in Energie umgewandelt, indem zwei Gamma-Quanten (Lichtteilchen mit hoher Energie) abgestrahlt werden (Bild 16.76). Bei dieser Paarvernichtung oder Annihilation ist sowohl die Ladungserhaltung also auch die Impulserhaltung erfüllt – aus diesem Grund entstehen auch immer zwei Gamma-Quanten.
Die Summe der Energie der Gamma-Quanten lässt sich aus der Masse von Elektron und Positron mithilfe der Formel für die Ruhe-Energie berechnen.
\[ \begin{aligned} E = {} & m\cdot c^2 \\ = {} & 2\cdot m_e\cdot c^2 \\ = {} & 2\cdot 9{,}10\ldots\cdot 10^{-31}\;\mathrm{kg} \cdot (3\cdot 10^{8}\;\mathrm{m/s})^2 \\ = {} & 1{,}63\ldots\cdot 10^{-13}\;\mathrm{J} \\ = {} & 1{,}02\ldots\;\mathrm{MeV} \\ \end{aligned} \]
Diese (bezogen auf die beteiligte Masse) unglaublich große frei werdende Energiemenge hat schon viele Science-Fiction Schriftstellerinnen und Schriftsteller dazu inspiriert, die Vernichtung von Materie und Anti-Materie als Treibstoff für Raumschiffe in ihren Geschichten zu verwenden. Dabei gibt es aber zwei prinzipielle Probleme. Einerseits benötigt die aufwendige Herstellung von Anti-Materie ein Vielfaches der Energie, die dann wieder freigesetzt wird. Außerdem kann ein Tank aus Materie nicht für die Speicherung von Anti-Materie verwendet werden – jeder Kontakt würde eine Paarvernichtung auslösen. Die einzige Möglichkeit besteht darin, Anti-Materie berührungslos zu speichern, wie zum Beispiel in einer magnetischen Flasche oder einem Speicherring.
16.7.15 PET-Scanner
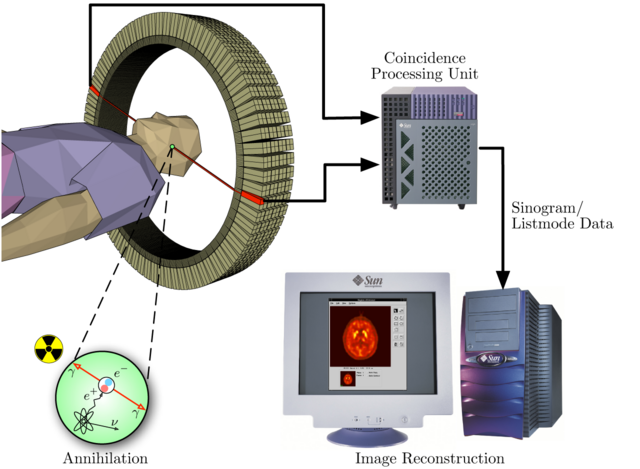
Obwohl Anti-Teilchen sehr exotisch klingen, ist die Entstehung von Positronen als Folge des Beta-Plus-Zerfalls ein alltägliches Phänomen und wird auch gezielt in der Medizin für Untersuchungen verwendet (Bild 16.77).
Vor der Untersuchung wird zunächst eine Flüssigkeit getrunken, die eine schwach radioaktiv markierte Substanz (Radiopharmakon) enthält. Beim Beta-Plus-Zerfalls im Körper und der anschließenden Paarvernichtung durch ein benachbartes Elektron entstehen gleichzeitig zwei Photonen, die sich in entgegengesetzter Richtung bewegen. Wenn diese beiden Photonen von zwei gegenüberliegenden Detektoren eines PET-Scanners (Positronen-Emissions-Tomographie) registriert werden, kann aus deren Richtung und Laufzeitdifferenz die exakte Position im Körper berechnet werden, an dem der Zerfall stattgefunden hat. So lassen sich etwa Zellen mit erhöhtem Stoffwechsel (darunter Krebszellen) in einem Organismus erkennen, wenn das Radiopharmakon nicht nur radioaktiv ist, sondern Teile enthält, die für den Stoffwechsel wichtig sind.
16.7.16 Paarbildung
Auch die Umkehrung der Paarvernichtung – die Paarbildung (engl. pair production) – kommt in der Natur vor. In Bild 16.78 siehst du ein Beispiel für eine Paarbildung: Trifft ein energiereiches Gamma-Quant auf einen Atomkern, kann ein Elektron-Positron Teilchenpaar entstehen. Auch bei diesem Vorgang ist sowohl die Ladungserhaltung als auch die Impulserhaltung erfüllt – der Kern übernimmt den restlichen Impuls.
Grundvoraussetzung für eine Paarbildung ist, dass die Energie des Gamma-Quants mindestens die Energie von \(1{,}02\ldots\;\mathrm{MeV}\) besitzt – also das im Abschnitt Paarvernichtung berechnete Masseäquivalent von Elektron- und Positron-Masse.