17.5 Teilchen in einem Kasten
In Bild 17.46 siehst du ein Teilchen, eingesperrt in einer Box.
Zunächst sehen wir uns die klassische Sichtweise für dieses Beispiel an, dann werden wir die Situation aus quantenmechanischer Sicht betrachten. Dabei wirst du sehen, wie die Schrödingergleichung verwendet wird, um die möglichen Zustände eines Quantenobjekts in der Box zu erhalten.
17.5.1 Klassische Betrachtung
In unserem idealisierten Beispiel bewegt sich ein Teilchen kräftefrei zwischen zwei (unendlich starren) Wänden hin und her. An den Wänden kommt es zu vollkommen elastischen Stößen. Es gilt die Energieerhaltung und Impulserhaltung. Das Teilchen hat zwischen den Wänden stets dieselbe konstante Geschwindigkeit.
Durch die konstante Geschwindigkeit ist das Teilchen gleich häufig an allen Stellen entlang des Weges anzutreffen. Die Wahrscheinlichkeit, das Teilchen an einem bestimmten Ort anzutreffen – die Antreffwahrscheinlichkeit – ist überall gleich groß.
Die kinetische Energie des Teilchens hängt – bei vorgegebener Masse – nur von der Geschwindigkeit ab und kann beliebige Werte annehmen.
Die kleinste mögliche Energie ist \(E_\text{KIN} = 0\).
Ort und Impuls des Teilchens sind beliebig genau messbar.
Das Teilchen kann nicht in die Mauer eindringen.
17.5.2 Unendliches Kastenpotenzial
Der Rest des Kapitels ist der quantenmechanischen Betrachtung gewidmet. Als ersten Schritt müssen wir die Potenzialfunktion – also die Kräfte, die auf das Quantenobjekt wirken – für die Box angeben (17.47).
Befinden sich die Wände in der Entfernung \(L\) und wählen wir die linke Wand als Bezugspunkt, lautet die Potenzialfunktion (unendliches Kastenpotenzial):
\[\begin{equation} \begin{aligned} U(x) = {} & \infty\qquad&&\text{für}\quad x < 0 \\ U(x) = {} & 0\qquad&&\text{für}\quad 0 < x < L \\ U(x) = {} & \infty\qquad&&\text{für}\quad x > L \\ \end{aligned} \tag{17.19} \end{equation}\]
Mit \(U(x) = \infty\) drücken wir aus, dass es unmöglich ist, dass das Quantenobjekt in die unendlich starren Wände eindringt.
17.5.3 Schrödingergleichung für ein Kastenpotenzial
Wir verwenden jetzt die zeitunabhängige Schrödingergleichung in einer Dimension:
\[ -{\frac {\hbar ^{2}}{2m}}\cdot{\frac {\mathrm {d} ^{2}\psi(x)}{\mathrm {d} x^{2}}} + U(x)\cdot\psi(x) = E\cdot\psi(x) \]
Da unser Quantenobjekt nicht in die Wände eindringen kann, ist die Wahrscheinlichkeit es außerhalb der Box anzutreffen null. Egal wie die Lösung \(\psi(x)\) auch aussehen mag, sie muss an den Stellen \(x=0\) und \(x=L\) zu null werden und überall außerhalb null bleiben. Innerhalb der Box gilt \(U(x) = 0\) und die Schrödingergleichung vereinfacht sich zu
\[\begin{equation} -{\frac {\hbar ^{2}}{2m}}\cdot{\frac {\mathrm {d} ^{2}\psi(x)}{\mathrm {d} x^{2}}} = E\cdot\psi(x) \tag{17.20} \end{equation}\]
17.5.4 Wellenfunktionen für ein Kastenpotenzial
Du kennst vermutlich kein systematisches Verfahren zur Lösung von Differenzialgleichungen, aber wir können versuchen, die Lösung zu erraten. Lassen wir einmal die konstanten Faktoren außer acht, besagt die Differenzialgleichung, dass die gesuchte Funktion gleich ihrer zweiten Ableitung sein muss. Diese Eigenschaft besitzen die Sinus- und Kosinus-Funktionen. Da außerdem \(\psi(0) = 0\) gefordert ist, wählen wir die allgemeine Sinusfunktion
\[\begin{equation} \psi(x) = A\cdot\sin(k\cdot x) \tag{17.21} \end{equation}\]
mit den Konstanten \(A\) und \(k\) als Lösungsansatz.
Um auch die Bedingung \(x=L\) zu erfüllen, muss das Argument der Sinusfunktion bei \(x=L\) ein Vielfaches von \(\pi\) sein, also \(k\cdot L=n\cdot\pi\), wobei \(n\) eine natürliche Zahl ist. Dann ist \(k=n\cdot \pi/L\), und unsere Lösungen haben die Form
\[\begin{equation} \psi(x) = A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right),\qquad n=1,2,3,\ldots \tag{17.22} \end{equation}\]
mit der Amplitude \(A\), die noch bestimmt werden muss.
Die Zahlen \(n=1,2,3,\ldots\) heißen Quantenzahlen (engl. quantum numbers) und kommen in jeder Lösung der Schrödingergleichung vor. In unserem einfachen, eindimensionalen Fall genügt eine einzige Quantenzahl, um den quantenmechanischen Zustand eines Objekts vollständig zu beschreiben. Im Allgemeinen sind dazu mehrere Quantenzahlen notwendig.
In Bild 17.47 die Potenzialfunktion für die ersten Quantenzahlen.
Im Kapitel über Teilchen mit Welleneigenschaften hast du von der Idee der Materie-Welle erfahren. Außerdem hast du im Teil über klassische Wellen gesehen, wie sich durch Überlagerung geeigneter fortschreitender Wellen sogenannte stehende Wellen (mit Wellenknoten und Wellenbäuchen) ausbilden können. In Analogie dazu kannst du dir die Wellenfunktionen, die als Lösungen der Wellenfunktionen auftreten, als eine Art „stehende Teilchenwelle“ vorstellen.
17.5.5 Einsetzen in die Schrödingergleichung
Als Nächstes setzen wir unseren Lösungsansatz in die Schrödingergleichung ein. Dazu benötigen wir die zweifache Ableitung von \(\psi(x)\):
\[ \begin{aligned} \psi(x) = {} & A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right) \\ \frac {\mathrm {d}\psi(x)}{\mathrm {d} x} = {} & \frac{n\cdot \pi}{L}\cdot A\cdot\cos\left(\frac{n\cdot \pi\cdot x}{L}\right) \\ \frac {\mathrm {d} ^{2}\psi(x)}{\mathrm {d} x^{2}} = {} & -\frac{n^2\cdot \pi^2}{L^2}\cdot A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right) \\ \end{aligned} \]
Setzen wir \(\psi(x)\) und \(\mathrm {d} ^{2}\psi(x)/\mathrm {d} x^{2}\) in die Schrödingergleichung ein, erhalten wir:
\[ \begin{aligned} \left(-{\frac {\hbar ^{2}}{2m}}\right)\cdot\left[-\frac{n^2\cdot \pi^2}{L^2}\cdot A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right)\right] = {} & E\cdot \left[A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right)\right] \\ {\frac {\hbar ^{2}}{2m}}\cdot \frac{n^2\cdot \pi^2}{L^2}\cdot A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right) = {} & E\cdot A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right) &&\Bigr\rvert:A\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right)\\ {\frac {\hbar ^{2}}{2m}}\cdot \frac{n^2\cdot \pi^2}{L^2} = {} & E \\ \end{aligned} \]
Also
\[\begin{equation} E = \frac{n^2\cdot\pi^2\cdot\hbar^2}{2\cdot m\cdot L^2} \tag{17.23} \end{equation}\]
17.5.6 Energiewerte für ein Kastenpotenzial
Die letzte Gleichung ((17.23)) besagt, dass unsere Wellenfunktionen tatsächlich eine Lösung der Schrödingergleichung für das unendliche Kastenpotenzial sind, allerdings für die Einschränkung auf bestimmte Energiewerte. Für diese Energiewerte gilt (mit \(\hbar =h/2\pi\)):
\[\begin{equation} E = \frac{n^2\cdot h^2}{8\cdot m\cdot L^2},\qquad n=1,2,3,\ldots \tag{17.24} \end{equation}\]
Daraus folgt:
- Das Quantenobjekt kann nur bestimmte diskrete Energiewerte annehmen
- Die kleinste mögliche Energie ist nicht null
Der quantenmechanische Zustand mit der niedrigsten Energie wird Grundzustand genannt. In unserem Beispiel entspricht das der Energie:
\[\begin{equation} E = \frac{h^2}{8\cdot m\cdot L^2} \tag{17.25} \end{equation}\]
In Bild 17.50 siehst du die Energiewerte für die ersten Quantenzahlen im Vergleich (die waagrechte Länge der roten Linien hat keine Bedeutung)
17.5.7 Nullpunktsenergie
Die kleinstmögliche Energie, die ein Quantenobjekt im Grundzustand annehmen kann, wird als Nullpunktsenergie (engl. zero-point energy) oder bezeichnet. Nach der klassischen Physik sollten alle Teilchenbewegungen aufhören, wenn sich die Temperatur dem absoluten Nullpunkt nähert. Nach der Quantenmechanik kann die Energie für ein Objekt aber niemals null werden.
Warum kann die Energie niemals null werden? Wäre die Energie eines Quantenobjekts gleich null, dann wäre damit auch automatisch sein Impuls gleich null – und somit exakt bestimmt. Da wir aber wissen, dass sich das Quantenobjekt innerhalb der Wände befindet, ist die maximale Ortsunschärfe \(\Delta x=L\). Damit wäre das Produkt \(\Delta x\cdot \Delta p_x\) gleich null und die Unschärferelation verletzt.
Beachte, dass die Nullpunktsenergie (wie auch die Energien für höhere Quantenzahlen) von dem Wandabstand \(L\) abhängen. Je kleiner der zur Verfügung stehende Raum, desto größer ist die Nullpunktsenergie!
17.5.8 Bestimmung der Wahrscheinlichkeitsamplitude
Die Amplitude \(A\) (siehe Wellenfunktionen für ein Kastenpotenzial) ist nach wie vor unbestimmt. Jetzt kommt die Normbedingung ins Spiel. Damit sich die Wellenfunktion für eine Wahrscheinlichkeitsinterpretation eignet, muss die Amplitude \(A\) so gewählt werden, dass:
\[ \int_{- \infty}^{+\infty} \psi^2\,\mathrm dx = 1 \]
Außerhalb der Box ist die Wellenfunktion überall null, daher können wir den Integrationsbereich auf das Intervall \(0<x<L\) einschränken.
\[ \begin{aligned} \int_{0}^{L} A^2\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right)^2\,\mathrm dx = {} & 1 \\ A^2\cdot\int_{0}^{L} \sin\left(\frac{n\cdot \pi\cdot x}{L}\right)^2\,\mathrm dx = {} & 1 \\ \end{aligned} \]
Um das Integral zu lösen, verwenden wir eine besondere Eigenschaft der \(\sin^2\)-Funktion aus (Bild 17.51). Hier kannst du auf der rechten Seite sehen, dass die Kurve das orange Rechteck genau in zwei gleich große Flächen teilt. Liegt die Nullstelle bei \(x=1\) ist der Flächeninhalt unter der Kurve genau \(1/2\).
In unserem Fall beträgt die Entfernung bis zum Nullpunkt aber \(L\), daher liefert das Integral den \(L\)-fachen Wert, also \(L/2\), und damit ist:
\[ \begin{aligned} A^2\cdot\frac{L}{2}= {} & 1 &&\qquad\Bigr\rvert\cdot \frac{2}{L}\\ A^2= {} & \frac{2}{L} &&\qquad\Bigr\rvert\;\sqrt{(\ldots)}\\ \end{aligned} \]
Also
\[\begin{equation} A=\sqrt{\frac{2}{L}} \tag{17.26} \end{equation}\]
Damit lautet die vollständige Wellenfunktion für ein unendliches Kastenpotenzial der Breite \(L\):
\[\begin{equation} \psi(x) = \sqrt{\frac{2}{L}}\cdot\sin\left(\frac{n\cdot \pi\cdot x}{L}\right),\qquad n=1,2,3,\ldots \tag{17.27} \end{equation}\]
17.5.9 Wahrscheinlichkeitsdichte
Die Antreffwahrscheinlichkeit für ein Quantenobjekt innerhalb der Box ist durch die Wahrscheinlichkeitsdichte \(\psi^2(x)\) bestimmt. In Bild 17.52 siehst du diese Funktion für die ersten Quantenzahlen dargestellt. Im Vergleichsbild siehst du die gemessenen Orte im simulierten Experiment für eine Vielzahl an Quantenobjekten im gleichen Energiezustand.
Beachte, dass für niedrige Quantenzahlen die Wahrscheinlichkeit, ein Quantenobjekt anzutreffen, nicht für alle Stellen gleich groß ist. Ganz im Gegensatz zur klassischen Betrachtung, wo die Antreffwahrscheinlichkeit überall gleich groß ist (strichlierte Linie). Die Breite des grünen Streifens im Bild soll die Genauigkeit eines Messinstruments zeigen. Für hohe Quantenzahlen nimmt die Welligkeit immer mehr zu. Sinkt die Welligkeit unter die Genauigkeit des Messinstruments, wird die Antreffwahrscheinlichkeit im gesamten Intervall wieder gleich groß. Hier haben wir wieder ein Beispiel für das Korrespondenzprinzip, nachdem für große Quantenzahlen die quantenmechanische Beschreibung in die klassische Physik übergeht.
17.5.10 Teilchen in einem Kasten für 2D und 3D
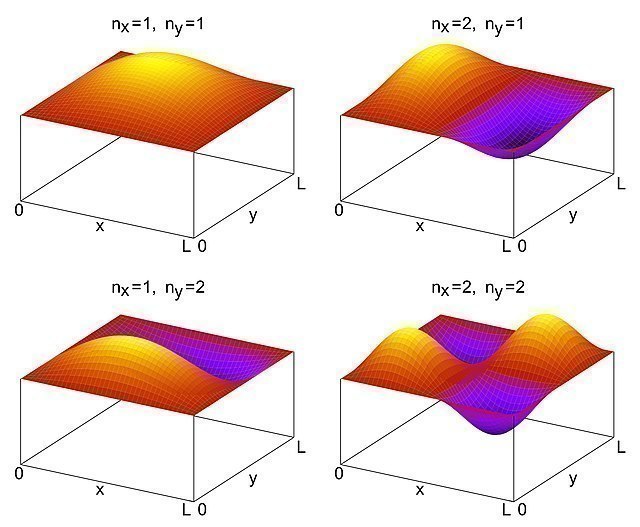
Die Verallgemeinerung für ein zwei und drei dimensionales unendliches Kastenpotenzial ist relativ einfach. Pro Achse kommt eine Quantenzahl dazu. Der Zustand eines Quantenobjekts wird dann durch zwei (2D) oder drei (3D) voneinander unabhängiger Quantenzahlen beschrieben. In Bild 17.53 siehst du die Wellenfunktionen \(\psi(x,y)\) für den zweidimensionalen Fall für die ersten Werte der Quantenzahlen \(n_x\) und \(n_y\).
In Bild 17.54 siehst du die Wahrscheinlichkeitsdichte \(\psi^2(x,y,z)\) für den dreidimensionalen Fall für die ersten Werte der Quantenzahlen \(n_x\), \(n_y\) und \(n_z\) dargestellt.