17.2 Teilchen mit Welleneigenschaften
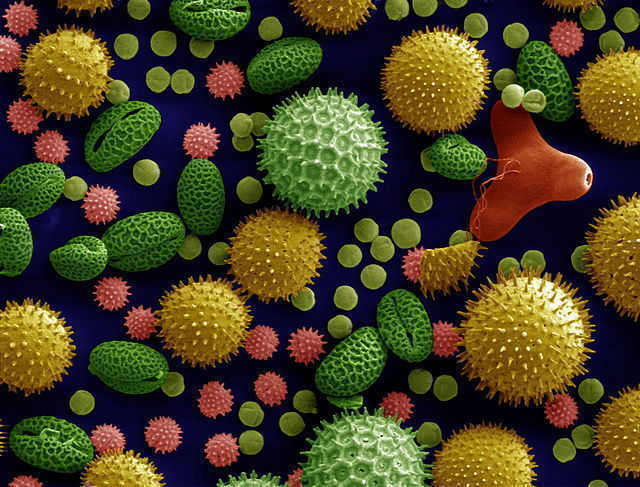
Die detailreiche Aufnahme in Bild 17.17 von Pollen wurde nicht mit einem Lichtmikroskop, sondern mit einem Elektronenmikroskop gemacht (und nachträglich eingefärbt).
Etwa zur selben Zeit, als bei Lichtwellen Teilcheneigenschaften festgestellt wurden, wurden Welleneigenschaften bei Elektronen und anderen Objekten entdeckt, die bis dahin für reine Teilchen gehalten wurden.
17.2.1 Materiewellen
In Bild 17.18 siehst du Louis de Broglie (ausgesprochen „de Broi“ Audio abspielen ). Er stellte in einer seiner Arbeiten 1923 eine gewagte Hypothese auf: Wenn Licht Teilcheneigenschaften zeigt, vielleicht besitzen Teilchen auch Welleneigenschaften.
Er nennt die mit einem Teilchen verknüpfte Welle Materiewelle (engl. matter wave). Setzt du den Teilchenimpuls \(p=m\cdot v\) und den Impuls eines Photons \(p=h/\lambda\) gleich, erhältst du den Ausdruck
| \[\begin{equation} \lambda=\frac{h}{m\cdot v} \tag{17.8} \end{equation}\] |
für die Größe der Wellenlänge der Materiewelle eines Teilchens (De-Broglie-Wellenlänge). In dieser Gleichung bedeuten:
- \(\lambda\), die Wellenlänge der Materiewelle (in \(\mathrm{m}\))
- \(h\), das Plancksche Wirkungsquantum (eine Konstante mit dem Wert \(6{,}6\cdot 10^{-34}\;\mathrm{Js}\))
- \(m\), die Masse des Teilchens (in \(\mathrm{kg}\))
- \(v\), die Geschwindigkeit des Teilchens (in \(\mathrm{m/s}\))
17.2.2 Davisson-Germer-Experiment
Wird ein Röntgenstrahl (Licht mit einer Wellenlänge im Nanometer-Bereich) auf einen Kristall gerichtet, wirken die einzelnen Kristall-Atome wie punktförmige Wellenerreger. Die regelmäßige Anordnung der Atome in einem Kristall-Gitter bewirkt ein winkelabhängiges Interferenzmuster. Aus dem Winkel zwischen einfallendem Strahl und Interferenzmaximum kann der Abstand der Gitterebenen berechnet werden. Für einen Nickelkristall ist dieser Abstand \(d=91\;\mathrm{pm}\) (Picometer oder \(10^{−12}\;\mathrm{m}\)).
Im Davisson-Germer-Experiment richteten 1927 Clinton Davisson und Lester Germer (Bild 17.19) statt eines Röntgenstrahls einen Strahl aus Elektronen auf einen Nickelkristall. Dabei wählten sie die Beschleunigungsspannung der Elektronenkanone so, dass die De-Broglie-Wellenlänge ((17.8) in der Größenordnung von Röntgenstrahlen war. Die Elektronen wurden nicht einfach nur zufällig gestreut, sondern verhielten sich wie Röntgenstrahlung und zeigten im selben Winkel ein ausgeprägtes Interferenzmaximum. Mit diesem Experiment wurde sowohl die Materiewellen-Hypothese als auch die Formel für die De-Broglie-Wellenlänge bestätigt (Nobelpreis 1937).
17.2.3 Elektronenbeugungsröhre
Bei einem ähnlichen Experiment, der Elektronenbeugungsröhre (engl. electron diffraction tube), zeigt sich ein Beugungsbild bei der Streuung eines Elektronenstrahls an einer Graphitfolie (Bild 17.20).
Den Versuchsaufbau siehst du in Bild 17.21. In einem evakuierten Glaskolben werden mithilfe einer Glühkathode freie Elektronen erzeugt, die anschließend mit einer Anodenspannung von \(5\;\mathrm{kV}\) beschleunigt werden. Die Anode besteht aus einer dünnen Graphitfolie, die der Elektronenstrahl passiert. Auf dem Leuchtschirm dahinter entsteht ein heller Fleck, der von Kreisringen umgeben ist.
17.2.4 Elektron als stehende Welle
Die Annahme, dass ein Teilchen auch eine Wellenlänge besitzt (De-Broglie-Wellenlänge), lieferte zum ersten Mal eine vage Idee, warum nur bestimmte Bahnen für Elektronen in einem Atom erlaubt sein sollen: Nur wenn die Wellenlänge auf einer Bahn durch konstruktive Interferenz zu einer stehenden Welle führt, handelt es sich um eine „erlaubte“ Bahn (Bild 17.22, \(r_2\)). Auf allen anderen Bahnen kann sich keine zeitlich stabile, stehende Welle ausbilden.
Konstruktive Interferenz erhalten wir genau dann, wenn der Umfang \(U=2\cdot \pi\cdot r\) der kreisförmigen Bahn ein Vielfaches der Wellenlänge \(n\cdot \lambda\) ist.
\[ \begin{aligned} 2\cdot \pi\cdot r = {} & n\cdot \lambda &&\qquad\Bigr\rvert\qquad\lambda=\frac{h}{m\cdot v} \\ 2\cdot \pi\cdot r = {} & n\cdot \frac{h}{m\cdot v} &&\qquad\Bigr\rvert\cdot \frac{m\cdot v}{2\cdot \pi}\\ m\cdot v\cdot r = {} & n\cdot \frac{h}{2\cdot \pi} &&\qquad\Bigr\rvert\qquad L=m\cdot v\cdot r \\ L = {} & n\cdot \frac{h}{2\cdot \pi} \\ \end{aligned} \]
Das ist genau die Bedingung für den Drehimpuls der „erlaubten“ Bahnen im Bohrschen Atommodell.
17.2.5 Rasterelektronenmikroskop
Herkömmliche Lichtmikroskope können keine Objekte auflösen, die kleiner sind als die Wellenlänge des sichtbaren Lichts. Beim Rasterelektronenmikroskop (engl. scanning electron microscope (SEM)) wird daher anstelle von Licht ein Strahl aus Elektronen verwendet. Die De-Broglie-Wellenlänge kann durch eine Beschleunigungsspannung verändert werden, wodurch eine noch höhere Auflösung von bis zu 150.000-fach erreicht wird.
In Bild 17.23 siehst du das vereinfachte Funktionsprinzip eines Rasterelektronenmikroskops. Für die Fokussierung des Elektronenstrahls wird statt optischer Linsen das Feld von Magnetspulen verwendet. Die Probe wird mit dem Elektronenstrahl zeilenweise abgetastet und das Ergebnis auf dem Monitor dargestellt. Um Wechselwirkungen mit Luft-Molekülen zu vermeiden, befindet sich die Probe im Vakuum. Während der Abtastung der Probe wird zusätzlich punktweise eine Spektralanalyse durchgeführt. Dabei regt der Abtaststrahl die Hüllenelektronen der Atome der Probe an. Die anschließend ausgesandte elektromagnetische Strahlung gibt Auskunft über die jeweilige Atomsorte.
Ein Elektronenmikroskop liefert nur Intensitätsunterschiede, daher ein Graustufenbild. Die Aufnahme in Bild 17.17 wurde nachträglich eingefärbt.