17.7 Quantenmechanisches Atommodell
In Bild 17.64 siehst du das klassische Modell eines Atoms.
Diese Vorstellung ist zwar sehr anschaulich, aber sehr weit von der aktuellen Sichtweise entfernt. In diesem Kapitel erfährst du, wie die Physik aktuell die Elektronenhülle eines Atoms versteht (Quantenmechanisches Atommodell).
17.7.1 Probleme des klassischen Atommodells
Im klassischen Atommodell wurde versucht, alle Phänomene auf das mechanische Verhalten von Elektronen (zum Beispiel ihrem Bahndrehimpuls) zurückzuführen. Dies erwies sich aber als „Sackgasse“, da sich viele Phänomene damit nicht beschreiben lassen. Hier sind einige davon:
Linienspektren zeigen, dass die Elektronen bei allen Atomen desselben Elements dieselben „Bahnen“ einnehmen. Bei Planeten sind hingegen beliebige Bahnradien möglich. Das Elektron als stehende Welle zu erklären, ist ein verzweifelter Versuch, das Verhalten mithilfe der klassischen Physik zu erklären. Es lässt jedoch viele Fragen offen. Eigentlich gibt es nach der klassischen Physik keinen Grund für die Einschränkung!
Beschleunigte Elektronen strahlen Energie in Form von elektromagnetischen Wellen ab. Jede Kreisbewegung ist eine beschleunigte Bewegung. Daher müssten Elektronen auf ihrer Bahn um das Atom ständig Energie verlieren. Dadurch würde ihr Bahnradius ständig abnehmen und jedes Elektron müsste in kürzester Zeit in den Kern stürzen. Es kann eigentlich keine stabilen Atome geben.
Das quantenmechanische Atommodell kann das alles erklären.
17.7.2 Quantenzahlen für gebundene Elektronen
Nach dem quantenmechanischen Atommodell haben Elektronen nämlich keine klassische Bahn um einen Atomkern, sondern nur Aufenthaltswahrscheinlichkeiten. Für die Beschreibung der Lösungen für die Wellenfunktion \(\psi(x,y,z)\) für ein Elektron in einem dreidimensionalen Atomkern-Potenzial sind (im Gegensatz zum unendlichen Kastenpotenzial) sogar vier (zum Teil voneinander abhängige!) Quantenzahlen notwendig. Zu jeder Kombination dieser Quantenzahlen gehört ein eindeutiger diskreter Energiewert.
\[\begin{equation} \begin{aligned} n & = 1,2,3,\ldots && (\text{Hauptquantenzahl})\\ l & = 0,1,2,\ldots,(n-1) && (\text{Drehimpulsquantenzahl})\\ m_l & = 0, \pm 1,\pm 2,\ldots,\pm \ell && (\text{Magnetische Bahnquantenzahl})\\ m_s & = +\frac{1}{2}, -\frac{1}{2} && (\text{Spin-Quantenzahl})\\ \end{aligned} \tag{17.29} \end{equation}\]
Die Hauptquantenzahl entspricht im klassischen Atommodell der Schalen-Nummer, die du bereits kennengelernt hast.
Um beobachtbare Phänomene wie zum Beispiel den Diamagnetismus zu erklären, wurden im klassischen Atommodell den einzelnen Elektronen einer Schale unterschiedliche elliptische Bahnen um den Atomkern zugeordnet. Die Drehimpulsquantenzahl gemeinsam mit der magnetischen Bahnquantenzahl beschreiben das magnetische Dipolmoment eines Elektrons, das sich nach dem klassischen Modell durch die umlaufende Bewegung der Elektronen um den Atomkern ergeben soll.
Um Phänomene wie den Paramagnetismus erklären zu können, wurden im klassischen Atommodell unabhängig von ihrer Schale und ihrer Bahn den Elektronen ein Eigendrehimpuls (Spin) zugeschrieben. Die Spin-Quantenzahl beschreibt das magnetische Dipolmoment, das nach dem klassischen Modell durch den Eigendrehimpuls der Elektronen zustande kommt.
17.7.3 Orbitale
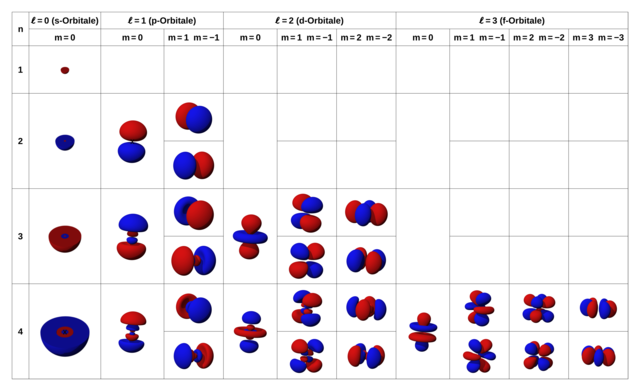
Die wahrscheinlichsten Antrefforte für Elektronen eines bestimmten Energiezustandes um einen Atomkern werden Orbitale (engl. orbitals) genannt. Die Wahrscheinlichkeitswolken werden oft als „Ballons“ dargestellt (Bild 17.66). Das Volumen zeigt den Bereich, innerhalb dessen \(90\,\%\) aller Elektronen einer bestimmten Energie angetroffen werden (Bild 17.65). In roten Bereichen ist die Wellenfunktion positiv, während sie in blauen Bereichen negativ ist.
Jedem Orbital entspricht ein Satz der vier Quantenzahlen für Elektronen. In Bild 17.66 siehst du möglichen Orbitale des Wasserstoffatoms für die ersten paar Quantenzahlen im Überblick. Durch die Spin-Quantenzahl kann jedes dieser Orbitale von zwei Elektronen besetzt werden.
Du bist vielleicht erstaunt, dass die Form der Orbitale teils stark von einer Kugelgestalt abweicht. Aber bedenke, dass jede Lösung der Schrödingergleichung einer stehenden Welle im Raum entsprechen muss. Je nach der Form werden sie s-Oribtale (kugelförmig), p-Orbitale (hantelförmig), usw. genannt.
Links:
- Nachschlagen: Wasserstoff Orbitale in 3D bis zur Hauptquantenzahl 7
17.7.4 Besetzungsregel
Jede Hauptquantenzahl entspricht einer Schale im klassischen Atommodell:
- \(n=1\) entspricht der K-Schale
- \(n=2\) entspricht der L-Schale
- \(n=3\) entspricht der M-Schale
- \(n=4\) entspricht der N-Schale
- …
Die Orbitale werden von den Elektronen stets so besetzt, dass ein Elektron immer den ersten freien Platz mit der niedrigsten Energie besetzt. Teilweise besitzen aber Orbitale aus höheren Schalen eine niedrigere Energie (Bild 17.67). Daher wird nicht immer eine Schale voll besetzt, bevor die nächste begonnen wird.
Als Merkhilfe für die Besetzungsreihenfolge kannst du den Raster in Bild 17.68 verwenden.
Das Element Kalium hat 19 Elektronen. Wenden wir die Besetzungsregel an, erhalten wir:
Zunächst wird die erste Schale mit 2 Elektronen (1s-Orbital) und dann die zweite Schale mit 8 Elektronen besetzt (2 im 2s-Orbital und 6 in den 2p-Orbitalen). Verbleiben noch \(19-2-2-6=9\) Elektronen.
Es folgen das 3s (2 Elektronen) und die 3p Orbitale (6 Elektronen). Verbleibt noch \(9-2-6=1\) Elektron.
Das 4s Orbital (2 Elektronen) besitzt aber eine niedrigere Energie als das 3d Orbital (10 Elektronen). Das letzte Elektron ist im Orbital 4p untergebracht.
Als Elektronenkonfiguration erhältst du: \(1\mathrm{s}^22\mathrm{s}^22\mathrm{p}^63\mathrm{s}^23\mathrm{p}^64\mathrm{s}^1\). Die Hochzahl hinter dem Orbital gibt dabei die Anzahl der Elektronen in diesem Orbital an.
Links:
- Nachschlagen: Elektronenkonfigurationen aller Elemente
17.7.5 Hundsche Regel
Durch die Elektron-Elektron-Wechselwirkung innerhalb eines Orbitals werden selbst Orbitale gleicher Energie immer zuerst einfach, dann erst doppelt besetzt. Dieses Verhalten wird Hundsche Regel (engl. Hund’s rule, nach Friedrich Hund) genannt.
In Bild 17.69 siehst du ein Beispiel für diese Regel. Sauerstoff besitzt acht Elektronen. Die ersten vier Elektronen belegen die Orbitale \(1\mathrm{s}\) und \(2\mathrm{s}\). Alle drei \(2\mathrm{p}\) Orbitale besitzen die gleiche Energie. Nach der Hundschen Regel müssen alle Orbitale zunächst einfach besetzt werden, bevor ein Orbital doppelt besetzt wird. Die Pfeile im Diagramm zeigen die Spin-Quantenzahl \(1\) (up) oder \(-1\) (down) der Elektronen an.
17.7.6 Orbitale und das Periodensystem
Die Orbitale spiegeln sich auch im Aufbau des Periodensystems wider. In Bild 17.70 siehst du das äußerte Orbital für jedes Element, in dem sich noch ein Elektron befindet.
17.7.7 Ausschließungsprinzip
Die Natur folgt immer dem Prinzip der niedrigsten Energie. Warum befinden sich dann nicht alle Elektronen im 1s-Orbital?
Elektronen können es einfach nicht – es wurde noch nie in der Natur festgestellt. Diese Unmöglichkeit hat Wolfgang Pauli in seinem Ausschließungsprinzip (engl. Pauli exclusion principle) – ihm zu Ehren auch als Pauli-Verbot bezeichnet – formuliert.
| Zwei Elektronen eines Atoms dürfen nicht in allen Quantenzahlen übereinstimmen. |
Das Pauli-Verbot gilt nicht nur für Elektronen, sondern auch für andere Quantenobjekte wie zum Beispiel für Protonen und Neutronen. Diese Quantenobjekte heißen Fermionen.
Es gibt aber auch Quantenobjekte wie zum Beispiel das Photon (Lichtteilchen) für die das Pauli-Verbot nicht gilt. Diese Quantenobjekte werden Bosonen genannt. Bosonen können alle dieselben Werte für die Quantenzahlen besitzen.
17.7.8 Chemische Bindungen aus quantenmechanischer Sicht
Atomorbitale hast du jetzt schon kennengelernt. Befinden sich zwei Atome so nahe, dass ihre Orbitale einander überlappen, entstehen durch Superposition neue, gemeinsame Orbitale – Molekülorbitale.
Wir zeigen die Entstehung von Molekülorbitalen am Beispiel von zwei Wasserstoff-Atomen \(\mathrm{H_a}\) und \(\mathrm{H_b}\). Jedes der beiden Atome besitzt ein Elektron in einem \(\mathrm{s1}\)-Orbital. Wenn der Ort des Elektrons des ersten Atoms durch die Wellenfunktionen \(\psi_a(\mathrm{s1})\) beschrieben wird und der des Elektrons des zweiten Atoms durch \(\psi_b(\mathrm{s1})\), ergeben sich durch Superposition die folgenden zwei möglichen Kombinationen:
- \(\psi_+ = \psi_a(\mathrm{s1})+\psi_b(\mathrm{s1})\) („bindend“) und
- \(\psi_- = \psi_a(\mathrm{s1})-\psi_b(\mathrm{s1})\) („anti-bindend“)
Die daraus resultierenden Wellenfunktionen siehst du in Bild 17.71.
In Bild 17.72 siehst du die Antreffwahrscheinlichkeitswolken, die aus den beiden Überlagerungen resultieren. Während bei dem bindenden Molekülorbital (a) für beide Elektronen die Antreffwahrscheinlichkeit in der Mitte am größten ist, befinden sich im anti-bindenden Molekülorbital (b) die Antreffwahrscheinlichkeiten für jedes der beiden Elektronen sogar jenseits des eigenen Atomkerns. Jedes dieser beiden Molekülorbitale kann zwei Elektronen aufnehmen.
Welche der Molekülorbitale werden von den beiden Elektronen besetzt? Die Antwort auf diese Frage liefert das Energiediagramm für die beiden Molekülorbitale (Bild 17.73). Links und rechts von der Mitte siehst du die \(\mathrm{s1}\)-Atomorbitale der getrennten Wasserstoff-Atome, die je mit einem Elektron besetzt sind. In der Mitte siehst du die gemeinsamen Molekülorbitale – unten das bindende und oben das anti-bindende Orbital. Warum das bindende Orbital eine geringere Energie besitzt, erklärt sich aus der Nullpunktsenergie. In diesem Orbital haben die Elektronen einen sehr viel größeren Aufenthaltsbereich als in ihren \(\mathrm{s1}\)-Atomorbitalen. Umgekehrt ist der Aufenthaltsbereich im anti-bindenden Orbital für jedes der beiden Elektronen sogar kleiner als in ihren Atomorbitalen, ihre Nullpunktsenergie ist daher größer.
Die Natur bevorzugt immer den Zustand kleinster Energie, daher befinden sich im Wasserstoff-Molekül beide Elektronen im energetisch tieferen, also im bindenden Orbital. Beachte, dass das Ausschließungsprinzip auch für Molekülorbitale gilt. Die beiden Elektronen müssen sich im gleichen Orbital zumindest durch ihren Spin unterscheiden.
Im Gegensatz zu Wasserstoff-Atomen besitzen Helium-Atome jeweils zwei Elektronen in ihren \(\mathrm{s1}\)-Orbitalen. Daraus ergibt sich die Besetzung der Molekülorbitale für zwei Helium-Atome wie in Bild 17.74. Nachdem das bindende Molekülorbital mit zwei Elektronen schon voll besetzt ist, müssen sich die zwei restlichen Elektronen im anti-bindenden Orbital befinden. Die Wirkungen bindend-antibindend heben einander aber auf und es kommt zu keiner Bindung der beiden Atome. Es kann keine \(\mathrm{He_2}\)-Moleküle geben.
