17.9 Standardmodell der Elementarteilchenphysik
Im Abschnitt über Atome hast du schon einiges über Protonen, Neutronen und Elektronen erfahren. Im Abschnitt Beta-Zerfall hast du von Positronen erfahren und auch Lichtteilchen (Photonen) kennst du schon.
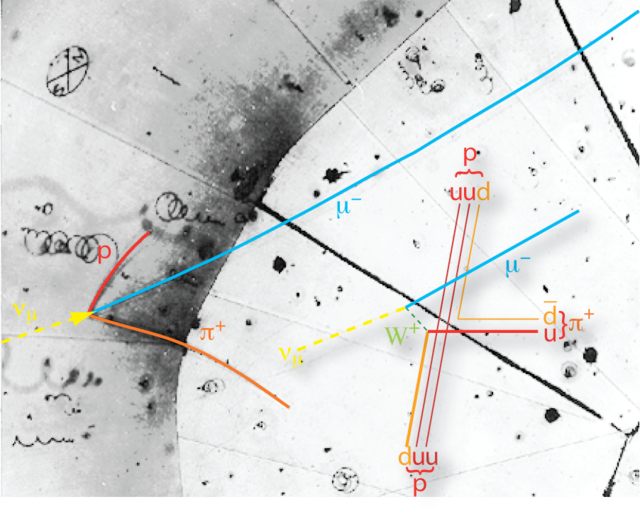
Bild 17.85: Spuren von Teilchen in einer Blasenkammer mit Anmerkungen (Originalaufnahme)
Anfang des 20. Jahrhunderts wurden in der kosmischen Strahlung mithilfe von Blasenkammer-Aufnahmen wie der in Bild 17.85 Spuren von bis dahin unbekannten „Teilchen“ gefunden. Ab den 1940er-Jahren wurden Protonen und Elektronen in Beschleuniger-Experimenten mit immer größeren Geschwindigkeiten gegen Atome oder auch gegeneinander geschossen und noch viel mehr unbekannte Teilchen kamen zum Vorschein.
In diesem Kapitel erfährst du von diesen Teilchen, in welche Gruppen sie sich einteilen lassen und welche von ihnen – nach unserem heutigen Erkenntnisstand – tatsächlich elementar sind und damit die wirklichen Bausteine des Universums sind.
Links:
- Website: A Particle Physics Course for High-School Students (englisch)
17.9.1 Hochenergiephysik
In den vorangegangenen Kapiteln haben wir uns angesehen, wie sich Quantenobjekte bei extrem kleinen Energien (Temperaturen) und in sehr kleinen Mengen verhalten. Die Quantenmechanik ließe sich auch als „Teilchenphysik bei niedriger Energie“ bezeichnen.

Bild 17.86: Ein Abschnitt der LHC Synchrotrons. Der blau Lack schützt die Magnete vor Rost.
Im Gegensatz dazu werden wir uns jetzt mit Quantenobjekten bei extrem hohen kinetischen Energien – wie sie üblicherweise nur in Teilchenbeschleunigern und in der kosmischen Strahlung vorkommt – beschäftigen (Bild 17.86). Dieser Bereich der Quantenphysik wird daher als Hochenergiephysik (engl. high-energy physics) bezeichnet. Da bei großen Energien vor allem der Teilchenaspekt der Quantenobjekte eine Rolle spielt, wird dieser Bereich auch als Teilchenphysik (engl. particle physics) bezeichnet.
17.9.2 Was ist ein Teilchen?
Das klingt nach einer ganz harmlosen Frage. Aber Physikerinnen und Physiker können weder sagen, was ein Teilchen genau „ist“ noch wie es „aussieht“ oder welche „Form“ es hat. Im Mikrokosmos können wir uns nur auf die Eigenschaften stützen, die uns unsere Messgeräte über diese Teilchen verraten, wie etwa die Masse, die wir bei einer Kollision aufgrund der Impulserhaltung feststellen können. Ein wenig ist unsere Situation vergleichbar mit der eines Spurenlesers (Bild 17.87). Obwohl wir die Teilchen niemals sehen können, versuchen wir aufgrund der Spuren, die sie im Detektor hinterlassen, sie zu unterscheiden und möglichst viele Eigenschaften davon abzuleiten.
Nur eines wissen wir mit Sicherheit: Bei Elementarteilchen handelt es sich nicht um Kugeln, wie wir sie aus dem Alltag kennen, auch wenn sie in vielen Abbildungen so dargestellt werden.
17.9.3 Blasenkammer
Eine relativ einfache Vorrichtung, um die Spuren von Teilchen sichtbar zu machen, ist die Blasenkammer (engl. bubble chamber). In einer Kammer (Bild 17.88, 1) befindet sich eine klare, durchsichtige Flüssigkeit (häufig flüssiger Wasserstoff). Kurz vor dem Experiment wird der Druck in der Kammer stark verringert (2). Die Temperatur der Flüssigkeit befindet sich jetzt oberhalb des Siedepunktes. Es fehlen allerdings die Siedekeime, daher siedet sie noch nicht (Siedeverzug, überkritische Flüssigkeit). Dringen Teilchen – zum Beispiel von einem Teilchenbeschleuniger kommend – in die Kammer ein, ionisieren sie die Wasserstoffatome entlang ihrer Bahn und werden dabei abgebremst. Die Ionen entlang der Teilchenbahn dienen jetzt als Keime für die Bildung von Gasblasen (Siedekeime) und ihre Spuren werden sichtbar (3).
Zusätzlich durchdringt die Kammer ein Magnetfeld (4). Während elektrisch geladene Teilchen aufgrund der Lorentzkraft abgelenkt werden und eine Spiralbahn hinterlassen, besitzen elektrisch neutrale Teilchen eine gerade Bahn. Die Größe der Spiralbahn lässt Rückschlüsse auf das Verhältnis \(Q/m\) (Ladung zu Masse) des Teilchens zu und der Umlaufsinn verrät das Vorzeichen der Ladung. Hat das Magnetfeld die Richtung wie in Bild 17.88 gezeigt (in die Bildebene hinein), bewegen sich positiv geladene Teilchen auf eine Bahn gegen den Uhrzeigersinn (Krümmung nach links) und umgekehrt.
Ganz ähnlich funktioniert die Nebelkammer. Statt einer Flüssigkeit befindet sich übersättigter Dampf in der Kammer. Die Ionen entlang der Teilchenbahn dienen als Kondensationskeime und die Spuren werden als Kondensstreifen sichtbar.
17.9.4 Spin
Elektronen verhalten sich so, als ob sie sich um ihre eigene Achse drehen. Im Experiment zeigen sie ein Verhalten wie bei einem fixen Drehimpuls der Größe:
\[\begin{equation} \frac{1}{2}\cdot\frac{h}{2\pi} \tag{17.36} \end{equation}\]
Diese Eigenschaft wird Spin genannt. Diese Eigenschaft ist unveränderlich, auch wenn sich das Elektron außerhalb eines Atoms befindet. Außerdem ist sie unabhängig von einer eventuellen (linearen) Geschwindigkeit des Elektrons.
Aus der Spin-Eigenschaft folgt, dass sich ein Elektron – analog einer geladenen rotierenden Kugel – wie ein kleiner magnetischer Dipol verhält (Bild 17.89).
Der Spin ist aber kein klassischer Drehimpuls! Die Quantisierung in der quantenmechanischen Beschreibung gilt nicht nur für die Größe des Spins, sondern auch für seine Orientierung. Wenn zum Beispiel auf einen Elektronenstrahl ein schwaches Magnetfeld einwirkt, das nicht stark genug ist, um alle Spins zu zwingen, sich in die gleiche Richtung auszurichten, werden sich einige der Spins in Richtung des Magnetfeldes (parallel) anordnen und der Rest in genau der entgegengesetzten Richtung (antiparallel) – egal in welche Richtung das äußere Magnetfeld zeigt! Würden wir dasselbe Experiment mit „klassischen“ Mini-Stabmagneten durchführen, würden wir alle möglichen Richtungen relativ zum Feld zufällig verteilt finden.
Auch andere Teilchen haben eine Spin-Eigenschaft. Der Spin wird üblicherweise immer als Vielfaches der „Einheit“ \(h/2\pi\) angegeben. Der Spin des Elektrons wird daher als \(1/2\) angegeben. Ist \(s\) die Größe des Spins, gibt es insgesamt \(2\cdot s+1\) mögliche Ausrichtungen in einem äußeren Feld.
| Spin | Ausrichtungen |
|---|---|
| 1/2 | 2 |
| 1 | 3 |
| 3/2 | 4 |
| … | … |
17.9.5 Stern-Gerlach-Versuch
Die Quantisierung der Spin-Richtung wurde erstmals 1922 von Otto Stern und Walther Gerlach experimentell nachgewiesen (Stern-Gerlach-Versuch). Den Versuchsaufbau siehst du in Bild 17.90.
Ein Strahl aus (elektrisch neutralen) Silberatomen durchfliegt ein inhomogenes Magnetfeld im Vakuum und trifft auf einen Schirm dahinter auf. Das Magnetfeld teilt den Strahl in zwei getrennte Teilstrahlen auf. Ein neutrales Silberatom besitzt insgesamt 47 Elektronen. Bis auf das \(5s\) Elektron heben sich aber alle anderen magnetischen Momente auf, sodass sich das gesamte Atom magnetisch wie ein einziges Elektron mit Spin-1/2 verhält.
Warum muss das Magnetfeld inhomogen sein? In einem homogenen Feld ist die Kraft auf beide Pole immer gleich groß, daher wird ein Dipol nur gedreht. In dem inhomogenen Magnetfeld in Bild 17.90 ist die Kraft auf den Südpol des Dipols stärker und führt zu einer Ablenkung – je nach Ausrichtung des Spins – nach oben oder unten.
Links:
17.9.6 Elementarteilchen
Durch Beschleuniger-Experimente haben die Physikerinnen und Physiker im Laufe des 20. Jahrhunderts mehr als hundert unterschiedliche Teilchen gefunden – scherzhaft als „Teilchenzoo“ bezeichnet. Es stellte sich jedoch heraus, dass die meisten davon aus noch kleineren Bausteinen aufgebaut sind, also nicht elementar sind. Nach dem Standardmodell der Elementarteilchenphysik gibt es nur 17 tatsächliche Elementarteilchen (Bild 17.91).
Die Elementarteilchen lassen sich in folgende Gruppen einteilen:
Sechs Quarks: Diese Elementarteilchen sind nicht direkt beobachtbar! Sie kommen nur in Kombination mit anderen Quarks vor und bilden etwa das Proton oder das Neutron.
Sechs Leptonen: Kleine Elementarteilchen, die direkt beobachtbar sind. Den bekanntesten Vertreter der Gruppe kennst du schon, das Elektron.
Vier Eichbosonen oder Austauschteilchen: Diese Teilchen sind für die Übertragung von Kräften zwischen Teilchen verantwortlich. Der bekannteste Vertreter dieser Gruppe ist das Photon. Es ist für die Übertragung der elektrischen Kraft verantwortlich.
Das Higgs-Teilchen: das neueste Mitglied im Standardmodell. Das hinter dem Higgs-Teilchen stehende Higgs-Feld verleiht allen Teilchen ihre Masse.
In den folgenden Abschnitten und im nächsten Kapitel erfährst du mehr über das Standardmodell und seine Untergruppen.
17.9.7 Quarks
Murray Gell-Mann (Nobelpreis 1969) und andere verglichen die Eigenschaften der bisher bekannten Teilchen und konnte teilweise ein Ordnungsprinzip dahinter entdecken. Nach diesem Modell sind die meisten Teilchen einfach eine Kombination aus einigen wenigen Unterbausteinen – den sogenannten Quarks (gesprochen „Kworks“). Für den Zusammenhalt von Quarks ist die starke Wechselwirkung verantwortlich.
Quarks haben als einzige Teilchen keine ganzzahlige elektrische Ladung. Von den sechs Quarks im Standardmodell haben drei eine Ladung von \(+2/3e\) (Up-Quark \(\mathrm{u}\), Charm-Quark \(\mathrm{c}\) und Top-Quark \(\mathrm{t}\)) und drei \(-1/3e\) (Down-Quark \(\mathrm{d}\), Strange-Quark \(\mathrm{s}\) und Bottom-Quark \(\mathrm{b}\)). Die unterschiedlichen Quark-Arten werden auch als „Quark-Flavours“ (Geschmacksrichtung) bezeichnet.
Alle Quarks haben einen Spin von \(1/2\).
Beim Versuch, Teilchen, die aus Quarks bestehen (Hadronen) durch Beschuss mit Teilchen ausreichend großer Energie zu „zerschlagen“, binden sich die Quarks stets sofort zu neuen Hadronen. Einzelne freie Quarks konnten bisher nicht beobachtet werden. In der Natur lassen sich außerdem nur Teilchen mit einem ganzzahligen Vielfachen der Elementarladung messen. Die Bezeichnung „Elementar“ladung ist daher weiterhin zulässig.
17.9.8 Leptonen
Die Lepton (engl. lepton) im Standardmodell besteht aus einer Gruppe von Elementarteilchen, die keine Farbladung besitzen und damit nicht an der starken Wechselwirkung teilnehmen. Alle Leptonen haben einen Spin von \(1/2\) und sind damit Fermionen, die sich in einem gebundenen System durch mindestens eine Eigenschaft (Quantenzahl) voneinander unterscheiden müssen.
Die eine Hälfte der Leptonen besitzen eine elektrische Ladung (\(-1e\)): das Elektron (\(\mathrm{e}\)), das Myon (\(\mathrm{\mu}\)) und das Tauon (\(\mathrm{\tau}\)). Davon ist nur das Elektron stabil. Das Myon und das Tauon zerfallen nach kurzer Zeit in andere Teilchen. Alle geladenen Leptonen können mit anderen Teilchen Verbindungen eingehen.
Jedes geladene Lepton hat ein zugeordnetes ungeladenes Lepton, ein sogenanntes Neutrino (Verniedlichungsform von „Neutron“, neutrales Teilchen; bezeichnet mit dem griechischen Kleinbuchstaben Ny): Elektron-Neutrino (\(\mathrm{\nu_e}\)), Myon-Neutrino (\(\mathrm{\nu_\mu}\)) und Tauon-Neutrino (\(\mathrm{\nu_\tau}\)). Alle Neutrinos sind stabil. Im Gegensatz zu den geladenen Leptonen wechselwirken Neutrinos kaum mit Materie und sind äußerst schwierig nachzuweisen. Immerhin gehen fast alle Neutrinos von der Sonne sogar ungehindert durch die gesamte Erde hindurch!
Der Name leitet sich von dem griechischen Wort leptós für „dünn, schmal, klein“ ab. Es soll darauf hindeuten, dass es nicht aus weiteren Teilchen aufgebaut ist. Das bedeutet aber nicht, dass alle Leptonen „leicht“ sind: Das Tauon ist rund doppelt so schwer wie ein Proton!
17.9.9 Elektronenvolt pro c Quadrat
Nach der Masse-Energie-Äquivalenz entspricht die Energie eines Elektronenvolts einer bestimmten Masse. In der Teilchenphysik ist es üblich, die Masse als Vielfaches von \(1\;\mathrm{eV}/c^2\) auszudrücken, wobei \(c\) der Vakuumlichtgeschwindigkeit entspricht. Ein „Elektronenvolt pro c Quadrat“ (oder „eV durch c Quadrat“, engl. Electronvolt per c squared oder eV over c squared) in Kilogramm ausgedrückt lautet:
\[ 1\;{\text{eV}}/c^{2}={\frac {(1{,}602\ 176\ 634\cdot 10^{-19}\,{\text{C}})\cdot 1\,{\text{V}}}{(299\ 792\ 458\;\mathrm {m/s} )^{2}}}=1{,}782\ 661\ 92\cdot 10^{-36}\;{\text{kg}} \]
Da sich in der Hochenergiephysik ständig Teilchen umwandeln, Bindungsenergie frei wird oder als Masse in gebundenen Systemen gespeichert wird, hat diese Einheit praktische Vorteile. Zum Beispiel besitzen sowohl das Elektron als auch das Positron eine Masse von \(0{,}511\;\mathrm{MeV}/c^2\). Treffen beide Teilchen zusammen, kommt es zur Annihilation und die dabei freigesetzte Energie ist einfach:
\[ 2\cdot 0{,}511\;\mathrm{MeV} = 1{,}022\;\mathrm{MeV} \]
17.9.10 Generationen und Symmetrien
Das Standardmodell weist einige erstaunliche Symmetrien auf. Zunächst lassen sich die Fermionen in drei Spalten einteilen, die Familien oder Generationen genannt werden (Bild 17.92). Die erste Spalte besteht aus den Elementarteilchen der 1. Generation. Hier befinden sich die Elementarteilchen, aus denen unsere alltägliche Materie besteht. Das up- und down-Quark sind die Bestandteile von Proton und Neutron und ergeben mit dem Elektron die Bausteine aller Atome.
Zu jedem Elementarteilchen gibt es in der nächsten Generation ein entsprechend massereicheres Teilchen als in der Vorgängergeneration (in Bild 17.92 ist für jedes Teilchen die Masse in der äquivalenten Ruheenergie in der Einheit Elektronenvolt angegeben). Generell gilt: je massereicher, desto kurzlebiger ein Teilchen. Die Halbwertszeit nimmt also mit jeder Generation ab.
In jeder Generation gibt es genau zwei Quarks und zwei Leptonen. In jeder Generation gibt es genau ein elektrisch geladenes und ein ungeladenes Lepton (Neutrino). Als neben dem up- und down-Quark ein drittes Quark gefunden wurde, fanden die Physikerinnen und Physiker das „strange“ (seltsam). Als dann aber ein weiteres gefunden wurde und sich die Symmetrie in der 2. Generation abzeichnete, fanden sie das einfach nur „charming“ (zauberhaft).
Momentan gibt es keine experimentellen Befunde, die darauf hindeuten, dass es eine vierte, fünfte oder sogar höhere Generationen geben könnte. Warum es allerdings genau drei Generationen gibt, gehört zu den großen ungelösten Fragen der Physik.
17.9.11 Antimaterie
Der Überblick aller Elementarteilchen in Bild 17.91 ist im wahrsten Sinne des Wortes nur die „halbe Wahrheit“. Denn nach dem Standardmodell gibt es für jedes Teilchen – bis auf die Eichbosonen – ein Gegenstück, ein sogenanntes Antiteilchen (engl. antiparticle). Teilchen und Antiteilchen besitzen dabei identischen Eigenschaften, aber mit entgegengesetzten physikalischen Ladungen. Das Antiteilchen eines up-Quarks (\(\mathrm{u}\)) mit der elektrischen Ladung \(+2/3\) und grüner Farbladung wäre dann das Anti-Up-Quark (\(\overline{\mathrm{u}}\)) mit der elektrischen Ladung \(-2/3\) und der antigrüner (magentafarbenen) Farbladung.
Damit ist ein Neutron – obwohl es keine elektrische Ladung besitzt – nicht sein eigenes Antiteilchen. Während ein Neutron (\(\mathrm{n}\)) aus einem up-Quark und zwei down-Quarks besteht (\(\mathrm{udd}\)), enthält ein Antineutron (\(\overline{\mathrm{n}}\)) ein Anti-up-Quark und zwei Anti-down-Quarks (\(\overline{\mathrm{u}}\overline{\mathrm{d}}\overline{\mathrm{d}}\)). Damit unterscheidet sich ein Neutron von einem Anitneutron auch durch weitere Eigenschaften, wie etwa der Baryonenzahl: \(+1\) für ein Neutron und \(-1\) für ein Antineutron.
Wie du gesehen hast, werden Antiteilchen üblicherweise mit einem Querstrich gekennzeichnet. Die Ausnahme bilden Leptonen mit elektrischer Ladung, die meist durch ein hochgestelltes Vorzeichen dargestellt werden. Das Antiteilchen des negativ geladenen Elektrons (\(\mathrm{e}^-\)) ist das positiv geladene Positron (\(\mathrm{e}^+\)).
Neutrinos besitzen weder eine Farbladung noch elektrische Ladung. Neutrinos und Antineutrinos unterscheiden sich nur durch ihre Leptonenzahl, die für alle Leptonen \(+1\) und ihre Antiteilchen \(-1\) ist.
In Bild 17.93 siehst du alle Elementarteilchen und ihre Antiteilchen.
Alle physikalischen Gesetze gelten ebenso für Antiteilchen (Ladungsinvariant). Antiprotonen, Antineutronen und Antielektronen (Positronen) sind die Bausteine für Antimaterie (engl. antimatter). Ein ganzes Universum aus Antimaterie („Antiwelt“) würde exakt gleich wie unser Universum aus Materie funktionieren.
Trifft allerdings ein Teilchen auf sein Antiteilchen, kommt es zur Paarvernichtung (Annihilation) und die gesamte Masse und Energie der Teilchen wird in Strahlung umgewandelt. Daher können Materie und Antimaterie nicht nebeneinander existieren. In der Antimatter Factory am CERN wird Antimaterie in geringsten Mengen hergestellt, um damit zu experimentieren. In einer sogenannten Paul-Falle (Quadrupolfalle) wird die Antimaterie in einem elektromagnetischen Wechselfeld in Schwebe gehalten und von Materie so lange wie möglich getrennt.
Warum wir trotz der Symmetrie von Materie und Antimaterie im beobachtbaren Universum fast ausschließlich Materie vorfinden (Baryonenasymmetrie), gehört ebenfalls zu den großen ungelösten Fragen der Physik.
17.9.12 Farbladung
Um zu beschreiben, welche Kombinationen von Quarks auftreten können, wurde die Eigenschaft der Farbladung oder (engl. color charge) eingeführt (Bild 17.94).
Der Name kommt von der Eigenschaft der additiven Farbmischung, bei der sowohl die Summe alle drei Primärfarben (Rot, Grün, Blau) als auch die Summe von Farbe und Komplementärfarbe (zum Beispiel Blau und Antiblau (Gelb)) eine unbunte Farbe ergeben – hier als „farblos“ bezeichnet. Diese Farbbezeichnungen haben nichts mit der alltäglichen Bedeutung von „Farbe“ im optischen Sinne zu tun und ist lediglich eine praktische Analogie.
Zusätzlich zu allen anderen Eigenschaften (Ladung, Spin,…) hat jedes Quark noch eine Farbladung. Dabei gilt:
- Jedes der sechs Quarks besitzt eine von drei Farbladungen rot, grün oder blau (18 Kombinationen)
- Jedes der sechs Antiquarks besitzt eine von drei Anti-Farben antirot (Türkis oder Cyan), antigrün (Purpurrot, Magenta) oder antiblau (Gelb) besitzen (ebenfalls 18 Kombinationen)
Alle Hadronen (Kombinationen aus Quarks) haben keine Farbladung mehr – die Kombination der Farbladungen ihrer Quarks ergibt immer „farblos“.
17.9.13 Hadronen
Alle Teilchen, die aus zwei oder mehr Quarks aufgebaut sind, werden als Hadronen (engl. hadrons) bezeichnet. Ihr Name leitet sich vom griechischen Wort hadrós für „dick‚ stark“ ab. Sie werden von der starken Wechselwirkung zusammengehalten.
Da jedes Quark einen Spin von \(1/2\) besitzt, werden bei Hadronen prinzipiell zwei Gruppen unterschieden:
Mesonen, sie bestehen aus zwei Quarks, haben ganzzahligen Spin und sind damit Bosonen.
Baryonen, sie bestehen aus drei Quarks, haben halbzahligen Spin und sind damit Fermionen.
Daneben gibt es noch sogenannte exotische Hadronen, die aus mehr als drei Quarks bestehen, wie zum Beispiel Tetraquarks und Pentaquarks.
17.9.14 Mesonen
Als Meson werden Teilchen bezeichnet, die jeweils aus zwei Quarks bestehen – einem Quark und einem Antiquark. Da jedes Quark einen Spin von \(1/2\) besitzt, haben alle Mesonen einen ganzzahligen Spin und sind damit Bosonen. Der Name leitet sich vom griechischen tó méson „das Mittlere“ ab. Alle Mesonen sind instabil!
In Bild 17.95 siehst du als Beispiel für ein Meson ein Pion. Es besteht aus einem Up-Quark (Ladung \(+2/3e\)) und einem Down-Antiquark (Ladung \(-(-1/3e)=+1/3e\)). Es hat daher eine Gesamtladung von \(+2/3e+1/3e=+e\) und ist damit positiv geladen.
17.9.15 Baryonen
Baryonen (engl. baryon) bestehen aus jeweils drei Quarks (oder als Antibaryonen aus jeweils drei Antiquarks). Alle Baryonen haben halbzahligen Spin und sind damit Fermionen – unterliegen also dem Paulischen Ausschließungsprinzip. Der Name leitet sich aus dem altgriechischen Wort barýs für „schwer“ oder „gewichtig“ her.
In Bild 17.96 siehst du das wohl bekannteste Baryon – das Proton. Es besteht aus zwei Up-Quarks und einem Down-Quark. Sein Spin ist \(1/2+1/2+1/2=3/2\) und seine Ladung \(+2/3+2/3-1/3=+1\). Das Proton ist das leichteste und einzig stabile Baryon.
In Bild 17.97 siehst du den Aufbau eines Neutrons. Es besteht aus einem Up-Quark und zwei Down-Quarks. Sein Spin ist damit ebenfalls \(1/2+1/2+1/2=3/2\), seine Ladung aber \(+2/3-1/3-1/3=0\) – also elektrisch neutral. Ein freies Neutron (nicht in einem Atomkern gebunden) ist instabil. Es zerfällt mit einer Halbwertszeit von rund 10 Minuten in ein Proton, ein Elektron und ein Elektron-Antineutrino (Betazerfall).
Hier noch eine einfache Merkregel: Drehst du das Zeichen „p“ für ein Proton um, erhältst du ein „d“ und ein Proton enthält genau ein down-Quark. Drehst du das Zeichen „n“ für ein Neutron um, erhältst du ein „u“ und ein Neutron enthält genau ein up-Quark.
17.9.16 Erhaltungssätze
Alle Erhaltungssätze aus der klassischen Physik (Energie, Impuls, Drehimpuls, elektrische Ladung) gelten auch in der Quantenphysik – mit Ausnahme der durch die Unschärferelation möglichen Abweichungen. Darüber hinaus gibt es in der Quantenphysik noch zusätzliche Erhaltungssätze wie die Baryonenzahl, die Leptonenzahl und noch weitere.
Als Beispiel betrachten wir die Erhaltung der Barionenzahl. Die Baryonenzahl, ist als die Differenz der Anzahl von Quarks und Antiquarks, geteilt durch 3 definiert, also:
\[\begin{equation} B={\frac {n_{q}-n_{{\overline {q}}}}{3}} \tag{17.37} \end{equation}\]
Im Experiment zeigt sich, dass in einem abgeschlossenen System die Baryonenzahl stets konstant ist. Wir überprüfen die Erhaltung der Baryonenzahl anhand des Beta-Zerfalls, bei dem sich ein Neutron in ein Proton, Elektron und Neutrino umwandelt. Ein Neutron besteht aus drei Quarks (up, down, down) und die Baryonenzahl ist damit:
\[ B=\frac{n_{q}-n_{{\overline {q}}}}{3} =\frac{3-0}{3}=+1 \]
Ein Proton besteht ebenfalls aus drei Quarks (up, up, down), damit ist die Baryonenzahl auch \(+1\). Die weiteren Zerfallsprodukte (Elektron und Neutrino) sind Elementarteilchen und bestehen aus keinen Quarks, ihre Baryonenzahl ist jeweils \(0\). Die Baryonenzahl ist somit vor und nach dem Zerfall gleich.
Aufgrund der Energieerhaltung können bei einem spontanen „Zerfall“ nur leichtere (massenärmere) Teilchen entstehen. Da das Elektron das massenärmste geladene Lepton ist, gibt es keine Möglichkeit für eine spontane Umwandlung ohne einen der Erhaltungssätze zu verletzen (Stabilität des Elektrons). Ähnliches gilt für das Proton. Es ist das leichteste Baryon und muss daher ebenfalls stabil sein (Stabilität des Protons).












