7.7 Impuls drehender Körper
Bei Experimenten mit rotierenden Gegenständen treten oft (scheinbar) überraschende Effekte auf, die Jung und Alt faszinieren (Bild 7.51).
In diesem Kapitel geht es unter anderem um den Drehimpuls, die Drehimpulserhaltung, Pirouetten und das scheinbar paradoxe Verhalten von Kreiseln.
7.7.1 Drehimpuls
Analog dem Impuls der Translation wird der Drehimpuls (engl. angular momentum) oder „Drall“ als Produkt aus Drehmasse und Winkelgeschwindigkeit (7.2.1 beschrieben.
| \[\begin{equation} \vec{L} = I\cdot\vec{\omega} \tag{7.21} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(\vec{L}\), der Drehimpulsvektor des Körpers (in \(\mathrm{N}\;\mathrm{m}\;\mathrm{s}\))
- \(I\), das Trägheitsmoment des Körpers um die Drehachse (in \(\mathrm{kg}\;\mathrm{m}^2\))
- \(\vec{\omega}\), der Winkelgeschwindigkeit des Körpers (in \(\mathrm{rad/s}\))
Beachte, dass der Drehimpuls ein Vektor ist, der in dieselbe Richtung wie die Winkelgeschwindigkeit zeigt – also entlang der Drehachsenrichtung.
7.7.2 Drehimpulserhaltungssatz
Alle Experimente zeigen, dass nicht nur der lineare Impuls eine Erhaltungsgröße ist, sondern auch der Drehimpuls. Der Drehimpulserhaltungssatz (engl. conservation of angular momentum) lautet:
| Wirken keine äußeren Drehmomente auf ein System, ist der Gesamtdrehimpuls – die Vektorsumme aller Drehimpulse – konstant. |
7.7.3 Drehmoment als zeitliche Drehimpulsänderung
Im Kapitel Impuls hast du gesehen, wie Kraft als zeitliche Impulsänderung beschrieben werden kann. Analog zur Translation lässt sich in der Rotation ein Drehmoment als zeitliche Drehimpulsänderung definieren.
\[\begin{equation} \vec{M} = \frac{\Delta\vec{L}}{\Delta t} \tag{7.22} \end{equation}\]
In dieser Gleichung bedeuten:
- \(\vec{M}\), das Drehmoment (in \(\mathrm{\mathrm{N}\;\mathrm{m}}\))
- \(\Delta\vec{L}\), die Änderung des Drehimpulses (in \(\mathrm{N}\;\mathrm{m}\;\mathrm{s}\))
- \(\Delta t\), die Änderung der Zeit (in \(\mathrm{s}\))
Diese Formulierung ist allgemeiner als die Bewegungsgleichung für die Rotation, denn sie berücksichtigt auch eine Änderung des Trägheitsmoments (zum Beispiel, wenn sich die Drehachse ändert oder die Masse mit der Zeit abnimmt).
7.7.4 Drehmomentstoß
Durch Umschreiben des dynamischen Grundgesetzes für die Rotation erhältst du den Ausdruck:
\[\begin{equation} \Delta\vec{L} = \vec{M}\cdot\Delta t \tag{7.23} \end{equation}\]
In Worten bedeutet diese Gleichung, dass jede Impulsänderung \(\Delta\vec{L}\) durch ein Drehmoment \(\vec{M}\) verursacht wird, das eine gewisse Zeit \(\Delta t\) auf den starren Körper wirkt.
Diese Größe wird Drehmomentstoß (engl. angular impulse) genannt. Der analoge Ausdruck in der Translation ist der Kraftstoß.
7.7.5 Einheit des Drehimpulses
Setzt du in der Definitionsgleichung des Drehimpulses (7.21) ein, erhältst du:
\[ [L] = [I]\cdot [\omega] = 1\;\mathrm{kg}\;\mathrm{m}^2 \cdot\frac{\mathrm{rad}}{\mathrm{s}} = 1\;\frac{\mathrm{kg}\;\mathrm{m}^2}{\mathrm{s}} = 1\;\mathrm{kg}\;\mathrm{m}^2\;\mathrm{s}^{-1} \]
Da der Radiant eine dimensionslose Größe ist, kann seine Angabe bei der Einheit entfallen und wir erhalten die Einheit „Kilogramm Meterquadrat pro Sekunde“.
Die Änderung eines Drehimpulses erfordert immer ein Drehmoment (Drehmomentstoß). Je länger die Wirkdauer des Drehmoments, desto größer fällt die Impulsänderung aus. Die anschaulichere als auch kompaktere Einheit des Drehimpulses ist daher:
\[ [\Delta L] = [M]\cdot[\Delta t] = \mathrm{N}\cdot\mathrm{m}\cdot\mathrm{s} \]
Die Einheit lautet somit „Newton Meter Sekunde“. Durch die Definition der Einheit Newton \(\textrm{N}=\textrm{kg}\cdot\textrm{m}/\textrm{s}^2\) folgt die Gleichheit beider Drehimpuls Einheiten:
\[ \mathrm{N}\cdot\mathrm{m}\cdot\mathrm{s} =\left(\textrm{kg}\cdot\frac{\textrm{m}}{\textrm{s}^2}\right)\cdot\mathrm{m}\cdot\mathrm{s} = \frac{\mathrm{kg}\;\mathrm{m}^2}{\mathrm{s}} \]
7.7.6 Pirouetteneffekt
Der Drehimpuls ist das Produkt aus Trägheitsmoment und Winkelgeschwindigkeit (\(L = I\cdot\omega\)). Verändert sich während der Drehbewegung das Trägheitsmoment – zum Beispiel wird durch Anlegen der Arme an den Körper kleiner – muss aufgrund der Drehimpulserhaltung die Winkelgeschwindigkeit entsprechend größer werden (Bild 7.52).
Dieser Pirouetteneffekt wird in vielen Sportarten wie beim Eiskunstlauf oder Wasserspringen verwendet, um Drehungen zu verlangsamen oder zu beschleunigen.
Links:
7.7.7 Fahrradreifen und Drehschemel
Mit einem Fahrradreifen mit Griffen und einem Drehsessel lässt sich die Drehimpulserhaltung sehr anschaulich zeigen und erfahren (Je größer die Masse des Reifens, desto eindrucksvoller der Effekt).
Sitzt du auf einem Drehsessel und hältst die Drehachse des Reifens senkrecht wie in Bild 7.53 (links) passiert zunächst nichts. Da sich kein Teil dreht, gibt es keinen Drehimpuls und der Gesamtdrehimpuls ist null. Versetzt du den Reifen in Drehung (ohne die Achse zu verändern), beginnst du dich mit dem Drehsessel in die entgegengesetzte Richtung zu drehen. Der Reifen, du und der Drehsessel bilden ein abgeschlossenes System, für das der Drehimpulserhaltungssatz gilt. Damit die Drehimpulserhaltung erfüllt ist und der Gesamtdrehimpuls null bleibt, muss beim Andrehen des Reifens ein gleich großes Drehmoment in entgegengesetzter Richtung auftreten (Bild 7.53, rechts).
Im zweiten Versuch sitzt du ruhig auf dem Sessel und bekommst einen bereits drehenden Reifen von einer zweiten Person ausgehändigt, sodass die Drehachse waagrecht ist. Dein System hat jetzt einen Drehimpuls von außen in waagrechter Richtung erhalten, die senkrechte Komponente des Drehimpulses \(L_z\) ist daher null. Kippst du die Drehachse des Reifens in die senkrechte Position, beginnt sich der Drehsessel in die entgegengesetzte Richtung zu drehen und der Gesamtdrehimpuls in senkrechter Richtung bleibt null (\(\sum F_z=0\)).
Aber muss die waagrechte Drehimpuls-Komponente nicht ebenfalls erhalten bleiben? Das ist richtig! Der Drehsessel lässt aber nur eine Drehung um die senkrechte Achse zu. Der Sessel ist aber mit der Erde verbunden und so ändert das Kippen den Drehimpuls der Erde. Allerdings ist die Masse der Erde so riesengroß gegenüber dem Reifen, dass die Drehimpulsänderung der Erde so unmessbar klein ist.
Links:
7.7.8 Drehen in Schwerelosigkeit
Die Drehimpulserhaltung sorgt für ein interessantes Problem. Stell dir vor, du befindest dich in Schwerelosigkeit. Wie kannst du (ohne dich an einem Gegenstand festzuhalten) deine Orientierung ändern? Jede Drehung des Oberkörpers führt zu einer Gegendrehung des Unterkörpers und umgekehrt. Es scheint unmöglich.
Es gibt aber dennoch eine Möglichkeit. Im Gegensatz zu einem starren Körper können Menschen und Tiere ihre Form verändern. Der Trick besteht darin, das Trägheitsmoment der einen Körperhälfte während der Drehung möglichst groß zu machen und das der anderen Körperhälfte möglichst klein. Bei der Rückdrehung dann umgekehrt.
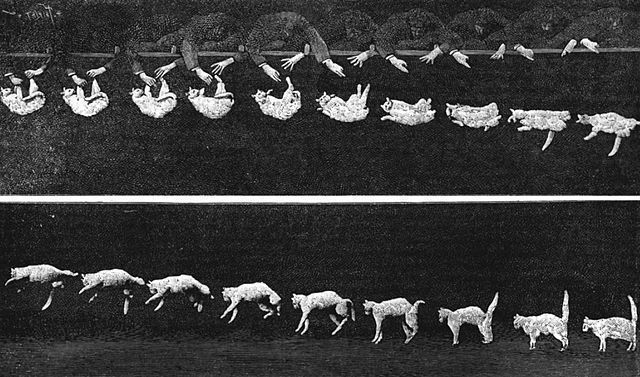
Bild 7.55: Drehung einer Katze in Schwerelosigkeit (Fachzeitschrift Nature, 1894)
Katzen beherrschen diesen Trick und landen sprichwörtlich immer auf ihren Pfoten, unabhängig von ihrer ursprünglichen Orientierung. Im freien Fall führen sie instinktiv die oben beschriebene Bewegung aus, um sicher zu landen (Bild 7.55). Die Drehung des Schwanzes spielt dabei keine Rolle, denn auch Hasen beherrschen diesen Trick.
7.7.9 Freie Kreisel
Einen Kreisel kennst du sicher als Kinderspielzeug. In diesem Abschnitt geht es um sogenannte freie Kreisel. Darunter ist ein Kreisel zu verstehen, der so aufgehängt ist, dass er sich in jede beliebige Richtung frei drehen kann (es wirken also keine äußeren Drehmomente). Eine solche Aufhängung (Bild 7.56) wird nach Gerolamo Cardano als kardanische Aufhängung (engl. gimbal) bezeichnet.
Für einen freien Kreisel ist der Drehimpuls (Größe und Richtung des Drehimpulsvektors) immer konstant. Einmal in Rotation versetzt, zeigt die Rotationsachse immer in dieselbe Richtung im Raum. Wird am Äquator die Kreiselachse zum Beispiel senkrecht eingestellt, zeigt die Kreiselachse immer an dieselbe Stelle am Fixsternhimmel, auch nach Stunden. So kann gezeigt werden, dass die Erde rotiert und der Fixsternhimmel nicht rotiert!
7.7.10 Präzessionsbewegung
In diesem Abschnitt beschäftigen wir uns mit Kreiseln, auf die ein äußeres Drehmoment wirkt. Wird ein rotierender Kreisel wie in Bild 7.57 horizontal aufgehängt, fällt er erstaunlicherweise nach dem Loslassen nicht zu Boden.
Zu Beginn hat der Kreisel den Drehimpuls \(L\). Die Gewichtskraft \(F_\text{G}\) erzeugt um den Drehpunkt \(P\) ein Drehmoment \(M\). Es bewirkt während der kurzen Zeit \(\Delta t\) eine Impulsänderung \(\Delta L = M\cdot\Delta t\). Der resultierende neue Drehimpuls des Kreisels ist \(L^\prime\).
Die Kreiselachse weicht also im rechten Winkel zu \(F\) aus. Diese Bewegung wird Präzession (engl. precession) genannt. Die Bezeichnung ist abgeleitet von dem lateinischen Wort praecessio für „das Vorangehen“ – nicht zu verwechseln mit dem Wort Präzision (Genauigkeit). Beachte: Je schneller der Kreisel dreht (je größer der Drehimpuls), desto langsamer ist die Präzessionsbewegung.
Da die Zeiten \(\Delta t\) sehr klein sind, bleibt die Größe (Länge) des Drehimpulsvektors \(L\) während der Präzessionsbewegung unverändert, nur die Richtung ändert sich dabei.
Bei einem schräg gestellten Kreisel beschreibt die Achse bei der Präzessionsbewegung einen Kegelmantel.
Links:
7.7.11 Nutationsbewegung
Die rotierende Erde verhält sich wie ein riesiger Kreisel im Weltall. Da die Rotationsachse der Erde gegen die Ekliptik geneigt ist, führen die Gezeitenkräfte durch die Sonne zu einer Präzessionsbewegung des Erdkreisels. Zusätzlich führen die Gezeitenkräfte des Mondes auf die Erde zu einer Störung dieser Präzessionsbewegung. Die daraus resultierende Bewegung siehst du in Bild 7.58 (Effekt der Störung stark überzeichnet!).
Diese der Präzession \(P\) überlagerte Nick-Bewegung \(N\) wird Nutation (engl. nutation) genannt. Die Bezeichnung ist abgeleitet von dem lateinischen Wort nutare für „nicken“.
7.7.12 Drehimpuls eines Teilchens
Befindet sich ein Körper sehr weit vom Drehzentrum entfernt, kann er als einzelner Massenpunkt angenähert werden. In diesem Fall lautet der Zusammenhang von linearem Impuls und Drehimpuls eines annähernd punktförmigen Körpers (engl. angular momentum of a point particle):
| \[\begin{equation} \vec{L} = \vec{r}\times\vec{p} = m\cdot \vec{r}\times\vec{v} \tag{7.24} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(\vec{L}\), der Drehimpulsvektor des Körpers (in \(\mathrm{kg\cdot m^2 /s}\))
- \(\vec{r}\), der Radiusvektor vom Drehzentrum zum Körper (in \(\mathrm{m}\))
- \(\vec{p}\), der (lineare) Impulsvektor (\(\vec{p}=m\cdot\vec{v}\)) des Körpers (in \(\mathrm{kg\cdot m/s}\))
Als Kreuzprodukt steht der Drehimpulsvektor zu allen Zeiten im rechten Winkel sowohl auf den Radiusvektor als auch auf den Impulsvektor (oder Bahngeschwindigkeitsvektor).
7.7.13 Herleitung: Drehimpuls eines Teilchens
Im Folgenden gehen wir von der vereinfachten Annahme aus, dass sich die Masse auf einer Kreisbahn um ein Zentrum bewegt. In diesem Spezialfall stehen Impulsvektor und Radiusvektor stets im rechten Winkel zueinander und der Betrag des Drehimpulses eines Massenpunkts lautet dann \(L=r\cdot p\).
Das Trägheitsmoment einer punktförmigen Masse lautet:
\[ I = m\cdot r^2 \]
Die Bahngeschwindigkeit hängt mit der Winkelgeschwindigkeit wie folgt zusammen:
\[ \begin{aligned} v = {} & r\cdot\omega &&\qquad\Bigr\rvert\cdot \frac{1}{r}\\ \frac{v}{r} = {} & \omega \\ \end{aligned} \]
Setzen wir beides in die Formel für den Drehimpuls (7.21) ein, erhalten wir:
\[ \begin{aligned} L = {} & I\cdot \omega \\ L = {} & (m\cdot r^{\cancel{2}})\cdot \frac{v}{\cancel{r}} \\ L = {} & m\cdot r\cdot v \\ L = {} & r\cdot m\cdot v &&\qquad\Bigr\rvert\quad p = m\cdot v\\ L = {} & r\cdot p \\ \end{aligned} \]
Also den gesuchten Zusammenhang von Bahndrehimpuls \(L\) und linearem Impuls \(p\) eines Teilchens.
7.7.14 Bahndrehimpuls und Eigendrehimpuls
Ein typischer Fall, bei dem du die Formel für den Drehimpuls eines annähernd punktförmigen Körpers verwendet werden darfst, ist der Drehimpuls eines Planeten um seinen Zentralstern (oder eines Mondes um seinen Planeten). In diesem Fall wird der Drehimpuls als Bahndrehimpuls (engl. orbital angular momentum) bezeichnet.
Dreht sich der Himmelskörper auch noch um die eigene Achse, gibt es einen zweiten zusätzlichen Drehimpuls. Dieser wird – um ihn vom Bahndrehimpuls zu unterscheiden – Eigendrehimpuls (engl. spin angular momentum) genannt. In der Quantenmechanik entspricht der Eigendrehimpuls der Eigenschaft Spin.
Die Gezeitenkräfte verformen einen Himmelskörper. Dreht sich der Körper dabei, wird der Himmelskörper „durchgewalkt“ und ein Teil der Rotationsenergie wird in Wärme umgewandelt (Gezeitenreibung). Wird die Rotationsenergie kleiner, nimmt die Drehgeschwindigkeit ab. Genau das passiert zum Beispiel im System Erde-Mond. Durch die Gezeitenreibung nimmt die Drehgeschwindigkeit der Erde ab und die Tageslänge somit zu. Aber keine Sorge: In 100 Jahren sind das nur etwa \(0{,}002\;\mathrm{s}\). Nach dem Drehimpulserhaltungssatz muss der Gesamtdrehimpuls aber erhalten bleiben. Da der Eigendrehimpuls der Erde kleiner wird, nimmt der Bahndrehimpuls des Mondes zu. Die Umlaufbahn des Mondes vergrößert sich deswegen um rund \(3{,}8\;\mathrm{cm}\) pro Jahr.