7.6 Bewegungsenergie drehender Körper
Ein Stromausfall während einer Operation kann Menschenleben kosten. Daher haben Krankenhäuser einen Notstrom-Dieselgenerator, der im Falle eines Stromausfalls einspringt. Dabei gibt es allerdings ein Problem. Der Dieselgenerator kann nicht so schnell anspringen, um eine unterbrechungsfreie Stromversorgung zu garantieren. Daher befindet sich im Keller des Krankenhauses eine große zylinderförmige Masse, die ständig in Rotation gehalten wird. Sobald ein Blackout eintritt, überbrückt die in der rotierenden Masse gespeicherte Energie die kurze Zeitspanne, bis der Dieselgenerator übernehmen kann.
In diesem Kapitel wirst du die Drehmasse kennenlernen, sowie die Bewegungsenergie von rotierenden und rollenden Körpern.
7.6.1 Rotationsenergie
Die Rotationsenergie (engl. rotational energy) eines starren Körpers um eine Achse \(a\) lautet:
Rotationsenergie eines starren Körpers: \[\begin{equation} E_\text{ROT} = I\cdot\frac{\omega^2}{2} \tag{7.15} \end{equation}\] |
In dieser Formel bedeuten:
- \(E_{\text{ROT}}\), die Rotationsenergie des Körpers um die Drehachse \(a\) (in \(\mathrm{J}\))
- \(I\), das Trägheitsmoment des Körpers um die Drehachse \(a\) (in \(\mathrm{kg}\;\mathrm{m}^2\))
- \(\omega\), die Winkelgeschwindigkeit des Körpers (in \(\mathrm{rad}/\mathrm{s}\))
Die Formel für die translatorische kinetische Energie (\(m\cdot v^2/2\)) und die Formel für die Rotationsenergie haben dieselbe Form. Es müssen nur die translatorischen Größen (Masse und Geschwindigkeit) gegen die entsprechenden Größen der Rotation (Drehmasse und Winkelgeschwindigkeit) ersetzt werden.
7.6.2 Trägheitsmoment (Drehmasse)
Das Trägheitsmoment \(I\) (engl. moment of inertia) ist ein Maß für den Widerstand gegen die Änderung einer Drehbewegung eines starren Körpers um eine bestimmte Drehachse.
Ist ein Körper aus den Massenstücken \(m_1,m_2,\ldots,m_i,\ldots\) aufgebaut, berechnet sich sein Trägheitsmoment aus der Summe
| \[\begin{equation} I=m_1\cdot r_1^2 + m_2\cdot r_2^2 + \ldots + m_i\cdot r_i^2 + \ldots = \sum m_i\cdot r_i^2 \tag{7.16} \end{equation}\] |
wobei die Größen \(r_1,r_2,\ldots,r_i,\ldots\) die Abstände der Massen von der Drehachse sind. Ein und derselbe Körper hat also unterschiedliche Trägheitsmomente, je nachdem, wo sich die Drehachse befindet!
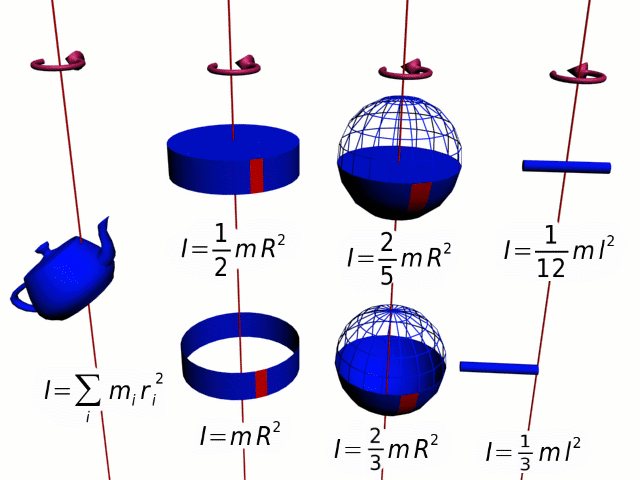
Für einfache geometrische Körper wie Kugel, Zylinder oder Quader können Drehmomente durch unendliche Summen (Integrale) berechnet werden. In Bild 7.40 siehst du einige Ergebnisse dieser Berechnungen.
Für kompliziertere Körper wird das Drehmoment experimentell bestimmt.
Links:
7.6.3 Einheit des Trägheitsmoments
Um auf die Einheit des Trägheitsmoments zu erhalten, setzen wir in seine Definitionsgleichung ein:
\[ [I] = [m]\cdot [r]^2 = 1\;\mathrm{kg}\;\mathrm{m}^2 \]
Die Einheit „Kilogramm Quadratmeter“ hat keinen eigenen Namen.
7.6.4 Herleitung der Rotationsenergie
Wir stellen uns einen starren Körper aus lauter kleinen Massenstücken \(m_1,m_2,\ldots,m_i,\ldots\), die sich jeweils im Abstand \(r_1,r_2,\ldots,r_i,\ldots\) von der Drehachse befinden (Bild 7.41).
Bei einer Rotation bewegt sich jedes der Massenstücke mit seiner Tangentialgeschwindigkeit \(v_1,v_2,\ldots,v_i,\ldots\) um die Drehachse. Die kinetische Energie des rotierenden Körpers \(E_\text{ROT}\) ist die Summe der einzelnen kinetischen Energien seiner Massenstücke.
\[ \begin{aligned} E_\text{ROT} = {} & \frac{m_1\cdot v_1^2}{2} + \frac{m_1\cdot v_1^2}{2} + \ldots + \frac{m_i\cdot v_i^2}{2} + \ldots\\ \end{aligned} \]
Winkelgeschwindigkeit und Tangentialgeschwindigkeit eines Massenpunktes hängen über die Beziehung \(v_i=\omega\cdot r_i\) zusammen (Gleichungen (7.8)). Da es sich um einen starren Körper handelt, ist die Winkelgeschwindigkeit \(\omega\) für alle Massenstücke gleich groß.
\[ \begin{aligned} E_\text{ROT} = {} & \frac{m_1\cdot (\omega\cdot r_1)^2}{2} + \frac{m_2\cdot (\omega\cdot r_2)^2}{2} + \ldots + \frac{m_i\cdot (\omega\cdot r_i)^2}{2} + \ldots\\ E_\text{ROT} = {} & \frac{m_1\cdot r_1^2\cdot \omega^2}{2} + \frac{m_2\cdot r_2^2\cdot \omega^2}{2} + \ldots + \frac{m_i\cdot r_i^2\cdot \omega^2}{2} + \ldots\\ E_\text{ROT} = {} & (m_1\cdot r_1^2 + m_2\cdot r_2^2 + \ldots + m_i\cdot r_i^2 + \ldots)\cdot\frac{\omega^2}{2}\\ \end{aligned} \]
Mit der Bezeichnung
\[ I=m_1\cdot r_1^2 + m_2\cdot r_2^2 + \ldots + m_i\cdot r_i^2 + \ldots \]
erhältst du für die Rotationsenergie eines starren Körpers den Ausdruck:
\[ E_\text{ROT} = I\cdot\frac{\omega^2}{2} \]
7.6.5 Rotationsenergie Dimensionsprobe
Wenn der Ausdruck für die Rotationsenergie einer Energie entspricht, muss er die Energieeinheit Joule ergeben.
Bei einer Dimensionsprobe können alle dimensionslosen Faktoren weggelassen werden. Außerdem ist der Radiant eine dimensionslose Größe und es gilt \(\mathrm{rad}/\mathrm{s}=\mathrm{1}/\mathrm{s}\). Setzt du ein, erhältst du:
\[ \begin{aligned} {}[E_\text{ROT}] = {} &{\frac {1}{2}}\cdot [I]\cdot[\omega]^{2} \\ = {} & 1\;(\mathrm{kg}\cdot\mathrm{m}^2)\cdot\left(\frac{1}{\mathrm{s}^2}\right) \\ = {} & 1\;\mathrm{kg}\cdot\frac{\mathrm{m}^2}{\mathrm{s}^2} \\ = {} & 1\;\mathrm{kg}\cdot\frac{\mathrm{m}}{\mathrm{s}^2}\cdot\mathrm{m} &&\qquad\Bigr\rvert\ 1\;\mathrm{N}=1\;\mathrm{kg}\cdot\frac{\mathrm{m}}{\mathrm{s}^2}\\ = {} & 1\;\mathrm{N}\cdot\mathrm{m} \\ = {} & 1\;\mathrm{J} \\ \end{aligned} \]
Der letzte Schritt folgt aus der Definition der Arbeit. Damit ist gezeigt, dass der Ausdruck für die Rotationsenergie auch wirklich die Einheit einer Energie hat.
7.6.6 Anwendungsbeispiel: Wettrennen rotierender Körper
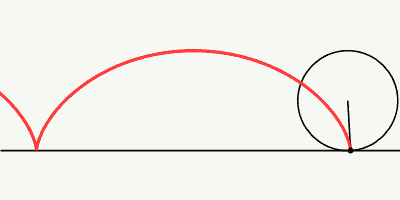
In Bild 7.42 siehst du den Wettlauf unterschiedlicher runder Körper beim bergab rollen.
Alle Körper haben die gleiche Masse. Somit wirkt auf alle Körper die gleiche Gewichtskraft. Da alle Körper rotationssymmetrisch sind und gleich großen Radius besitzen, ist der Abstand Auflagepunkt zu Massenmittelpunkt ebenfalls gleich groß. Damit ist auch das durch die Gewichtskraft verursachte Drehmoment bei allen Körpern auf der schiefen Ebene gleich groß. Allerdings besitzen die Körper unterschiedliche Trägheitsmomente:
\[\begin{eqnarray} I_{\text{Vollkugel}} & = & \frac{2}{5}\cdot m \cdot r^2 \\ I_{\text{Vollzylinder}} & = & \frac{1}{2} \cdot m \cdot r^2 \\ I_{\text{Hohlkugel}} & = & \frac{2}{3}\cdot m \cdot r^2 \\ I_{\text{Hohlzylinder}} & = & m \cdot r^2 \\ \end{eqnarray}\]
Damit stehen die Trägheitsmomente in folgendem Verhältnis:
\[ I_{\text{VK}} : I_{\text{VZ}} : I_{\text{HK}} : I_{\text{HZ}} = \frac{2}{5} : \frac{1}{2} : \frac{2}{3} : 1 = 0{,}4 : 0{,}5 : 0{,}\dot6 : 1 \]
Da die Vollkugel von allen Körpern in Bild 7.42 das kleinste Trägheitsmoment besitzt, kann sie bei gleichem Drehmoment am schnellsten in Rotation versetzt werden – sie bietet den kleinsten Widerstand gegen eine Drehbewegungsänderung. Damit gewinnt sie das Wettrennen. Alle weiteren Plätze werden von den Körpern mit aufsteigendem Trägheitsmoment belegt.
7.6.7 Satz von Steiner
Der Satz von Steiner oder das Parallelachsen-Theorem (engl. parallel axis theorem) gestattet es, das Trägheitsmoment um eine Achse zu berechnen, wenn sein Trägheitsmoment für eine dazu parallele Achse bereits bekannt ist.
Die Formel lautet (ohne Herleitung):
\[\begin{equation} I_{a''} = I_{a'} + m\cdot d^2 \tag{7.17} \end{equation}\]
In der Gleichung bedeuten:
- \(I_{a'}\), das bereits bekannte Trägheitsmoment um die Achse \(a'\) (in \(\mathrm{kg\cdot m^2}\))
- \(m\), die Masse des Körpers (in \(\mathrm{kg}\))
- \(d\), der Normalabstand der Achsen (in \(\mathrm{m}\))
- \(I_{a''}\), das Trägheitsmoment um die zu Achse \(a'\) parallele Achse \(a''\) (in \(\mathrm{kg\cdot m^2}\))
Aus dem Bild 7.43 kannst du erkennen, was hinter dem Satz von Steiner steckt. Die Drehung eines Körpers um die Achse \(a''\) lässt sich durch eine Drehung des Massenmittelpunktes um diese Achse (die Orientierung der Hantel im Raum bleibt dabei gleich) gefolgt von einer Drehung des Körpers um die Achse \(a'\) auffassen.
In der Praxis lassen sich unregelmäßige Körper durch Unterteilung in einfache Formen annähern. In Tabellen findest du Trägheitsmomente für solche einfachen Formen (Bild 7.40) und, mit dem Satz von Steiner lassen sich diese Formeln für die Trägheitsmomente für die jeweilige Situation anpassen.
7.6.8 Anwendungsbeispiel: Satz von Steiner
Das Trägheitsmoment für einen Stab, der um eine Achse durch seinen Mittelpunkt rotiert (Bild 7.40), ist durch folgende Formel gegeben:
\[ I = \frac{1}{12}\cdot m\cdot \ell^2 \]
In diesem Beispiel interessiert uns das Trägheitsmoment desselben Stabs, wenn er um sein Ende rotiert (Bild 7.44).
In diesem Fall ist der Normalabstand der beiden (parallelen) Achsen genau \(\ell/2\) und wir erhalten nach dem Satz von Steiner:
\[\begin{align} I' = {} & I + m \cdot \left(\frac{\ell}{2}\right)^2 \notag \\ I' = {} & I + m \cdot \frac{\ell^2}{4} \notag \\ I' = {} & \frac{1}{12}\cdot m\cdot \ell^2 + \frac{1}{4}\cdot m \cdot \ell^2 &&(\text{herausheben}) \notag \\ I' = {} & \left(\frac{1}{12}+\frac{1}{4}\right)\cdot m\cdot \ell^2 &&(\text{erweitern}) \notag \\ I' = {} & \left(\frac{1}{12}+\frac{3}{12}\right)\cdot m\cdot \ell^2 \notag \\ I' = {} & \frac{4}{12}\cdot m\cdot \ell^2 &&(\text{kürzen}) \notag \\ I' = {} & \frac{1}{3}\cdot m\cdot \ell^2 \notag \\ \end{align}\]
Das ist derselbe Ausdruck, den du bereits aus der Tabelle der ausgewählten Trägheitsmomente kennst.
7.6.9 Bewegungsgleichung für die Rotation
Mit dem Trägheitssatz (\(F=m\cdot a\)) hast du die Bewegungsgleichung für die Translation kennengelernt. Mit dem Trägheitsmoment lässt sich eine analoge Bewegungsgleichung für die Rotation formulieren.
| \[\begin{equation} M = I\cdot\alpha \tag{7.18} \end{equation}\] |
Wirkt ein Drehmoment \(M\) auf einen Körper, ändert sich seine Winkelgeschwindigkeit (das entspricht einer Winkelbeschleunigung \(\alpha\)). Je größer das Trägheitsmoment, desto kleiner ist die Winkelbeschleunigung bei gleichem Drehmoment.
7.6.10 Rollwettlauf und Balancierstange
Je weiter die Masse eines Körpers von der Drehachse entfernt ist, desto größer ist sein Trägheitsmoment. Deshalb setzt sich der Hohlzylinder, dessen gesamte Masse am Umfang konzentriert ist, langsamer in Bewegung als ein Vollzylinder, dessen Masse auf das gesamte Zylindervolumen gleichmäßig verteilt ist (Animation 7.42 am Kapitelanfang).
In Bild 7.45 siehst du ein weiteres Anwendungsbeispiel: Je größer das Trägheitsmoment, desto langsamer beginnt eine Drehbewegung. Wenn du die Arme ausbreitest oder sogar eine Balancierstange verwendest, erhöhst du dein Trägheitsmoment, und du hast mehr Zeit, eine Drehbewegung auf dem Seil/Slackline auszugleichen.
7.6.11 Freie Achsen und Unwucht
Wählst du bei einem Körper eine beliebige Drehachse für die Rotation aus, hast du in den meisten Fällen eine Unwucht. Als Unwucht werden Kräfte bezeichnet, die auf das Lager und die Achse wirken. Bei diesen Kräften kannst du folgende zwei Arten unterscheiden:
statische Unwucht: Die Drehachse geht nicht durch den Massenmittelpunkt. Es kommt zu einer radialen Nettokraft auf die Achse (Bild 7.46-a). Eine statische Unwucht ist ohne Rotation feststellbar.
dynamische Unwucht: Die Drehachse verläuft zwar durch den Massenmittelpunkt, aber es kommt zu einem seitlichen Drehmoment (Bild 7.46-b). Die dynamische Unwucht kann nur bei einem rotierenden Körper festgestellt werden.
Treten bei der Rotationsachse eines Körpers weder statische noch dynamische Unwucht auf, dreht sich der Körper um eine freie Achse (gemeint ist „frei von Kräften“). Das Anbringen von Zusatzmassen („auswuchten“) schafft eine freie Achse.
7.6.12 Rotation ohne feste Achse
Bisher sind wir bei allen starren Körpern immer von einer fix vorgegebenen Rotationsachse ausgegangen. In diesem Abschnitt beantworten wir die Frage, um welche Achse sich ein Körper dreht, wenn keine Achse vorgegeben wird. Wirfst du einen Quader (etwa ein Buch) in die Luft, erfolgt die Drehung immer um den Massenmittelpunkt. In den meisten Fällen beginnt der Quader aber zu torkeln – die Drehachse ändert sich während der Rotation also ständig.
Wir hängen einen Quader an der kleinsten Fläche auf und versetzen den Körper in Drehung (7.47-1). In dieser Position ändert der Körper seine Drehachse nicht – seine Rotationsachse ist stabil. Bei der Achse \(a_1\) handelt es sich um die freie Achse mit dem kleinsten Trägheitsmoment.
Wird der Körper während dieser Rotation durch einen Stoß gestört (7.47-2), beginnt er sich um die Achse \(a_3\) zu drehen (7.47-3). Bei dieser Achse handelt es sich um die freie Achse mit dem größten Trägheitsmoment. Wird der Körper bei Rotation um diese Achse gestört, kehrt er immer wieder zur Achse \(a_3\) zurück (7.47-4).
| Nur die Drehungen um die freien Achsen mit dem kleinsten und dem größten Trägheitsmoment sind stabil. |
7.6.13 Rollbewegung starrer Körper
Wenn ein Körper auf einer Unterlage rollt (Animation 7.48), ist das nicht dasselbe wie ein rotierender Körper, wie wir ihn bisher betrachtet haben.
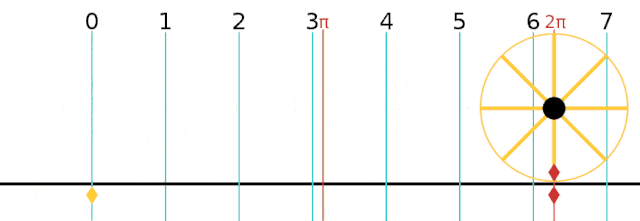
In der Animation ist ein Punkt am Rand des Körpers markiert. Die Kurve, die dieser Punkt beim Abrollen des Körpers beschreibt, wird Zykloide oder Rollkurve genannt. Wenn du den Punkt verfolgst, kannst du sehen, dass der Punkt für einen kurzen Moment stillzustehen scheint, immer wenn er den Boden berührt.
Der Drehpunkt bei dieser Bewegung ist nämlich kein fixer Punkt am Körper, sondern jeweils der momentane Berührungspunkt von Körper und Unterlage. Ein einziger Punkt bleibt immer auf derselben Höhe. Das ist der Mittelpunkt des Rades. Jede Rollbewegung kann daher als eine Kombination aus einer Translation des Mittelpunktes und einer Rotation um diesen Punkt beschrieben werden.
Unabhängig von der Geschwindigkeit hat der Radmittelpunkt nach einer vollen Umdrehung des Rades (\(\varphi = 2\pi\;\mathrm{rad}\)) einen Weg \(s_M=r\cdot2\pi\) zurückgelegt (Bild 7.49 für das Einheitsrad \(r=1\)). Für einen Körper, der ohne zu rutschen („schlupflos“) abrollt, muss daher die folgende Rollbedingung gelten:
\[ s_M=r\cdot\varphi \]
Dividieren wir durch die Zeit, erhalten wir die folgende Beziehung zwischen Geschwindigkeit des Radmittelpunktes und der Winkelgeschwindigkeit des Rades:
\[\begin{equation} v_M=r\cdot\omega \tag{7.19} \end{equation}\]
Links:
7.6.14 Bewegungsenergie rollender Körper
Eine Rollbewegung ist keine reine Rotation, sondern eine Kombination aus Translation und Rotation. Daher ist auch die Bewegungsenergie eines rollenden Körpers die Summe aus seiner translatorischen kinetischen Energie und einer Rotationsenergie (Bild 7.50).
Genauer gesagt ist die gesamte Bewegungsenergie eines rollenden starren Körpers die Summe aus der
- Rotationsenergie um den Massenmittelpunkt_ und der
- translatorischen kinetischen Energie der Gesamtmasse konzentriert im Massenmittelpunkt.
\[ E_\mathrm{GES} = \frac{1}{2}\cdot I_{MM}\cdot \omega^2 +\frac{1}{2}\cdot m\cdot v_{MM}^2 \]
Mithilfe der Rollbedingung ((7.19))
\[ v_{MM} = r\cdot \omega \]
können wir die Gleichung weiter vereinfachen:
\[\begin{equation} \begin{aligned} E_\mathrm{GES} = {} & \frac{1}{2}\cdot I_{MM}\cdot \left(\frac{v_{MM}}{r}\right)^2 +\frac{1}{2}\cdot m\cdot v_{MM}^2 \\ = {} & \frac{1}{2}\cdot I_{MM}\cdot \frac{v_{MM}^2}{r^2} +\frac{1}{2}\cdot m\cdot v_{MM}^2 \\ = {} & \frac{1}{2}\cdot\left(\frac{I_{MM}}{r^2}+m\right) \cdot v_{MM}^2 \end{aligned} \tag{7.20} \end{equation}\]
Links: