7.5 Seil- und Flaschenzüge
Seil- und Flaschenzüge sind spätestens seit der Antike bekannt und finden auch heute noch zahlreich Anwendung. Unter anderem beim Klettern (Bild 7.29).
Seil- und Flaschenzüge sind Anwendungen des Hebelgesetzes. Diese einfachen Maschinen bestehen aus einer Kombination aus Rollen (Zahnrädern) und Seilen (Ketten), mit dem Ziel, Kräfte umzuleiten und/oder die Kraft für eine mechanische Arbeit zu verkleinern. Für alle Seil- und Flaschenzüge gilt immer „die goldene Regel der Mechanik“: Auch wenn die Kraft verkleinert wird, die verrichtete Arbeit ist immer gleich groß!
Für alle Überlegungen in diesem Abschnitt gehen wir immer von masselosen und reibungsfreien Rollen aus. In der Praxis steigt jedoch die Lagerreibung mit der Anzahl der Rollen und beschränkt somit die Wirkung von Seil- und Flaschenzügen.
7.5.1 Feste Rolle
Als feste Rolle (engl. fixed pulley) wird eine Rolle bezeichnet, die an einer Wand oder Decke montiert ist und die bei der Verwendung am selben Ort bleibt.
Eine einfache feste Rolle (Bild 7.30) entspricht einem zweiseitigen Hebel, bei dem der Lastarm (\(r\)) und der Kraftarm (\(r\)) dieselbe Länge haben (den Radius der Rolle). Daher führt eine feste Rolle zu keiner Krafterleichterung – die Kraft wird lediglich in eine andere Richtung umgelenkt. Daher wird eine feste Rolle auch als Umlenkrolle bezeichnet.
Beachte, dass auf die Befestigung an der Wand/Decke, an der die feste Rolle montiert ist, die doppelte Kraft wirkt!
7.5.2 Lose Rolle
Lose Rollen (engl. moveable pulley) sind Rollen, die sich mit der Last mitbewegen.
Eine einfache lose Rolle (Bild 7.31) entspricht einem einseitigen Hebel. Der Drehpunkt (\(D\)) befindet sich am Rand der Rolle. Der Lastarm (\(r\)) entspricht dem Radius der Rolle und der Kraftarm (\(2r\)) entspricht dem Durchmesser der Rolle. Die Krafterleichterung entspricht dem Verhältnis von Radius zu Durchmesser, also 1:2. Im selben Verhältnis verlängert sich der Weg: Um die Last \(1\;\mathrm{m}\) Meter zu heben, muss das Seil \(2\;\mathrm{m}\) gezogen werden.
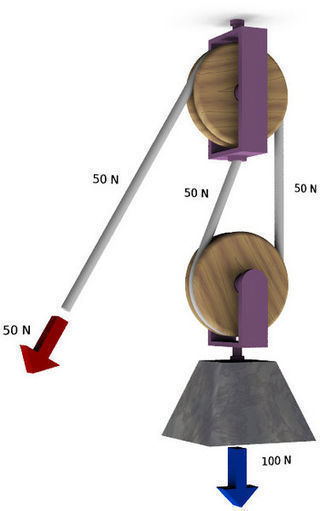
In unserem Beispiel muss nach oben gezogen werden, um die Masse zu heben. Das ist in vielen Fällen unpraktisch. Daher wird zusätzlich eine feste Rolle verwendet, um die Kraft umzulenken (Bild 7.32).
Da die feste Rolle lediglich die Richtung der Kraft ändert, ist die Krafterleichterung gleich groß wie bei der einfachen losen Rolle. Beachte, dass bei dieser Anordnung auf die Wand/Decke, an der die feste Rolle montiert ist, die 1,5-fache der Gewichtskraft wirkt (also in unserem Beispiel \(150\;\mathrm{N}\))! Dabei macht es keinen Unterschied, ob das Seilende an der festen Rolle montiert ist (wie in Bild 7.32), oder an der Wand/Decke – die Kraft bleibt dieselbe.
7.5.3 Flaschenzug
Im Abschnitt lose Rolle hast du gesehen, dass eine einfache lose Rolle den Kraftaufwand zum Heben einer Masse halbiert. Bei einem Flaschenzug (engl. block and tackle) wird durch Hinzufügen von weiteren loser und fester Rollen der Kraftaufwand weiter verkleinert. Nach der Art der Kraftübersetzung können folgende Bauformen von Flaschenzügen unterschieden werden, die in den folgenden Abschnitten genauer besprochen werden:
Der Name Flaschenzug kommt von der Halterung der Rollen, die in der Fachsprache als Block oder Flasche bezeichnet werden (Bild 7.33).
Flaschenzugsysteme können oft recht kompliziert sein. Die beste Strategie, um die Kraftersparnis eines Flaschenzuges zu bestimmen, ist, sich den Weg-Zuwachs zu überlegen!
7.5.4 Faktorenflaschenzug
Die einfachste Bauform eines Flaschenzugs ist der Faktorenflaschenzug.
Ganz links (Bild 7.34-1) siehst du eine feste Rolle mit der Kraftübersetzung 1:1. Daneben (Bild 7.34-2) siehst du zusätzlich eine lose Rolle wie in Abschnitt mit der Kraftübersetzung 1:2. Im dritten Bild (Bild 7.34-3) wird eine weitere Rolle hinzugefügt. Die Last verteilt sich jetzt auf 3 Seile und damit ergibt sich eine Kraftübersetzung von 1:3. Im letzten Bild (Bild 7.34-4) wird eine vierte Rolle hinzugefügt. Die Last verteilt sich jetzt auf 4 Seile und damit ergibt sich eine Kraftübersetzung von 1:4.
Beachte: Die Gewichtskraft der Last teilt sich auf die Seilstücke gleichmäßig auf. Bei einem Faktorenflaschenzug herrscht in jedem Seilstück dieselbe Zugkraft.
Die Kraft auf die Deckenaufhängung ist jeweils die Summe aus Gewichtskraft der zu hebenden Last und der Zugkraft am losen Ende. Im Bild 7.34 sind das (von links nach rechts)
- \(100\;\mathrm{N}+100\;\mathrm{N}=200\;\mathrm{N}\),
- \(100\;\mathrm{N}+50\;\mathrm{N}=150\;\mathrm{N}\),
- \(100\;\mathrm{N}+33\,1/3\;\mathrm{N}=133\,1/3\;\mathrm{N}\) und
- \(100\;\mathrm{N}+25\;\mathrm{N}=125\;\mathrm{N}\).
Im Bild 7.35 siehst du in der oberen Hälfte drei Faktorenflaschenzüge mit eins, zwei und vier Rollen. In der unteren Hälfte siehst du, wie die Rollen eines Faktorenflaschenzuges oben und unten kompakt auf eine Achse gelegt und dann zueinander verdreht werden. In dieser Bauform wird der Faktorenflaschenzug in der Praxis meistens verwendet.
Der Name Faktorenflaschenzug kommt von dem Verhältnis von Anzahl der Rollen und Kraftersparnis: Bei \(n\) Rollen sinkt der Kraftaufwand auf \(1/n\) und der Weg erhöht sich um den Faktor \(n\).
7.5.5 Potenzflaschenzug
Der Potenzflaschenzug (engl. spanish burton) besteht nur aus losen Rollen und einer festen Rolle (Umlenkrolle).
Vorsicht: Anders als bei dem Faktorenflaschenzug ergibt sich die Kraftersparnis nicht durch die Anzahl der Seile, an denen die Last hängt! Das liegt daran, dass in den Seilen unterschiedliche Zugkräfte wirken. Im Bild 7.36 links siehst du, wie sich die Gewichtskraft der Last auf zwei Seile aufteilt. In der oberen losen Rolle teilt sich die halbe Gewichtskraft der Last wieder auf zwei Seile auf, sodass die Zugkraft nur noch 1/4 der Gewichtskraft der Last wirkt.
Der Effekt lässt sich durch Hinzufügen von weiterer loser Rollen verstärken (Bild 7.36, rechts). Bei \(n\) Rollen ergibt sich daher eine Kraftersparnis von \(1/2^n\) und eine Weg-Verlängerung um \(2^n\), daher auch der Name Potenzflaschenzug.
Die Kraft auf die Decke ergibt sich als Summe der Kräfte auf die einzelnen Aufhängungen. Für unsere beiden Fälle ergeben sich die Kräfte (immer von links nach rechts):
- \((20\;\mathrm{N}+20\;\mathrm{N})+20\;\mathrm{N}+40\;\mathrm{N}=100\;\mathrm{N}=20\;\mathrm{N}+80\;\mathrm{N}\)
- \((10\;\mathrm{N}+10\;\mathrm{N})+10\;\mathrm{N}+20\;\mathrm{N}+40\;\mathrm{N}=90\;\mathrm{N}=10\;\mathrm{N}+80\;\mathrm{N}\)
Auch hier ist die Gesamtkraft auf die Decke die Summe aus Zugkraft am losen Ende und Gewichtskraft der Last.
7.5.6 Differenzialflaschenzug
Anders als die bisherigen Flaschenzüge besteht der Differenzialflaschenzug (engl. differential pulley) aus zwei festen Rollen, die fest miteinander verbunden sind und unterschiedliche Durchmesser haben. Die Last hängt an einer losen Rolle (Bild 7.37). Bei diesem Flaschenzugtyp wird ein durchgehendes Seil verwendet, dessen Länge vom Übersetzungsverhältnis nahezu unabhängig ist.
Es kann gezeigt werden, dass das Kräfteverhältnis beim Differentialflaschenzug lautet:
\[\begin{equation} 1:\frac{2R}{R-r} \tag{7.14} \end{equation}\]
An dem Ausdruck kannst du erkennen, dass das Verhältnis von der Differenz der Radien der beiden festen Rollen abhängt. Von dieser Eigenschaft leitet sich der Name für diesen Flaschenzug ab.
Da die Spannung im Seil nicht überall gleich groß ist, muss sichergestellt werden, dass ein rutschfester Kontakt zwischen Rolle und Seil besteht. Daher findest du bei Differenzialflaschenzügen üblicherweise Zahnräder und Ketten.
7.5.7 Herleitung Differenzialflaschenzug
Eine Möglichkeit, das Kräfteverhältnis beim Differenzialflaschenzug herzuleiten, besteht darin, die angreifenden Drehmomente zu betrachten (Bild 7.38).
Die lose Rolle teilt die Kraft \(F\) auf zwei gleich große Teilkräfte auf. Diese bewirken ein größeres nach rechts (oder im Uhrzeigersinn drehendes) Moment (blau) mit \(-R\cdot F/2\) und ein kleineres nach links (oder gegen den Uhrzeigersinn drehendes) Moment (grün) mit \(+r\cdot F/2\). Für ein Momentengleichgewicht benötigen wir ein weiteres linksdrehendes Moment (rot) mit \(+R\cdot F_\text{Z}\). Für das Gesamtdrehmoment gilt dann:
\[ M_\text{ges} = \textcolor{red}{R\cdot F_\text{Z}} + \textcolor{green}{r\cdot \frac{F}{2}} \textcolor{blue}{-R\cdot \frac{F}{2}} = 0 \]
Lösen wir diese Gleichung nach \(F_\text{Z}\), erhalten wir:
\[\begin{align} R\cdot F_\text{Z} + r\cdot \frac{F}{2} -R\cdot \frac{F}{2} = {} & 0 &&\qquad\Bigr\rvert +R\cdot \frac{F}{2} - r\cdot \frac{F}{2} \notag \\ R\cdot F_\text{Z} = {} & R\cdot \frac{F}{2} - r\cdot \frac{F}{2} &&\qquad\Bigr\rvert\;\text{(herausheben)} \notag \\ R\cdot F_\text{Z} = {} & (R - r)\cdot \frac{F}{2} &&\qquad\Bigr\rvert\cdot \frac{1}{R} \notag \\ F_\text{Z} = {} & \frac{R - r}{2R}\cdot F \notag \\ \end{align}\]
Damit erhalten wir für das Kräfteverhältnis beim Differentialflaschenzug die Gleichung (7.14).