5.2.1 Hubarbeit

Um einen Körper zu heben, musst du Arbeit gegen seine Gewichtskraft verrichten. Diese Arbeit wird Hubarbeit (engl. lifting work) genannt (Bild 5.8).

Bild 5.8: Arbeit gegen die Gewichtskraft

Setzen wir für die Kraft die Gewichtskraft \(F_G = m\cdot g\) und für den zurückgelegten Weg die Hubhöhe \(h\) in die allgemeine Formel für die Arbeit ein, erhältst du:

Die Formel geht davon aus, dass sich die Gewichtskraft entlang des Weges nicht ändert. Für kleine Hubhöhen – beispielsweise das Heben einer Kiste vom Boden auf einen Tisch – trifft das zu. Für große Hubhöhen wie zum Beispiel das „Heben“ eines Satelliten in die Erdumlaufbahn ist \(g\) nicht mehr konstant und es muss eine kompliziertere Formel für die Berechnung der Hubarbeit verwendet werden.

5.2.2 Hubarbeit entlang einer Rampe

Soll ein Lastwagen mit Fässern beladen werden, gibt es zwei Möglichkeiten:

1. Die Fässer direkt auf die Ladefläche heben.
2. Die Fässer (reibungsfrei) entlang einer Rampe hinauf rollen.

Betrachten wir beide Situationen genauer.

Bild 5.9: Hubarbeit entlang einer Rampe

Auf der rechten Seite von Bild 5.9 siehst du die Situation beim direkten Heben eines Körpers auf die Höhe \(h\). Der Weg ist \(s_2\) und die aufzubringende Kraft \(m\cdot g\). Darüber erkennst du die Hubarbeit als Fläche unter der Kurve im Kraft-Weg-Diagramm.

Auf der linken Seite von Bild 5.9 siehst du die Situation beim (reibungsfreien) Befördern eines Körpers über eine Rampe. In diesem Fall muss nur mehr ein Teil der Gewichtskraft, nämlich die Hangabtriebskraft, überwunden werden. Der Weg \(s_2\) über die Rampe ist allerdings wesentlich länger. Auch in diesem Fall erkennst du die Hubarbeit als Fläche unter der Kurve im Kraft-Weg-Diagramm darüber.

Beim Vergleich beider Flächeninhalte siehst du, dass die Arbeit in beiden Fällen immer dieselbe ist. Und das unabhängig davon, wie steil die Rampe ist. Das ist natürlich kein Zufall. In der Abbildung kannst du zwei ähnliche Dreiecke entdecken (gelb und türkisfarben) – wie du am gemeinsamen Winkel \(\alpha\) erkennst. Daher gilt für das Verhältnis der Dreiecksseiten (mit \(h = s_2\)):

\[ (\mathrm{gelbes\ \triangle})\quad s_1 : s_2 = F_G : F_\mathrm{HA} \quad(\mathrm{türkises\ \triangle}) \]

Durch Umformen erhältst du:

\[\begin{align} \frac{s_1}{s_2} = {} & \frac{F_G}{F_\mathrm{HA}} &&\qquad\Bigr\rvert\cdot s_2\cdot F_\mathrm{HA} \notag \\ s_1\cdot F_\mathrm{HA} = {} & s_2\cdot F_G \notag \\ \end{align}\]

Das Produkt auf beiden Seiten ist also unabhängig vom Neigungswinkel \(\alpha\) der schiefen Ebene immer gleich.

5.2.3 Goldene Regel der Mechanik

Verwendest du Werkzeuge, kannst du die Kraft für die Verrichtung einer Arbeit zwar verringern. Das verlängert aber auch immer entsprechend den Weg. Die verrichtete Arbeit bleibt dabei immer dieselbe. Diese Erkenntnis ist in der goldenen Regel der Mechanik (engl. The Golden Rule of Mechanics) zusammengefasst.

5.2.4 Beschleunigungsarbeit

Wie du beim dynamischen Grundgesetz gesehen hast, ist für das Beschleunigen eines Körpers immer eine Kraft notwendig. Die verrichtete Arbeit entlang der Beschleunigungsstrecke heißt Beschleunigungsarbeit. Dabei muss Arbeit gegen die Trägheit der Masse verrichten werden. Die Arbeit, um einen ruhenden Körper der Masse \(m\) auf eine bestimmte Endgeschwindigkeit \(v\) zu bringen, kann mit dieser Formel berechnet werden:

5.2.5 Herleitung Beschleunigungsarbeit

Für die Herleitung der Formel für die Beschleunigungsarbeit gehen wir von einer konstanten Beschleunigung aus. Für die Endgeschwindigkeit \(v\) und die Beschleunigungsstrecke \(s\) dürfen wir daher die Formeln der gleichmäßig beschleunigten Bewegung verwenden. Außerdem benötigen wir für die Herleitung noch die Definitionsgleichung der Kraft.

\[\begin{align} W_B = {} & F_s \cdot s &&\qquad\Bigr\rvert\; F=m \cdot a \notag \\ = {} & m \cdot a \cdot s &&\qquad\Bigr\rvert\; s=\frac{a\cdot t^2}{2} \notag \\ = {} & m \cdot a \cdot \frac{a\cdot t^2}{2} \notag \\ = {} & \frac{m}{2} \cdot a^2 \cdot t^2 \notag \\ = {} & \frac{m}{2} \cdot (a \cdot t)^2 &&\qquad\Bigr\rvert\; v=a\cdot t \notag \\ = {} & \frac{m}{2} \cdot v^2 \notag \\ \end{align}\]

Und wir erhalten:

\[ W_B = \frac{m \cdot v^2}{2} \]

Für die Herleitung sind wir von einer gleichmäßig beschleunigten Bewegung ausgegangen. Das Ergebnis gilt aber ganz allgemein, egal, ob der Körper gleichmäßig oder ungleichmäßig auf die Endgeschwindigkeit \(v\) beschleunigt wurde!

5.2.6 Elastische Verformungsarbeit

Das Dehnen oder Stauchen einer Schraubenfeder erfordert ebenfalls Arbeit. Die Arbeit gegen die Federkraft eines elastischen Körpers wird Spann- oder elastische Verformungsarbeit genannt. Du kannst sie mit der folgenden Formel berechnen:

Dabei ist \(x\) die Elongation (Längenänderung relativ zur entspannten Länge) und \(k\) die Federkonstante, die du schon aus dem Hookesche Gesetz kennst.

5.2.7 Herleitung elastische Verformungsarbeit

Für die Herleitung der elastischen Verformungsarbeit benötigen wir das Hookesche Gesetz, das die nötige Kraft zum Spannen (und Stauchen) einer Schraubenfeder beschreibt. Dabei fällt auf, dass im Gegensatz zur Hub- und Beschleunigungsarbeit, dass die Kraft beim Spannen einer Feder nicht konstant ist (Bild 5.10)!

Bild 5.10: Spannarbeit bei einer Schraubenfedern

Glücklicherweise steigt die Kraft beim Spannen einer Schraubenfeder linear an. Dadurch kannst du die Arbeit recht einfach über den Flächeninhalt im F-s-Diagramm berechnen – die Dreiecksfläche ist der halbe Flächeninhalt des Rechtecks mit den Seiten \(k\cdot x\) und \(x\).

\[ W_S = \frac{(k\cdot x)\cdot x}{2} = \frac{k\cdot x^2}{2} \]

5.2.8 Muskelarbeit

Ein Kran, der eine Masse auf einer bestimmten Höhe hält, verrichtet keine Arbeit. Es wirkt zwar eine Kraft (Schwerkraft), aber der zurückgelegte Weg ist null und somit ist auch das Produkt aus Kraft und Weg null (Bild 5.11, links).

Bild 5.11: Halten einer Last bei Maschine und Mensch

Hältst du einen Rucksack am ausgestreckten Arm, sollte also ebenfalls keine Arbeit verrichtet werden (Bild 5.11, rechts). Aus deiner Erfahrung weißt du aber, dass das Halten eines Körpers auf gleicher Höhe für dich mit Anstrengung verbunden ist. Nach einiger Zeit fängt dein Arm an zu zittern und irgendwann musst du den Arm senken. Gilt für Lebewesen die Definition der mechanischen Arbeit nicht? Es ist zwar richtig, dass die mechanische Arbeit eingeführt wurde, um die Arbeit von Maschinen zu beschreiben, aber sie trifft auch auf Lebewesen zu. Um zu verstehen, warum das Halten eines Körpers für ein Lebewesen mit Arbeit verbunden ist, müssen wir uns ansehen, wie ein Muskel eigentlich funktioniert.

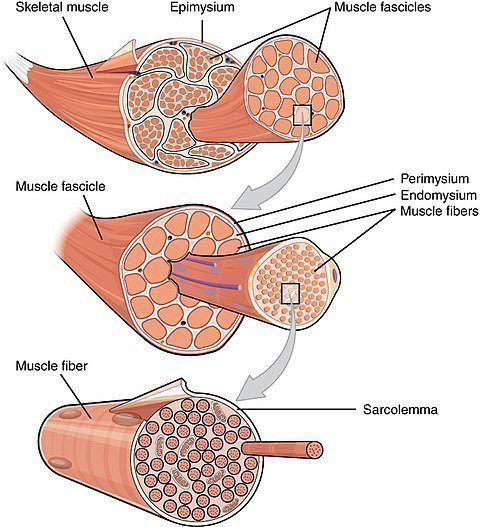
Muskelkraft beruht auf der Muskelverkürzung und du verwendest sie entweder direkt – etwa beim Gehen – oder in Muskelkraftmaschinen wie zum Beispiel deinem Fahrrad. In Bild 5.12 siehst du den Aufbau eines Muskels: Jeder Muskel bestehst aus Muskelfaserbündel (oben) zu denen die einzelnen Muskelfasern (Mitte) zusammengefasst sind. Jede Muskelfaser besteht aus bis zu mehreren Hundert Muskelfibrillen (Myofibrillen) von je einem Durchmesser von etwa \(1\;\mathrm{\mu m}\) (unten). Diese Muskelfibrillen schieben sich beim Anspannen eines Muskels teleskopartig ineinander und sorgen für die Verkürzung.

Bild 5.12: Aufbau eines Muskels

Die in den Muskelfibrillen enthaltenen Myosinfilamente (gelb) besitzen winzige „Köpfchen“ (Bild 5.13). Durch eine chemische Reaktion docken diese an einem benachbarten Aktin-Protein des Filaments (rosa) an, kippen um etwa \(45^\circ\) und ziehen sich um ein kleines Stück weiter. Danach entkoppeln sich die Proteine wieder. Das passiert sehr schnell, sodass sich dieser Zyklus (Querbrückenzyklus) bis zu 50 Mal in der Sekunde wiederholen kann. Auf diese Weise kann sich die Länge eines Muskels in deutlich weniger als einer Sekunde auf bis zu \(50\,\%\) verkürzen!

Bild 5.13: Querbrückenzyklus einer Muskelkontraktion

Beim Anspannen eines Muskels ist also auf mikroskopischer Ebene ständig eine Bewegung vorhanden und damit verrichtet dein Muskel selbst beim Halten eines Gegenstandes ständig physikalische Arbeit!

Nicht alle Muskelfasern innerhalb eines Muskels ziehen sich gleichzeitig zusammen. Stattdessen wird die Arbeit auf unterschiedliche Fasern verteilen. Während einige Fasern arbeiten, ruhen sich andere gerade aus. Die für den Querbrückenzyklus notwendige Energie wird aus dem in den Zellen gespeicherten Energieträger Adenosin-Triphosphat (ATP) gewonnen, indem ein Phosphat von dem Molekül abgespalten wird. Bei langer Anspannung gehen die ATP Vorräte im Muskel zu Ende und nicht mehr alle benötigen Muskelfaser können kontrahieren. Das äußert sich dann in einem Muskelzittern, bei dem die Bewegung dann plötzlich sichtbar wird.