14.11 Kinetische Gastheorie
Bisher haben wir ein Gas immer makroskopisch behandelt und uns Druck, Temperatur und Volumen angesehen. Außerdem haben wir schon mehrmals erwähnt, dass es einen Zusammenhang zwischen innerer Energie und Temperatur gibt. In diesem Kapitel werden wir uns mit den mikroskopischen Eigenschaften der Gasteilchen (Masse und kinetische Energie) beschäftigen und ihren Zusammenhang mit den makroskopischen Größen zeigen.
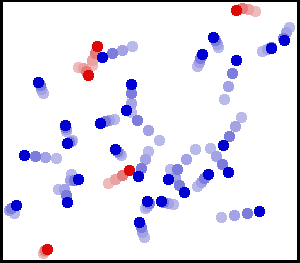
In Bild 14.70 siehst du das Modell eines Gases. Die Gasteilchen bewegen sich in zufällige Richtungen und mit unterschiedlichen Geschwindigkeiten. Bei jedem Stoß ändern sich ihre Richtungen und Geschwindigkeiten. Die Farbe der Gasteilchen in dem Bild hat keine Bedeutung und soll dir nur helfen, der Bewegung einzelner Gasteilchen zu verfolgen.
In einem Liter Luft bei Normalbedingungen befinden sich rund \(10^{22}\)(!) Luftteilchen. Daher können wir nicht mehr nur mit einzelnen Teilchen rechnen, sondern müssen die Statistik zu Hilfe nehmen. Das Teilgebiet der Mechanik, das physikalische Größen einer großen Anzahl von Teilchen mit statistischen Mitteln beschreibt, heißt statistische Mechanik.
Alle folgenden Überlegungen und Formeln gelten für die Annahme eines idealen Gases.
14.11.1 Mittlere kinetische Energie und Druck
Stell dir ein Gas in einem geschlossenen Volumen vor (Bild 14.70). Jedes Mal, wenn ein Gasteilchen auf eine Wand trifft, wird es reflektiert und übt eine Kraft auf die Wand aus. Da ein Gas aus so vielen und so kleinen Teilchen besteht, können wir eine einzelne Kollision makroskopisch nicht beobachten. Die Summe all dieser Kollisionen bemerken wir als kontinuierlichen Druck auf die Gefäßwände.
Gehen wir von einem einatomigen Gas aus (alle Gasteilchen sind gleich), dann lautet der Zusammenhang:
| \[\begin{equation} p = \frac{2}{3}\cdot\frac{N}{V}\cdot\left(\frac{m\cdot\overline{v^2}}{2}\right) \tag{14.16} \end{equation}\] |
In dieser Gleichung steht:
- \(p\), den makroskopisch messbaren Druck (Einheit \(\mathrm{Pa}\))
- \(V\), das makroskopisch messbare Volumen (Einheit \(\mathrm{m}^3\))
- \(N\), die Anzahl der Gasteilchen in dem Volumen (in Stück, also eine dimensionslose Größe)
- \(m\) die Masse eines Gasteilchens (Einheit \(\mathrm{kg}\))
- \(\overline{v^2}\), das mittlere Geschwindigkeitsquadrat der Teilchen (Einheit \(\mathrm{m}^2/\mathrm{s}^2\))
Vielleicht wunderst du dich, dass in der Formel nicht gekürzt wurde. Das ist Absicht, denn so kannst du den Ausdruck für die mittlere kinetische Energie der Gasteilchen in der Formel erkennen.
Beachte: Die Ausdrücke \(\overline{v^2}\) und \(\overline{v}^2\) sind nicht dasselbe!
Die Herleitung für diesen Zusammenhang findest du weiter unten in diesem Kapitel.
14.11.2 Mittleres Geschwindigkeitsquadrat
Die Ausdrücke \(\overline{v^2}\) (also das mittlere Geschwindigkeitsquadrat, engl. average squared speed) und \(\overline{v}^2\) (also die zweite Potenz der mittleren Geschwindigkeit) sind nicht dasselbe!
Ein einfaches Zahlenbeispiel soll dir den Unterschied zeigen. Nehmen wir die Zahlenmenge \(\{1, 2, 3, 4\}\).
Bildest du davon den Mittelwert (\(\overline{v}=2{,}5\)) und anschließend das Quadrat, erhältst du das Quadrat der mittleren Geschwindigkeit: \(\overline{v}^2=6{,}25\)
Bildest du zuerst die Quadrate (\(\{1, 4, 9, 16\}\)) und bildest davon den Mittelwert, erhältst du das mittlere Geschwindigkeitsquadrat: \(\overline{v^2}=7{,}5\)
Wie du an den Ergebnissen sehen kannst, liefern beide Ausdrücke im Allgemeinen nicht denselben Wert!
14.11.3 Mittlere kinetische Energie und Temperatur
Mit dem Zusammenhang von mittlerer kinetische Energie der Gasteilchen und dem makroskopischen Druck können wir einen Zusammenhang zwischen absoluter Temperatur \(T\) und der mittleren kinetischen Energie der Teilchen herstellen.
\[ \begin{aligned} p = {} & \frac{2}{3}\cdot\frac{N}{V}\cdot\left(\frac{m\cdot\overline{v^2}}{2}\right) \qquad\Bigr\rvert\cdot V\\ p\cdot V = {} & \frac{2}{3}\cdot N\cdot\left(\frac{m\cdot\overline{v^2}}{2}\right) \\ \end{aligned} \]
Für \(p\cdot V\) setzen wir das ideale Gasgesetz in der Form \(p\cdot V=N\cdot k\cdot T\) ein und du erhältst den Zusammenhang:
| \[\begin{equation} T = \frac{2}{3\cdot k}\cdot\left(\frac{m\cdot\overline{v^2}}{2}\right) \tag{14.17} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(T\), die absolute Temperatur (Einheit \(\mathrm{K}\))
- \(k\), die Boltzmann-Konstante (\(1{,}4\cdot 10^{-23}\;\frac{\mathrm{J}}{\mathrm{K}}\))
- \(m\), die Masse eines Gasteilchens (Einheit \(\mathrm{kg}\))
- \(\overline{v^2}\), das mittlere Geschwindigkeitsquadrat der Teilchen (Einheit \(\mathrm{m}^2/\mathrm{s}^2\))
| Die absolute Temperatur ist ein Maß für die durchschnittliche kinetische Energie der zufälligen translatorischen (geradlinigen) Bewegung der Moleküle in einem Gas. |
Wie bei der Formel für den Druck gilt auch hier: In der Formel wurde absichtlich nicht gekürzt, damit du die Formel für die mittlere kinetische Energie der Gasteilchen in der Formel erkennen kannst.
Beachte: Die Ausdrücke \(\overline{v^2}\) und \(\overline{v}^2\) sind nicht dasselbe!
14.11.4 Temperatur und innere Energie
Bisher wurde schon mehrmals erwähnt, dass die absolute Temperatur ein Maß für die innere Energie ist. Für ideale Gase lässt sich der Zusammenhang konkret zeigen. Die innere Energie ist die Summe aller Bewegungsenergien. Bei \(N\) Gasteilchen, die jeweils eine mittlere kinetische Energie von \(m\cdot\overline{v^2}/2\) haben, ergibt sich für die innere Energie \(U\) eines Gases der Ausdruck:
\[ U = N\cdot \left(\frac{m\cdot\overline{v^2}}{2}\right) \]
Aus dem Zusammenhang zwischen mittlerer kinetischer Energie und Temperatur erhalten wir einen Ausdruck für die mittlere kinetische Energie:
\[ \begin{aligned} T = {} & \frac{2}{3\cdot k}\cdot\left(\frac{m\cdot\overline{v^2}}{2}\right)\qquad\Bigr\rvert\cdot \frac{3\cdot k}{2}\\ \frac{3}{2}\cdot k\cdot T = {} & \left(\frac{m\cdot\overline{v^2}}{2}\right)\\ \end{aligned} \]
Setzt du diesen Ausdruck in die Formel für die innere Energie ein, erhältst du:
| \[\begin{equation} U = \frac{3}{2}\cdot N\cdot k\cdot T \tag{14.18} \end{equation}\] |
In dieser Gleichung bedeuten:
- \(U\), die Innere Energie (Einheit \(\mathrm{J}\))
- \(N\), die Anzahl der Gasteilchen in dem Volumen (in Stück, also eine dimensionslose Größe)
- \(k\), die Boltzmann-Konstante (\(1{,}4\cdot 10^{-23}\;\frac{\mathrm{J}}{\mathrm{K}}\))
- \(T\), die absolute Temperatur (Einheit \(\mathrm{K}\))
Du siehst also:
| Die absolute Temperatur ist direkt proportional zur inneren Energie eines Gases. |
14.11.5 Molekülgeschwindigkeit in einem idealen Gas
Wie groß ist die Geschwindigkeit eines Gasteilchens, das eine mittlere kinetische Energie von \(m\cdot\overline{v^2}/2\) besitzt? Der Zusammenhang zwischen Temperatur und Innerer Energie in einem Gas liefert uns eine Antwort auf diese Frage.
\[\begin{equation} \begin{aligned} U = \left(\frac{m\cdot\overline{v^2}}{2}\right)\cdot N = {} & \frac{3}{2}\cdot N\cdot k\cdot T &&\Bigr\rvert\cdot \frac{1}{N} \\ \frac{m\cdot\overline{v^2}}{2} = {} & \frac{3}{2}\cdot k\cdot T &&\Bigr\rvert\cdot \frac{2}{m} \\ \overline{v^2} = {} & \frac{3\cdot k\cdot T}{m} &&\Bigr\rvert \sqrt{(\ldots)} \\ \sqrt{\overline{v^2}} = {} & \sqrt{\frac{3\cdot k\cdot T}{m}} = v_{rms}\\ \end{aligned} \tag{14.19} \end{equation}\]
Dieser Wert hat die Dimension einer Geschwindigkeit. Diese Abschätzung für die Molekülgeschwindigkeit in einem Gas wird als quadratisch gemittelte Geschwindigkeit \(v_{rms}\) (engl. thermal speed) bezeichnet (die Abkürzung kommt von root mean square – der englischen Bezeichnung für das quadratische Mittel).
Vorsicht: die quadratisch gemittelte Geschwindigkeit \(\sqrt{\overline{v^2}}\) unterscheidet sich von der mittleren Geschwindigkeit \(\overline{v}\) in einem Gas!
Aus der Gleichung kannst du erkennen:
Je größer die Temperatur, desto größer die Geschwindigkeit
Je kleiner die Masse der Moleküle, desto größer die Geschwindigkeit (bei gleicher Temperatur)
In der Wikipedia findest du konkrete Werte für die quadratisch gemittelte Geschwindigkeit einiger realen Gase bei Raumtemperatur. Die quadratisch gemittelte Geschwindigkeit von Luft bei \(20\;^\circ\mathrm{C}\) (\(293{,}15\;\mathrm{K}\)) liegt, ist \(v_{rms}=464\;\mathrm{m/s}\). Vergleichst du das Ergebnis mit der Animation 14.70 am Anfang des Kapitels, wirst du feststellen, dass diese stark untertrieben sind. Die Geschwindigkeiten in einem Gas sind rund \(10{.}000\) Mal schneller als in der Animation dargestellt!
Die Geschwindigkeit der Gasteilchen ist entscheidend für die Weitergabe von Information durch Stöße. Daher wird es dich nicht wundern, diese Geschwindigkeit in der Größenordnung der Schallgeschwindigkeit in Luft bei Raumtemperatur von rund \(340\;\mathrm{m/s}\) liegt. Die quadratisch gemittelte Geschwindigkeit liefert eine ungefähre Obergrenze für die maximale Geschwindigkeit, mit der Informationen durch Druckschwankungen übertragen werden können – in unserem Fall durch Schall in Luft.
14.11.6 Geschwindigkeitsverteilung in einem idealen Gas
In allen Abschnitten dieses Kapitels haben wir immer nur Aussagen über durchschnittliche Werte erhalten. So liefert uns die Formel für die quadratisch gemittelte Geschwindigkeit zum Beispiel einen Eindruck davon, wie schnell sich Moleküle in einem Gas ungefähr bewegen. Aber sind die Geschwindigkeiten aller Gasmoleküle fast gleich groß oder über einen weiten Geschwindigkeit-Bereich verteilt?
Die Antwort darauf gibt uns die nach James Clerk Maxwell und Ludwig Boltzmann benannte Maxwell-Boltzmann Verteilung (engl. Maxwell-Boltzmann distribution) für die Molekülgeschwindigkeit in einem Gas. In Bild 14.71 siehst du die konkreten Verteilungen für unterschiedliche Temperaturen.
Im Gegensatz zu anderen Verteilungsfunktionen (wie etwa der Normalverteilung), ist die Verteilung der Molekülgeschwindigkeiten nicht symmetrisch. Während die kleinste mögliche Geschwindigkeit null ist (also nach unten begrenzt ist), kann die Geschwindigkeit beliebig groß werden. Diese Asymmetrie in der Verteilungskurve bewirkt, dass die häufigste vorkommende Geschwindigkeit in einem Gas (beim Maximum der Verteilungskurve, Punkt 1) immer kleiner als die durchschnittliche Molekülgeschwindigkeit \(\overline{v}\) (Punkt 2) ist. Punkt 3 in Bild 14.71 zeigt die Lage der quadratisch gemittelten Geschwindigkeit \(v_{rms}\).
Steigt die Temperatur, wird die Kurve immer breiter und niedriger. Die Geschwindigkeit der Gasteilchen verteilt sich auf einen immer größeren Geschwindigkeitsbereich, aber die Anzahl der Teilchen bleibt unverändert. Daher ist der Flächeninhalt unter allen Kurven eines Gases immer gleich groß.
14.11.7 Herleitung Zusammenhang von mittlerer kinetischer Energie und Druck
Für die Herleitung nehmen wir an, dass sich \(N\) gleiche Gasteilchen mit der Masse \(m\) in einem quaderförmigen Gasbehälter mit konstantem Volumen befinden.
Wir werden die Herleitung in vier Schritten führen:
- Kraftstoß eines Moleküls auf eine Wand
- Gesamtenergie des Gases
- Mittleren kinetische Energie eines Teilchens
- Zusammenfassung
Schritt 1
Zunächst betrachten wir nur ein einziges Molekül, das sich mit der Geschwindigkeit \(v\) in der x-Richtung bewegt (Bild 14.72).
Das Teilchen trifft die Wand \(A\) und führt einen vollkommen elastischen Stoß aus. Der Impuls vor dem Stoß ist \(p=m\cdot v\) und nach dem Stoß \(p^\prime=-m\cdot v\) (Bild 14.73).
Für die Impulsänderung des Teilchens erhältst du den Wert:
\[ \Delta p = p^\prime - p = -m\cdot v - m\cdot v = -2\cdot m\cdot v \]
Die Wand \(A\) erfährt einen gegengleichen Kraftstoß \(\Delta p = 2\cdot m\cdot v\).
Trifft ein Molekül auf die Wand, übt es nur kurzfristig eine Kraft auf diese Wand aus. Erst wenn das Molekül an der gegenüberliegenden Wand reflektiert wurde, kehrt es zu Wand \(A\) zurück und übt erneut kurzfristig eine Kraft auf diese Wand aus (Bild 14.74, oben).
Für eine gleichwertige konstante Kraft \(F\) die auf die Wand \(A\) ständig wirkt (Bild 14.74, unten) gilt:
\[ F = \frac{\Delta p}{\Delta t} = \frac{2\cdot m\cdot v}{\Delta t} \]
Wobei die Zeit \(\Delta t\) die Zeit zwischen zwei aufeinander folgender Stöße mit derselben Wand ist. Der Weg, den das Teilchen in dieser Zeit zurücklegen muss, ist \(s=2a\) (hin und zurück in Bild 14.72).
Gehen wir von einer konstanten Geschwindigkeit \(v\) aus, erhältst du für die Zeit zwischen zwei aufeinander folgenden Stößen mit der Wand \(A\):
\[ \Delta t = \frac{2\cdot a}{v} \]
Und für die Kraft gilt:
\[ F = \frac{2\cdot m\cdot v}{\Delta t} = \frac{2\cdot m\cdot v}{\frac{2\cdot a}{v}} = \frac{m\cdot v^2}{a} \]
Der Druck \(p\) ist definiert als Kraft pro Fläche (Vorsicht: \(p\) steht hier für den Druck, nicht den Impuls!). Für den mittleren Druck \(p_1\) eines Teilchens (daher verwenden wir den Index 1) auf die Seitenfläche \(A\) gilt:
\[ p_1 = \frac{F}{A} = \frac{m\cdot v^2}{A\cdot a} = \frac{m\cdot v^2}{V} = \frac{2}{V}\cdot\frac{m\cdot v^2}{2} = \frac{2}{V}\cdot E_{kin,x} \]
Durch das Erweitern des Bruches durch die Zahl Zwei können wir die kinetische Energie des Teilchens in dem Ausdruck erkennen. Die Bewegungsenergie bestimmt also den Druck.
Schritt 2
Die \(N\) Gasteilchen, die sich insgesamt in dem Gasvolumen befinden, bewegen sich mit unterschiedlichen Geschwindigkeiten und in unterschiedliche Richtungen. Aber: Da im Gleichgewichtszustand der makroskopische Druck konstant ist, muss die Summe der kinetischen Energien \(E_{\text{KIN},ges}\) aller Teilchen konstant sein. Ordnen wir jedem Molekül die mittlere Bewegungsenergie von
\[ \overline{E}_{\text{KIN}} = \frac{m\cdot\overline{v^2}}{2} \]
zu, gilt für die Gesamtbewegungsenergie:
\[ E_{\text{KIN},ges} = N\cdot \overline{E}_{\text{KIN}} \]
Schritt 3
Die mittlere kinetische Energie eines Teilchens lässt sich als die Summe der mittleren kinetischen Energien seiner Geschwindigkeits-Komponenten schreiben:
\[ \overline{E}_{\text{KIN}} = \overline{E}_{\text{KIN},x} + \overline{E}_{\text{KIN},y} + \overline{E}_{\text{KIN},z} \]
Wenn wir davon ausgehen, dass keine Bewegungsrichtung im Gas ausgezeichnet ist (ein solches Gas heißt isotrop), sind die mittleren kinetischen Energien der einzelnen Geschwindigkeits-Komponenten alle gleich groß und es gilt:
\[ \overline{E}_{\text{KIN},x} = \overline{E}_{\text{KIN},y} = \overline{E}_{\text{KIN},z} \]
Und wir können die mittleren kinetischen Energien in x-Richtung als Teil der gesamten kinetischen Energie eines Teilchens ausdrücken:
\[ \overline{E}_{\text{KIN},x} = \frac{1}{3}\cdot \overline{E}_{\text{KIN}} \]
Schritt 4
Zum Schluss setzen wir alle Schritte zusammen. Den mittleren Druck für ein Teilchen aus Schritt 1 können wir jetzt so ausdrücken:
\[ p_1 = \frac{2}{V}\cdot \frac{1}{3}\cdot \overline{E}_{\text{KIN}} = \frac{2}{3}\cdot \frac{1}{V}\cdot \overline{E}_{\text{KIN}} \]
Und der Druck für alle \(N\) Teilchen:
\[ p = \frac{2}{3}\cdot \frac{1}{V}\cdot N\cdot \overline{E}_{\text{KIN}} = \frac{2}{3}\cdot \frac{N}{V}\cdot \frac{m\cdot\overline{v^2}}{2} \]
Und wir erhalten die gesuchte Beziehung.
Aber haben wir nicht die anderen Seitenflächen vergessen? Berücksichtigen wir alle sechs Seitenflächen, erhalten wir zwar die sechsfache Kraft, aber die verteilt sich auch auf eine sechsfach so große Fläche und damit erhältst du wieder denselben Druck.