16.1 Lichtgeschwindigkeit
In Bild 16.2 siehst du einen Laserstrahl. Er breitet sich mit Lichtgeschwindigkeit aus, so wie jede elektromagnetische Welle.
Licht hat eine unglaublich große Geschwindigkeit von rund \(c_0 = 3\cdot 10^{8}\;\mathrm{m/s}\) (dreihundert Millionen) im Vakuum (exakt \(299\,792\,458\;\mathrm{m/s}\)). Die Lichtgeschwindigkeit ist nicht nur unglaublich schnell, die intensive Beschäftigung mit ihr hat auch zu einem neuen Zweig der Physik geführt.
In diesem Kapitel geht es um die Messung der Lichtgeschwindigkeit, die Frage, in welchem Medium sich elektromagnetische Wellen ausbreiten und was eigentlich „messen“ genau bedeutet.
Links:
16.1.1 Astronomische Aberration
Beobachtest du einen Stern in Richtung des Ekliptik-Pols, scheint dieser sich im Laufe eines Jahres entlang eines Kreises zu bewegen. Diese Abweichung von der tatsächlichen Sternposition wird astronomische Aberration (engl. astronomical aberration, von dem lateinischen Wort aberratio für „Ablenkung“) genannt. Die Ursache dafür ist die Bewegung der Erde um die Sonne (Bild 16.3).
Stell dir eine Person im Regen vor (Bild 16.4). Steht die Person still und fällt der Regen senkrecht, wird sie bei einem gerade gehaltenen Regenschirm am wenigsten nass (a). Sobald die Person läuft, muss sie auch die Neigung des Regenschirms anpassen, um so wenig wie möglich nass zu werden (b). Aus der Sicht des Läufers kommen ihm die Regentropfen entgegen (c). Das letzte Bild entspricht dem Erdbeobachter. Der Regen entspricht den Lichtteilchen und die Neigung des Schirms der Neigung des Fernrohres.
Der Winkel der Aberration hängt sowohl von der Geschwindigkeit der Erde um die Sonne \(v\) als auch von der Lichtgeschwindigkeit \(c\) ab. James Bradley nutzte diesen Zusammenhang Anfang des 18. Jahrhunderts, um die Größe der Lichtgeschwindigkeit abzuschätzen. Da winzige Fehler in der Winkelmessung zu großen Fehlern in der Berechnung der Geschwindigkeit führen, war die Abschätzung nur sehr ungenau. Aber alleine die Tatsache, dass es zu einer Aberration kommt, zeigt, dass die Lichtgeschwindigkeit endlich sein muss.
16.1.2 Messung der Lichtgeschwindigkeit nach Foucault
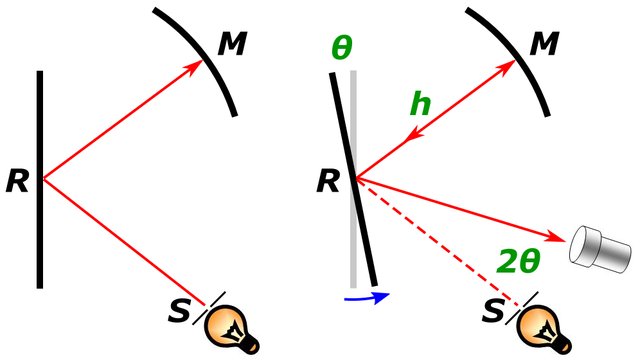
Mitte des 19. Jahrhunderts baute Léon Foucault die Anordnung in Bild 16.5 zur Bestimmung der Lichtgeschwindigkeit.
Bei dieser Apparatur trifft ein Lichtpuls durch Spalt \(S\) auf einen rotierenden Spiegel \(R\) und reflektiert ihn auf einen fixen Spiegel \(M\). Dort wird der Lichtpuls zurück reflektiert. Hat sich der Spiegel \(R\) zwischen den beiden Reflexionen um den Winkel \(\theta\) gedreht, trifft der Lichtpuls um den Winkel \(2\cdot\theta\) abgelenkt auf den Detektor.
Bezeichnen wir den Abstand zwischen den Spiegeln mit \(h\), beträgt die Zeit \(t\) zwischen der ersten und zweiten Reflexion am rotierenden Spiegel \(2h/c\), wobei \(c\) die Lichtgeschwindigkeit bezeichnet. Wenn sich der Spiegel mit der konstanten Winkelgeschwindigkeit \(\omega\) dreht, überstreicht er in der Zeit \(t\) den Winkel \(\theta =\omega\cdot t\). Einsetzen liefert
\[ \theta =\omega\cdot t = \omega\cdot\left(\frac{2h}{c}\right) \]
Durch Umformen erhältst du
\[ \begin{aligned} \theta = {} & \omega\cdot\frac{2h}{c} &&\Bigr\rvert\cdot \frac{c}{\theta} \\ c = {} & \omega\cdot\frac{2h}{\theta} \\ \end{aligned} \]
Mit einem Abstand von \(h=20\;\mathrm{m}\) zwischen den Spiegeln, erhielt er den Wert \(298{.}000\;\mathrm{km/s}\) für die Lichtgeschwindigkeit – einen sehr exakten Wert, der nur etwa \(0{,}6\,\%\) vom aktuellen Wert abweicht!
16.1.3 Beobachten, nicht nur sehen
Die Lichtgeschwindigkeit ist zwar endlich, aber extrem groß. Die Lichtlaufzeit – die Zeit vom Aussenden des Lichts bis zum Eintreffen auf unserer Netzhaut – spielt bei unserer Wahrnehmung im Alltag keine Rolle. Wenn du den Lichtschalter betätigst, wird es „sofort“ hell. Wie würdest du die Welt sehen, wenn die Lichtlaufzeit vergleichbar mit der Bewegungsgeschwindigkeit von Objekten ist?
In Bild 16.6 siehst du ein Beispiel. Ein Würfel bewegt sich auf einer Schienenbahn von links nach rechts. Links siehst du deine Wahrnehmung des Würfels für kleine Geschwindigkeiten. Rechts unten siehst du deine Wahrnehmung, wenn er sich mit \(v=0{,}6\cdot c\) an dir vorbeibewegt – er erscheint verdreht und verzerrt. Der wesentliche Punkt ist, dass die Kanten des Würfels zu allen Zeiten gerade sind, die Deformation ist eine Folge der endlichen Lichtlaufzeit!
Bei extrem großen Geschwindigkeiten dürfen wir uns nicht mehr auf unser Sehen verlassen. Für unsere „Beobachtung“ müssen wir ein besseres System verwenden, um Effekte, die durch die endliche Lichtlaufzeit entstehen, auszuschließen. Für unsere zukünftigen Überlegungen stellen wir uns ein Koordinatengitter mit synchronisierten Uhren (Bild 16.7). Vor jeder Uhr steht eine Person. Erreicht ein Objekt den Ort der Person, notiert diese die Uhrzeit. Am Ende des Experiments treffen sich alle Personen und vergleichen ihre Aufzeichnungen.
16.1.4 Die Suche nach dem Ätherwind
Wasserwellen bewegen sich im Medium Wasser, Schallwellen bewegen sich im Medium Luft, aber in welchem Medium bewegt sich eine Lichtwelle? Dieses Medium, in dem sich Licht ausbreiten sollte, wurde Lichtäther (engl. aether) genannt. Ein Flugzeug kann die Geschwindigkeit zum umgebenden Medium Luft – den Fahrtwind (engl. airspeed) – zum Beispiel mithilfe eines Pitot-Rohres messen. Da das Licht weit entfernter Sterne auf der Erde zu sehen ist, muss das Weltall mit Lichtäther erfüllt sein. Daher sollte es auch möglich sein, die Bewegung der Erde relativ zum Lichtäther, den sogenannten Ätherwind (engl. aether wind) zu messen. Da die Bahngeschwindigkeit der Erde um die Sonne mit \(v=29\,780\;\mathrm{m}/\mathrm{s}\) relativ groß ist, sollte sich unsere Bewegung durchs All bei Signal-Übertragungen zu unterschiedlichen Tageszeiten bemerkbar machen (Bild 16.8).
In der Konstellation (a) sendet die Station 1 der Station 2 zu Mittag eine Nachricht. Da Station 2 dem Signal entgegenkommt, sollte sich die Signallaufzeit verkürzen. Die errechnete Signalgeschwindigkeit sollte \(c+v\) ergeben. Einen halben Tag später, um Mitternacht, erhalten wir Konstellation (b). Wieder sendet Station 1 an die Station 2 eine Nachricht. Dieses Mal sollte sich die Signallaufzeit aber vergrößern, da das Signal der sich entfernenden Empfangsstation 2 hinterher eilen muss. In diesem Fall sollte die berechnete Signalgeschwindigkeit nur \(c-v\) betragen.
Anfang des 20. Jahrhunderts wurde diese Abweichung mit dem Michelson-Morley-Experiment sehr genau untersucht. Alle Experimente ergaben dasselbe Ergebnis: Es ist keine Abweichung feststellbar. Die Lichtgeschwindigkeit beträgt zu allen Zeiten und in alle Richtungen immer genau \(c\).
16.1.5 Uhrensynchronisation
Das vorgestellte Verfahren zur korrekten Beobachtung setzt voraus, dass alle Uhren im System synchronisiert sind, also alle dieselbe Zeit anzeigen.
Du wirst jetzt sagen, dass dies eine einfache Aufgabe ist. Bevor eine Person auf ihren Beobachtungspunkt geht, synchronisiert sie ihre Uhr mit der ihres Nachbarn am selben Ort. Wir wollen aber ausschließen, dass selbst die Bewegung der Person zu ihrem Beobachtungspunkt schon den Gang der Uhr verändert.
Mit der Konstanz der Lichtgeschwindigkeit können wir folgendes Verfahren zur Uhrensynchronisation verwenden: Die Person im Koordinaten-Ursprung sendet beim Start ihrer Uhr einen kugelförmigen Lichtblitz in alle Richtungen aus. Jede Person kennt ihren Abstand vom Ursprung. Wird die Uhr bei einer anderen Station durch den Lichtblitz gestartet, stellt die Person die Uhr um die Dauer der (errechneten) Lichtlaufzeit nach vor, da sie ja zu einem späteren Zeitpunkt gestartet wurde als die Uhr im Ursprung. Auf diese Weise erhalten wir ein System aus lauter synchronisierten Uhren.
16.1.6 Zeitsynchronisation bei Funkuhren
Funkuhren verwenden das in Abschnitt Uhrensynchronisation beschriebene Verfahren. In Mitteleuropa sendet ein Zeitzeichensender in Mainflingen (Deutschland) ein Funksignal aus. Es enthält in binärer Form die aktuelle Uhrzeit und Datum (sowie Informationen zu Sommer/Winterzeit und Schaltsekunden). Die Funkuhr empfängt das Signal und passt die eigene Uhrzeit an diese Zeit-Informationen an.
Die Zeit-Information des Senders ist zwar auf eine Nanosekunde (eine milliardstel Sekunde) genau, einfache Funkwecker berücksichtigen aber die Signallaufzeit nicht. Nehmen wir an, dein Funkwecker steht in Wien. Die Entfernung Wien-Mainflingen (Luftlinie) beträgt \(571{,}7\;\mathrm{km}\) (Bild 16.9). Für die Signallaufzeit erhältst du
\[ t=\frac{s}{v}=\frac{571\,700\;\mathrm{m}}{3\cdot 10^{8}\;\mathrm{m/s}} = 0{,}0019\ldots\;\mathrm{s} \]
Dein Funkwecker geht also immer um rund \(1{,}90\ldots\) Millisekunden nach. Diese Abweichung ist für die meisten privaten Zwecke unbedeutend. In Forschungslabors wird diese Abweichung berücksichtigt.
Neben Zeitzeichensendern gibt es heute noch viele weitere Methoden, um eine sehr exakte Uhrzeit zu erhalten. Zum Beispiel senden alle Mobilfunkmasten ein Zeitsignal, mit dem Smartphones ihre Uhrzeit korrigieren. GPS fähige Geräte erhalten nicht nur Standortdaten, sondern auch eine Zeit-Information. Rundfunksender senden mit RDS/DAB parallel zum Programm ein Zeitsignal, das (Auto-)Radios auswerten.
