3.4 Bewegungsdiagramme
In Bild 3.20 siehst du eine Tachoscheibe (engl. tachograph disk), wie sie in mechanischen Fahrtenschreibern verwendet wurde. Mit ihrer Hilfe wurde früher die Bewegung von Fahrzeugen aufgezeichnet. Die Kurve zeigt die Geschwindigkeit (eigentlich Tempo) eines Fahrzeuges zu einer bestimmten Zeit.
Auch wenn heute die Aufzeichnung der Bewegung von Fahrzeugen elektronisch erfolgt, sind die aufgezeichneten Kurven immer noch dieselben. Um die unterschiedlichen Bewegungskurven, deren Interpretation und Zusammenhang geht es in diesem Kapitel.
In diesem Kapitel beschränken wir uns auf eindimensionale Bewegungen, also zum Beispiel ein Fahrzeug, das auf einer geraden Straße vor- und zurückfahren kann.
3.4.1 Ort-Zeit-Diagramm
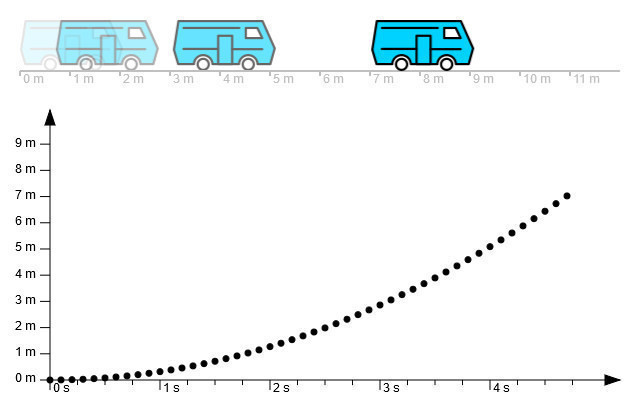
Eine eindimensionale Bewegung wird oft in einem Ort-Zeit-Diagramm (engl. displacement-time graph oder position-time graph) zusammengefasst. Die Zeit wird immer auf der waagrechten Achse aufgetragen. Der Ort, an dem sich der Körper zu dem jeweiligen Zeitpunkt befindet, wird auf der senkrechten Achse aufgetragen. Im Bild 3.21 entspricht der eingezeichnete Ort dem Heck des Fahrzeugs.
In Bild oben siehst du das Ort-Zeit-Diagramm eines Fahrzeugs. Über einen Zeitraum von 7 Sekunden wurde in regelmäßigen Zeitabständen der aktuelle Ort des Hecks des Fahrzeugs gemessen und im Diagramm eingezeichnet.
3.4.2 Mittlere Geschwindigkeit im Ort-Zeit-Diagramm
Betrachten wir jetzt zwei Punkte im Ort-Zeit-Diagramm (Bild 3.22) zu den Zeitpunkten \(t_1\) und \(t_2\).
Die Größen \(t_2-t_1\) und \(s_2-s_1\) bilden die beiden Katheten eines rechtwinkligen Dreiecks. Dieses Dreieck ist ein Steigungsdreieck der Sekante durch die beiden Punkte. Im Steigungsdreieck entspricht das Verhältnis \(\Delta s/\Delta t\) der Steigung der Sekante. Das Verhältnis ist mit der Definition der mittleren Geschwindigkeit identisch. Im Ort-Zeit-Diagramm erkennst du die mittlere Geschwindigkeit als Sekantensteigung.
3.4.3 Momentangeschwindigkeit im Ort-Zeit-Diagramm
Beim Übergang von der mittleren Geschwindigkeit zur Momentangeschwindigkeit haben wir auch im Ort-Zeit-Diagramm (Bild 3.23) das gleiche Problem. Sobald die Zeitpunkte \(t_1\) und \(t_2\) zusammenfallen, kann es keine Sekante im Graphen mehr geben und wir benötigen eine neue Definition. Wenn wir die Zeitintervalle immer weiter verkleinern (\(t_2\) näher an \(t_1\) rückt), kannst du erkennen, dass sich die Sekante mehr und mehr an die Tangente im Punkt \(t_1\) annähert. Die Momentangeschwindigkeit zum Zeitpunkt \(t_1\) erkennst du im Ort-Zeit-Diagramm also als Steigung der Tangente an den Graphen zu einem Zeitpunkt.
3.4.4 Interpretation von Ort-Zeit-Diagrammen
Aus der Form des Ort-Zeit-Diagramm 3.24 lässt sich einiges über die Bewegung des Körpers aussagen.
3.4.4.1 Keine Bewegung
Im Ort-Zeit-Diagramm 3.24 siehst du einige waagrechte Abschnitte, zum Beispiel in der Zeit von \(t=2\;\mathrm{s}\) bis \(t=3\;\mathrm{s}\). In diesen Abschnitten bewegt sich der Körper nicht – die Zeit vergeht, aber er bleibt immer am selben Ort.
3.4.4.2 Konstante Geschwindigkeit
In der Zeit von \(t=1\;\mathrm{s}\) bis \(t=2\;\mathrm{s}\) des Ort-Zeit-Diagramm 3.24 hat der Graph die Form einer Geraden mit positiver Steigung. Mit zunehmender Zeit wird die Ortskoordinate größer; der Körper bewegt sich vorwärts – wenn wir vorwärts mit der positiven Achsenrichtung angeben.
Auch im Abschnitt von \(t=3\;\mathrm{s}\) bis \(t=4\;\mathrm{s}\) hat die Funktion die Form einer Geraden. Diese Gerade hat aber eine negative Steigung. In so einem Fall nimmt der Ort mit fortschreitender Zeit ab – der Körper bewegt sich daher rückwärts. Hat das Ort-Zeit-Diagramm in einem Abschnitt die Form einer (geraden) Strecke, haben wir in gleichen Zeiten eine gleiche Ortsänderung. Mit der Definition der Geschwindigkeit folgt daraus, dass die Geschwindigkeit in diesen Abschnitten einen konstanten Wert hat (in waagrechten Abschnitten hat der Körper die konstante Geschwindigkeit \(v=0\)).
3.4.4.3 Konstante Beschleunigung
In der Zeit von \(t=5\;\mathrm{s}\) bis \(t=6\;\mathrm{s}\) des Ort-Zeit-Diagramm 3.24 siehst du einen Teil, in dem die Steigung des Graphen mit der Zeit immer größer wird. Die Geschwindigkeit wird also mit der Zeit immer größer. Das entspricht einer Beschleunigung. Handelt es sich dabei sogar um den Teil eines Parabel-Bogens, entspricht das einer konstanten Beschleunigung. Da der Ort größer wird, bewegt er sich wieder vorwärts.
In der Zeit \(t=7\;\mathrm{s}\) bis \(t=8\;\mathrm{s}\) findest du ebenfalls einen Teil eines Parabel-Bogens. Auch hier handelt es sich um eine konstante Beschleunigung, allerdings nimmt die Ortskoordinate ab, der Körper bewegt sich hier also rückwärts.
3.4.4.4 Allgemeine Bewegung
Im Zeitabschnitt von \(t=9\;\mathrm{s}\) bis \(t=11\;\mathrm{s}\) des Ort-Zeit-Diagramm 3.24 siehst du eine Funktion, die weder einer konstanten Geschwindigkeit (kein Abschnitt einer Geraden) noch einer konstanten Beschleunigung (kein Abschnitt einer Parabel) entspricht.
3.4.5 Geschwindigkeit-Zeit-Diagramm
In Bild 3.25 siehst du ein Beispiel für ein Geschwindigkeit-Zeit-Diagramm (engl. velocity time graph). Hier wird auf der senkrechten Achse nicht der Ort, sondern die Geschwindigkeit eines Körpers aufgetragen (ähnlich wie bei der Tachoscheibe am Kapitelanfang).
Da die Formeln von mittlerer Geschwindigkeit und mittlerer Beschleunigung sowie die Formeln von Momentangeschwindigkeit und Momentanbeschleunigung identisch aufgebaut sind, lassen sich unsere Überlegungen vom Ort-Zeit-Diagramm auf das Geschwindigkeit-Zeit-Diagramm übertragen: Die mittlere Beschleunigung ist als Steigung der Sekante in einem Punkt im Geschwindigkeit-Zeit-Diagramm erkennbar. Ebenso ist die Momentanbeschleunigung als Steigung der Tangente in einem Punkt im Geschwindigkeit-Zeit-Diagramm erkennbar.
Eine Tachoscheibe (Bild 3.20) zeigt ebenfalls ein Geschwindigkeit-Zeit-Diagramm.
3.4.6 Interpretation von Geschwindigkeit-Zeit-Diagrammen
3.4.6.1 Keine Bewegung
In einigen Abschnitten wie zum Beispiel in der Zeit von \(t=2\;\mathrm{s}\) bis \(t=3\;\mathrm{s}\) im Diagramm 3.25 hat die Funktion den konstanten Wert null. Eine Geschwindigkeit von null bedeutet, dass sich der Ort des Körpers nicht ändert – er steht für diese Zeit still.
3.4.6.2 Konstante Geschwindigkeit
In der Zeit von \(t=1\;\mathrm{s}\) bis \(t=2\;\mathrm{s}\) im Diagramm 3.25 hat die Geschwindigkeitsfunktion den konstanten Wert \(v=1\;\mathrm{m/s}\). Der positive Wert zeigt dir, dass der Ort zunimmt – der Körper bewegt sich vorwärts. Im Zeitabschnitt von \(t=3\;\mathrm{s}\) bis \(t=4\;\mathrm{s}\). In diesem Bereich ist die Geschwindigkeit zwar ebenfalls konstant, aber negativ. In diesem Fall nimmt der Ort ab – der Körper bewegt sich rückwärts.
3.4.6.3 Konstante Beschleunigung
Im Zeitintervall von \(t=5\;\mathrm{s}\) bis \(t=6\;\mathrm{s}\) im Diagramm 3.25 hat die Geschwindigkeitsfunktion eine konstante Steigung. Das ist das Kennzeichen einer konstanten Beschleunigung. Im Zeitabschnitt von \(t=7\;\mathrm{s}\) bis \(t=8\;\mathrm{s}\) siehst du ebenfalls eine konstante Beschleunigung. Das Vorzeichen der Geschwindigkeit ist hier negativ – der Körper bewegt sich (beschleunigt) rückwärts.
3.4.6.4 Allgemeine Bewegung
Im Bereich von \(t=9\;\mathrm{s}\) bis \(t=11\;\mathrm{s}\) im Diagramm 3.25 hat die Geschwindigkeitsfunktion keine konstante Steigung (weder null noch positiv oder negativ). Dort gibt es weder eine konstante Geschwindigkeit noch eine konstante Beschleunigung.
3.4.7 Zusammenhang Orts-Zeit- und Geschwindigkeits-Zeit-Diagramm
Vielleicht ist dir schon aufgefallen, dass das Ort-Zeit-Diagramm und das Geschwindigkeit-Zeit-Diagramm einer Bewegung nicht unabhängig voneinander sind. Aber da steckt noch mehr dahinter: Sie hängen nicht nur zusammen, du kannst sogar aus dem einen Diagramm, das jeweils andere rekonstruieren (Bild 3.26)!
3.4.7.1 Momentangeschwindigkeit aus dem Ort-Zeit-Diagramm bestimmen
Beginnen wir mit dem Ort-Zeit-Diagramm. Zum Zeitpunkt \(t_1\) befindet sich der Körper an einem bestimmten Ort. Die Steigung der Tangente an die Ortskurve in diesem Zeitpunkt liefert dir die Größe der Momentangeschwindigkeit zu diesem Zeitpunkt. Du findest den Wert zum selben Zeitpunkt im Geschwindigkeit-Zeit-Diagramm, wenn du dem strichlierten Ordner nach unten folgst. Warum das so sein muss, erkennst du im Steigungsdreieck der Tangente – dort findest du den Differenzenquotienten aus der Definition der mittleren Geschwindigkeit wieder.
3.4.7.2 Näherungsweise Bestimmung der Momentangeschwindigkeit aus dem Ort-Zeit-Diagramm
Statt einer Tangente kannst du auch eine Sekante durch den Punkt und einen Nachbarpunkt auf der Ortskurve verwenden. Bedenke, je kleiner das Zeitintervall der beiden Kurvenpunkte, desto genauer die Näherung für die Tangente.
3.4.7.3 Den Ort aus dem Geschwindigkeit-Zeit-Diagramm bestimmen
Betrachten wir jetzt das Geschwindigkeit-Zeit-Diagramm. Zum Zeitpunkt \(t_2\) finden wir die Momentangeschwindigkeit zu diesem Zeitpunkt eingetragen. Bilden wir die Summe der Flächeninhalte unter der Geschwindigkeitskurve, so können wir diese Summe als die Gesamt-Ortsänderung bis zu diesem Zeitpunkt interpretieren. Folge dem punktierten Ordner in das Ort-Zeit-Diagramm und du findest den entsprechenden Wert auf der Ortsachse. Beachte, dass die Flächeninhalte oberhalb der Zeitachse positiv zur Summe beitragen und Flächenteile unterhalb der Zeitachse negativ. Nur dann entspricht die Summe der Gesamt-Ortsänderung. Die Gesamt-Ortsänderung ist dabei in den meisten Fällen nicht der zurückgelegte Weg des Körpers!
3.4.7.4 Näherungsweise Bestimmung des Orts aus dem Geschwindigkeit-Zeit-Diagramm
Wenn du für die unregelmäßigen Flächen unter der Kurve den Flächeninhalt nicht berechnen kannst, gibt es die Möglichkeit, durch ein Raster aus gleich großen Quadraten oder durch rechteckige Streifen den Flächeninhalt näherungsweise zu bestimmen.
3.4.8 Mathematische Begründung durch Integral- und Differenzialrechnung
Beherrschst du schon die Differenzial- und Integralrechnung, dann erkennst du in
\[{\vec {v}}={\underset {\Delta t\rightarrow 0}{\lim }}{\frac {\Delta {\vec {s}}}{\Delta t}}={\frac {\mathrm {d} {\vec {s}}}{\mathrm {d} t}}\]
einen Differenzialquotienten. Die Steigung der Tangente und somit die Momentangeschwindigkeit erhältst du aus der Ableitung der Ortsfunktion. Umgekehrt erhältst du den Ort zu einem Zeitpunkt als bestimmtes Integral der Geschwindigkeitskurve über die Grenzen 0 und dem gesuchten Zeitpunkt (zum Beispiel \(t_2\)).
3.4.9 Zusammenhang Geschwindigkeits-Zeit- und Beschleunigungs-Zeit-Diagramm
Da die Definitionen von Momentangeschwindigkeit und Momentanbeschleunigung gleichartig aufgebaut sind, gelten die obigen Beziehungen auch zwischen Geschwindigkeit-Zeit-Diagramm und Beschleunigung-Zeit-Diagramm:
- die Tangentensteigung der Geschwindigkeitskurve liefert den Wert für die Momentanbeschleunigung.
- die Summe der Flächen unter der Kurve im Beschleunigung-Zeit-Diagramm ergibt die Gesamtänderung der Geschwindigkeit.