A.2 Cavendish-Experiment
Das nach ihm benannte Experiment wurde von Henry Cavendish um 1800 das erste Mal durchgeführt. Ziel des Experiments war es, die von Isaac Newton in seinem Gravitationsgesetz beschriebene Anziehungskraft von Massen direkt zu messen und ihre Größe zu bestimmen.
A.2.1 Idee
Die Grundlage für das Experiment ist die Torsionskraft.
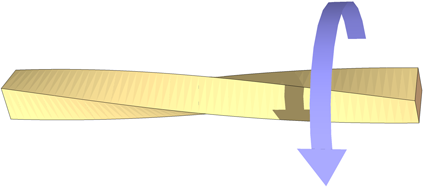
Wird ein Stab verdrillt (Bild A.6), kann aus dem Winkel seiner Verdrehung direkt auf die wirkende Kraft geschlossen werden. Der Verdrehwinkel steigt linear mit der wirkenden Kraft an.
A.2.2 Aufbau
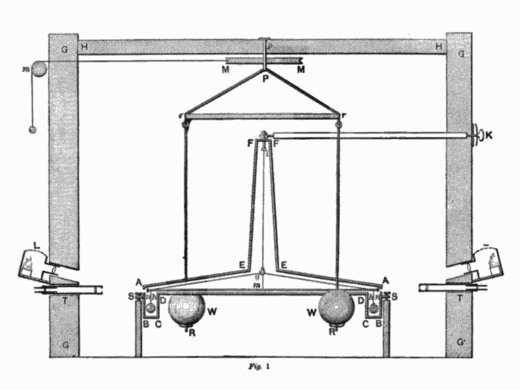
Die Drehwaage (oder Torsionswaage) besteht aus einem an einem Draht aufgehängten Stab mit zwei symmetrisch angebrachten Bleikugeln (\(m\)) an den Stabenden (Bild A.7). Werden zwei weitere Bleikugeln mit den Massen (\(M\)) hinzugefügt, wird der Draht aufgrund der Massenanziehung symmetrisch verdrillt. Aus dem Verdrehwinkel kann die Kraft berechnet werden.
Um noch so kleine Verdrehwinkel sichtbar zu machen, wird meistens auf dem Draht ein Spiegel angebracht und die Ablenkung mithilfe eines Lichtstrahls an einer entfernten Wand vergrößert (Lichtzeiger).
Links:
A.2.3 Ergebnis
Henry Cavendish gelang es als Erstem, die Gravitationskonstante mit unglaublicher Genauigkeit auf den Wert
\[ G = 6{,}67\cdot 10^{-11}\,\mathrm{\frac {m^{3}}{kg\cdot s^{2}}} \]
zu bestimmen. Mithilfe der leicht zu bestimmenden Fallbeschleunigung auf der Erdoberfläche lässt sich damit auch die Masse der Erde (\(M\)) berechnen. Setzen wir die Gravitationskraft und die Gewichtskraft für einen Körper der Masse \(m\) gleich
\[ G\cdot\frac{M\cdot m}{r^2} = m\cdot g \]
können wir aufgrund der Gleichheit von träger und schwerer Masse die Gleichung durch \(m\) dividieren und erhalten:
\[ \begin{aligned} \displaystyle g = {} & G\cdot\frac{M}{r^2} \qquad\Bigr\rvert \cdot \frac{r^2}{G}\\ M = {} & \frac{g\cdot r^2}{G} \\ \end{aligned} \]
Cavendish selbst bezeichnete das Experiment als „Wiegen der Erde“ (weighing the Earth).
A.2.4 Historische Bedeutung
Die geniale Konstruktion der Drehwaage erlaubt es, sehr kleine Kräfte zu messen. Sie wurde nicht nur erfolgreich zur Bestimmung der Größe der Gravitationskonstante verwendet, sondern lieferte auch später bei der Bestimmung der Coulombkraft von elektrisch geladenen Körpern wertvolle Ergebnisse.