A.3 Doppelspalt-Experiment von Thomas Young
In Bild A.8 siehst du eine Originalzeichnung von Thomas Young, die das Ergebnis seines um 1800 erstmals durchgeführten Doppelspalt-Versuchs dokumentiert.
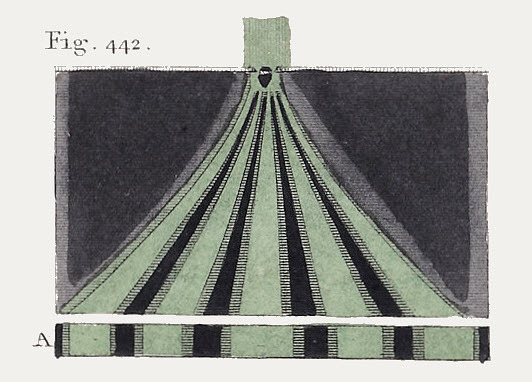
Bild A.8: Abbildung aus dem Buch „Ein Kurs von Vorlesungen über Naturphilosophie und mechanische Künste“
Im Doppelspalt-Versuch von Thomas Young geht es darum, die Wellennatur des Lichts nachzuweisen.
A.3.1 Idee
Läuft eine Wasserwelle durch einen Doppelspalt, entstehen zwei kreisförmige Elementarwellen. Überlagern sich diese, entsteht hinter dem Spalt ein deutlich sichtbares Interferenzmuster (Bild A.9).
Hat Licht Wellencharakter, sollte sich diese Interferenz auch bei Licht zeigen lassen.
A.3.2 Aufbau
In Bild A.10 siehst du den Aufbau des Doppelspalt-Experiments. Die Länge \(g\) bezeichnet den Abstand zwischen den beiden Spaltöffnungen der Blende und die Länge \(a\) den Abstand zwischen Blende und Wand.
Für die folgenden Überlegungen gehen wir davon aus, dass Abstand \(a\) sehr viel größer als der Spaltabstand \(g\) ist (\(a\gg g\)). Damit treffen die Wellenstrahlen aus beiden Spalten nahezu parallel auf der Wand auf und \(\alpha\approx\alpha'\). Außerdem nehmen wir an, dass der Spaltabstand sehr viel größer als die Wellenlänge \(\lambda\) des Lichts ist (\(d \gg \lambda\)). Beides trifft in der Praxis zu. Der Abstand zur Wand liegt in der Größenordnung von einigen Metern, der Spaltabstand in Bruchteilen von Millimetern und die Wellenlänge des Lichts in Bruchteilen von Mikrometern.
Für einen beliebigen Winkel \(\alpha\) tritt ein Gangunterschied von \(\delta\) zwischen beiden Wellenstrahlen auf, welcher als Gegenkathete im blauen Dreieck \(ABC\) zu sehen ist. Somit lässt sich die Phasenverschiebung durch den Spaltabstand \(g\) ausdrücken.
\[\begin{equation} \delta = g\cdot\sin(\alpha) \tag{A.1} \end{equation}\]
Setzen wir den Gangunterschied für konstruktive Interferenz (\(\delta = \pm n\cdot\lambda\)) ein, erhalten wir die Bedingung für Winkel maximaler Helligkeit:
| \[ \pm n\cdot\lambda = g\cdot\sin(\alpha), \qquad n=0,1,2,3,\ldots \tag{A.2} \] |
Für \(n=0\) folgt \(\alpha=0\) und das Maximum befindet sich exakt in der Mitte. Es wird Maximum nullter Ordnung genannt. Links und rechts davon befinden sich jeweils im gleichen Abstand die Maxima erster Ordnung (\(n=\pm1\)), Maxima zweiter Ordnung (\(n=\pm2\)) und so weiter.
Setzen wir stattdessen den Gangunterschied für destruktive Interferenz (\(\delta = \pm (n+\frac{1}{2})\cdot\lambda\)) ein, erhalten wir die Bedingung für Winkel minimaler Helligkeit (dunkle Stellen):
| \[ \pm (n+\frac{1}{2})\cdot\lambda\ = g\cdot\sin(\alpha), \qquad n=0,1,2,3,\ldots \tag{A.3} \] |
Der Abstand zwischen den Stellen maximaler Helligkeit an der Wand (ebenso wie den Stellen minimaler Helligkeit) hängt von der Wellenlänge \(\lambda\) des Lichts ab. Für den Winkel zwischen den Maxima nullter und erster Ordnung gilt:
\[\begin{equation} \lambda = g\cdot\sin(\alpha) \tag{A.4} \end{equation}\]
Für kleine Winkel \(\alpha\) gilt die Näherung \(\sin(\alpha)\approx\tan(\alpha)\). Damit können wir den Sinus durch das Verhältnis von Entfernung \(d_{01}\) zwischen Maximum nullter und erster Ordnung am Schirm und der Entfernung \(a\) (Abstand Blende-Schirm) ausdrücken. Aus dem grünen rechtwinkeligen Dreieck \(M'MP\) folgt für den Tangens:
\[ \sin(\alpha)\approx\tan(\alpha)=\frac{d_{01}}{a} \]
Setzen wir das Verhältnis in Gleichung (A.4) ein, folgt für die Wellenlänge:
\[\begin{equation} \lambda = g\cdot\frac{d_{01}}{a} \tag{A.5} \end{equation}\]
Mithilfe dieser einfachen Gleichung können wir die Wellenlänge des verwendeten Lichts berechnen, obwohl diese viele Größenordnungen unter denen der anderen Längen liegt!
A.3.3 Ergebnis
Als Thomas Young um 1800 das erste Mal durchführte, war am Auffangschirm ein deutliches Interferenzmuster zu sehen (Bild A.11). Er verwendete aber keine monochromatische Lichtquelle, sondern die Sonne. Damit ergeben sich für die einzelnen Wellenlängen (Farben) unterschiedliche Abstände zwischen den Maxima und Minima (Beugungsspektrum).
Interferenz zeigt sich allerdings nur bei kohärentem Licht. Um kohärentes Licht aus dem Sonnenlicht zu gewinnen, platzierte Thomas Young vor dem Doppelspalt noch einen Einzelspalt. Die Wellenfronten der am Einzelspalt erzeugten Kreiswelle treffen auf die beiden Spalte und regen dort zwei gleichphasige Kreiswellen an.
A.3.4 Historische Bedeutung
Isaac Newton interessierte sich schon in jungen Jahren für die Natur des Lichts (Bild A.12). Da sich Licht in seinen Experimenten geradlinig ausbreitete, vermutete er, dass Licht aus winzigen Lichtteilchen besteht. Nach seiner Vorstellung bewegen sich diese Lichtteilchen mit endlicher Geschwindigkeit und wechselwirken mit ihrer Umgebung (zum Beispiel mit einem Spiegel oder dem Auge) nach den Gesetzen der newtonschen Physik. Aufgrund des enormen Ansehens Newtons setzte sich das Teilchenmodell von Licht bald allgemein durch.
Obwohl bereits Zeitgenossen Newtons, unter ihnen Robert Hooke und Christiaan Huygens, vermuteten, dass es sich bei Licht um eine Welle handelt, sollte es noch rund hundert Jahre dauern, bis Thomas Young den Wellencharakter durch sein Doppelspalt-Experiment eindeutig zeigte. Aber nicht nur das: Mithilfe der Gleichung (A.5) gelang es ihm sogar, die Größenordnung der Lichtwellenlängen aus den Abständen der Maxima zu bestimmen. Damit setzte sich das Wellenmodell des Lichts Anfang des 19. Jahrhunderts schließlich durch. Mit dem Aufkommen der Quantenmechanik Anfang des 20. Jahrhunderts änderte sich allerdings unsere Vorstellung von der Natur des Lichts erneut.





